【策略】UVa 278 - Chess
| Chess |
Almost everyone knows the problem of putting eight queens on an chessboard such that no Queen can take another Queen. Jan Timman (a famous Dutch chessplayer) wants to know the maximum number of chesspieces of one kind which can be put on an board with a certain size such that no piece can take another. Because it's rather difficult to find a solution by hand, he asks your help to solve the problem.
He doesn't need to know the answer for every piece. Pawns seems rather uninteresting and he doesn't like Bishops anyway. He only wants to know how many Rooks, Knights, Queens or Kings can be placed on one board, such that one piece can't take any other.
Input
The first line of input contains the number of problems. A problem is stated on one line and consists of one character from the following set r, k, Q, K, meaning respectively the chesspieces Rook, Knight, Queen or King. The character is followed by the integers m ( ) and n ( ), meaning the number of rows and the number of columns or the board.
Output
For each problem specification in the input your program should output the maximum number of chesspieces which can be put on a board with the given formats so they are not in position to take any other piece.
Note: The bottom left square is 1, 1.
Sample Input
2 r 6 7 k 8 8
Sample Output
6 32
题意:在一个m*n的棋盘上最多能放置多少个c类型的棋子。棋子间保证不互相攻击。
攻击方式为国际象棋规则,首先简单科普一下:
Q(Queen):按照八皇后攻击规则,即一行,一列,对角线不能存在棋子。可知最多能放八个棋子。
K(King):国王攻击周围八个棋子。最优方案为行列间隔放置。
r (Rook):战车攻击方式为直线攻击。所以最多能放行列的最小值。
k(Knight):骑士的攻击方式为日字攻击,但不会“蹩马腿”。骑士的方案需要分情况:
1、当只有一行(列)时,当然可以放全部棋子。
2、当有两行(列)时,最优方案时田字放置。盗图一张。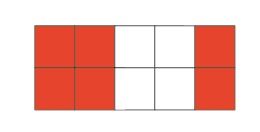 、
、
3、当大于两行(列)时,最优方案是隔列放置。
附代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #define error 1e-8 6 using namespace std; 7 const int maxn = 15; 8 int chess[maxn][maxn]; 9 int main() 10 { 11 int T; scanf("%d", &T); 12 while(T--) 13 { 14 char kind[2]; int r, c; 15 int ans; 16 scanf("%s%d%d", kind, &r, &c); 17 if(kind[0] == 'r' || kind[0] == 'Q') ans = min(r, c); 18 else if(kind[0] == 'K') 19 { 20 ans = ((r+1)/2)*((c+1)/2); 21 } 22 else if(kind[0] == 'k') 23 { 24 int m = max(r, c), n = min(r, c); 25 if(r == 1 || c == 1) ans = m; 26 else if(r == 2 || c == 2) 27 { 28 ans = m/2*2 + m%2*2; 29 } 30 else 31 { 32 ans = (n/2)*(m/2+(m+1)/2) + (n%2)*((m+1)/2); 33 } 34 } 35 printf("%d\n", ans); 36 } 37 return 0; 38 }
