本系列是台湾大学资讯工程系林軒田(Hsuan-Tien Lin)教授开设的《机器学习基石》课程的梳理。重在梳理,而非详细的笔记,因此可能会略去一些细节。
该课程共16讲,分为4个部分:
- 机器什么时候能够学习?(When Can Machines Learn?)
- 机器为什么能够学习?(Why Can Machines Learn?)
- 机器怎样学习?(How Can Machines Learn?)
- 机器怎样可以学得更好?(How Can Machines Learn Better?)
本文是第3部分,对应原课程中的9-12讲。
本部分的主要内容:
- 线性回归算法详解,以及泛化能力的保证、能否用于二分类问题等;
- 逻辑回归算法详解,并引入梯度下降方法;
- 阐述PLA、线性回归、逻辑回归3种方法在分类问题上的联系与区别,并引入随机梯度下降方法;
- 多分类问题中的OVA、OVO方法;
- 特征的非线性变换,以及该如何控制变换后的复杂度。
1 线性回归
在第一部分中讲过机器学习的分类,当\(\mathcal{Y}=\mathbb{R}\)时,就是回归。
1.1 线性回归算法
线性回归的假设集十分简单,\(h(\mathbf{x})=\mathbf{w}^T\mathbf{x}\),其实就是感知机模型去除了符号函数。
它的逐点误差度量可设为\(\text{err}(\hat{y}, y)=(\hat{y}-y)^2\),那么样本内外的误差分别为
和
要最小化\(E_{\text{in}}\)很简单,当它取到最小时必有梯度为\(0\),因此可先计算出它的梯度:
令它为\(0\)即可。如图所示:
若\(X^T X\)可逆(当\(N\gg d+1\)时基本上会满足),则可直接得出
如果\(X^T X\)是奇异的呢?可先定义“伪逆”(pseudo-inverse)\(X^\dagger\),在定义完后有
在实践中,建议直接使用\(X^\dagger\),一方面可避免判断\(X^T X\)是否可逆,另一方面就算在几乎不可逆的情况下,它也是在数值上稳定的。
1.2 线性回归的泛化
线性回归看起来没有“学习”过程,是一步到位的,那么它算机器学习吗?
事实上,只要可以保证\(E_{\text{out}}(\mathbf{w}_\text{LIN})\)足够小,那么就可以说“发生了”学习。
在这里,我们不从VC维理论出发,而从另一个角度说明为什么\(E_{\text{out}}(\mathbf{w}_\text{LIN})\)会足够小。
我们先来看平均的\(E_{\text{in}}\)有多大:
其中
可将\(H=XX^\dagger\)称为hat matrix,因为它可将\(\mathbf{y}\)映射到\(\hat{\mathbf{y}}\)。由下图可知,若\(\mathbf{y}\)由理想的\(f(X)\in \text{span}\)加上噪声\(\mathbf{noise}\)生成,那么\(I-H\)也可将\(\mathbf{noise}\)映射为\(\mathbf{y}-\hat{\mathbf{y}}\):
而\(\text{trace}(I-H)=N-(d+1)\),迹可以理解为“能量”,因此有
如果对\(E_{\text{in}}\)取平均,大概可以理解为
类似地有
(证明过程略)。
因此\(\overline{E_{\text{in}}}\)和\(\overline{E_{\text{out}}}\)的关系如图:
若\(N\to\infty\),则二者都收敛于\(\sigma^2\)(\(\mathbf{noise}\text{ level}\)),泛化误差的期望为\(\dfrac{2(d+1)}{N}\)。因此,学习是会“发生”的!
VC维理论说明的是\(E_{\text{in}}\)和\(E_{\text{out}}\)相差较远的概率有上限,而这里说明的是它们的平均差距会收敛。角度不同,但两种方式都说明了泛化的能力。
1.3 用线性回归进行二分类
在线性分类中,\(\mathcal{Y}=\{+1,-1\}\),\(h(\mathbf{x})=\text{sign}({\mathbf{w}^T\mathbf{x}})\),\(\text{err}(\hat{y},y)=\mathbf{1}_{[\hat{y}\ne y]}\),找它的最优解是个NP-hard问题。
由于\(\{+1,-1\}\subset \mathbb{R}\),即样本的正负类别也能用实数表示,而在线性回归中\(\mathcal{Y}=\mathbb{R}\),那么,直接来一发线性回归,得到\(\mathbf{w}_\text{LIN}\),然后让\(g(\mathbf{x})=\text{sign}(\mathbf{w}_\text{LIN}^T\mathbf{x})\),这是否可行呢?
把线性分类和线性回归的误差度量分别记为\(\text{err}_{0/1}=\mathbf{1}_{[\text{sign}(\mathbf{w}^T\mathbf{x})\ne y]}\)和\(\text{err}_\text{sqr}=({\mathbf{w}^T\mathbf{x}- y})^2\),它们的关系如下图:
从中可直观地看出,\(\text{err}_{0/1} \le \text{err}_\text{sqr}\)一定成立。由此,有
也就是说,让回归的\(E_{\text{in}}\)做得足够好,也可以使得分类的\(E_{\text{out}}\)足够小,只不过上限更宽松一些而已。这样做就是用边界的紧度(bound tightness)换取计算效率(efficiency)。
一般\(\mathbf{w}_\text{LIN}\)可用来作为PLA或pocket算法的初始向量。
2 逻辑回归
2.1 逻辑回归算法
二分类中,我们感兴趣的是
但在很多场景下,我们想要做的是“软”(soft)分类,即得到某个分类的概率,此时感兴趣的是
问题在于,我们得到的数据标签是样本的类别,而非样本被分到某个类的概率。
对于一个样本的所有特征\(\mathbf{x}=(x_0, x_1, x_2, \cdots,x_d)\),令\(s=\sum\limits_{i=0}^{d} w_i x_i\)。我们可用逻辑函数(logistic function)\(\theta(s)\)将它转换成估计的概率。也就是说,逻辑回归(logistic regression)的假设为\(h(\mathbf{x})=\theta(\mathbf{w}^T\mathbf{x})\)。
最常用的逻辑函数是
函数图像如下:
可见,它是个光滑的、单调的、“S”形的(sigmoid)函数。
接下来,要定义逻辑回归的\(E_\text{in}(\mathbf{w})\)。先将目标函数\(f(\mathbf{x})=P(+1|\mathbf{x})\)反表示为
假设手中的数据集为
那么,由\(f\)生成\(\mathcal{D}\)的概率为
由我们的假设\(h\)生成\(\mathcal{D}\)的似然(likelihood)为
如果\(h\approx f\),那么\(h\)生成\(\mathcal{D}\)的似然也应该接近于由\(f\)生成\(\mathcal{D}\)的概率,并且由\(f\)生成\(\mathcal{D}\)的概率应该是较大的(正好被我们抽样抽到)。所以,机器学习算法可以取
若\(h(\mathbf{x})=\theta(\mathbf{w}^T\mathbf{x})\),由函数的性质可知,\(1-h(\mathbf{x})=h(-\mathbf{x})\),所以
而\(P(\mathbf{x}_1)\)、\(P(\mathbf{x}_2)\)、……、\(P(\mathbf{x}_N)\)都与\(h\)无关,因此有
现在要将它最大化,以找出最终的\(h\)。可先把\(\theta(s)\)代入,再取对数(对数函数单调,不改变最大化取值的点),变为
再取相反数(最大化变为最小化)、除\(N\)(不改变最值点)后,又可变为
将\(\theta(s)\)展开得到
令
这就是交叉熵误差(cross-entropy error),而\(\sum\limits_{n=1}^N \text{err}(\mathbf{w},\mathbf{x}_n,y_n)\)就是\(E_\text{in}(\mathbf{w})\)。
2.2 梯度下降
接下来就要最小化\(E_\text{in}(\mathbf{w})\),它是连续的、可微的、二次可微的、凸的,因此可以试着让它梯度为\(0\)。求出它的梯度
它的梯度可以看成是以\(\theta(\cdot)\)为权重的\(-y_n\mathbf{x}_n\)的加权平均。要让它为0,有两种方式:
- 让所有的\(\theta(-y_n\mathbf{w}^T\mathbf{x}_n)\)都为0,这意味着所有样本都满足\(y_n\mathbf{w}_n\mathbf{x}_n\gg 0\),也即\(\mathcal{D}\)是线性可分的;
- 若\(\mathcal{D}\)不是线性可分的,要让加权和为0,这是个非线性方程,没有闭式解(closed-form solution)。
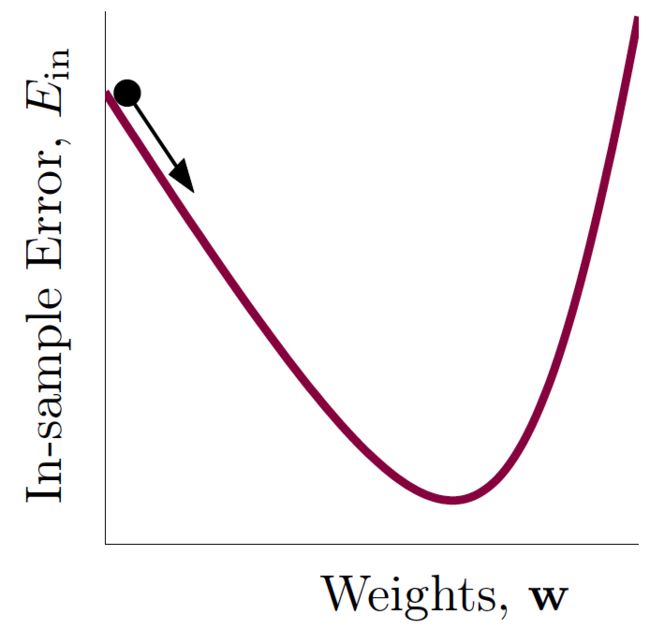
可用与PLA中类似的方法进行迭代,即\(\mathbf{w}_{t+1}\leftarrow\mathbf{w}_t+\eta\mathbf{v}\),其中\(\mathbf{v}\)确定了更新的方向,\(\eta\)确定了更新的步长,如图:
怎么迭代呢?可用贪心算法,一步步让\(E_\text{in}\)变小。假设已经给定某个\(\eta\),要确定\(\mathbf{v}\)的方向,每一步的更新问题就转换成了
看起来仿佛更难解了。但如果\(\eta\)足够小,我们可以用局部线性近似展开它(泰勒展开,Taylor expansion):
式中\(E_\text{in}(\mathbf{w}_t)\)和\(\nabla E_\text{in}(\mathbf{w}_t)\)已知,\(\eta\)给定,只需确定\(\mathbf{v}\)即可,注意到上式第二项本质上是两个向量内积,当两个向量方向相反时值最小,因此要最小化上式,可取
梯度下降的迭代更新就变成了:对于给定的较小\(\eta\),
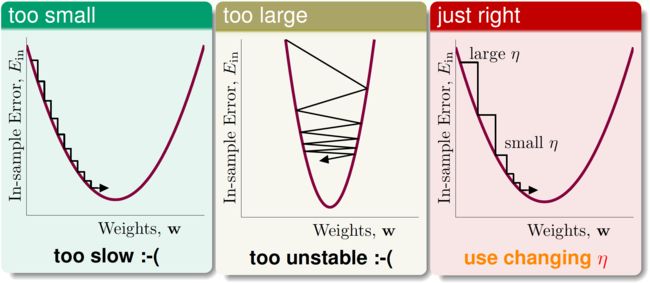
\(\eta\)太小会导致非常慢,太大会导致不稳定,最好用变化的\(\eta\),如下图所示:
那么,\(\eta\)怎么变比较好?可让它与\(\Vert\nabla E_\text{in}(\mathbf{w}_t)\Vert\)正相关,将原来固定的\(\eta\)乘上\(\Vert\nabla E_\text{in}(\mathbf{w}_t)\Vert\)即可。这样,更新规则也就变成了
这个新的\(\eta\)可叫作固定的学习率(learning rate)。
3 分类的线性模型
3.1 三种算法的比较
记\(s=\mathbf{w}^T\mathbf{x}\),以下是总结三种模型(线性分类、线性回归、逻辑回归):
这里的\(ys\)可称为分类正确度分数(classification correctness score),即度量分类有多正确,该值越大,说明分类越“正确”。
若将交叉熵误差函数\(\text{err}_\text{CE}(s,y)\)做scale(除\(\ln 2\)),得到
把它们的误差函数都画出来,可得下图:
从图中可知,一定有
由此可以用VC维理论证明,使用\(\text{err}_\text{CE}\)也可以做好分类任务,有两种思路:
- 从分类的角度出发,有
- 从交叉熵角度出发,有
不管用哪种方式,只要保证\(E_\text{in}^\text{CE}\)足够小,都可以保证\(E_\text{out}^{0/1}(\mathbf{w})\)也足够小,也就是说,使用逻辑回归或线性回归都可以做线性分类。
用PLA、线性回归、逻辑回归做分类,三种方法的优缺点如下:
3.2 随机梯度下降
PLA每次迭代的时间复杂度为\(O(1)\),但逻辑回归(或pocket算法)每次迭代都需要对\(\mathcal{D}\)中的所有样本进行一次运算,时间复杂度为\(O(N)\),能不能让每次迭代的时间复杂度也变成\(O(1)\)?
我们在做更新\(\mathbf{w}_{t+1}\leftarrow\mathbf{w}_t+\eta\mathbf{v}\)时,取了
可以看到,计算梯度需要遍历所有样本,复杂度实在太高了。可将它里面的\(\dfrac{1}{N}\sum\limits_{n=1}^{N}\)看作是期望\(\mathcal{E}\),相当于不断随机抽一个样本计算出来的结果的平均。若将随机抽一个样本\(n\)算出来的梯度称为随机梯度\(\nabla_\mathbf{w}\text{err}(\mathbf{w},\mathbf{x}_n,y_n)\),那么真正的梯度可看作是它的期望:
这样,就可以用随机梯度下降(Stochastic Gradient Descent,SGD)进行迭代。它的好处是非常简单,计算的成本低,非常适用于大数据或在线学习的情况,缺点是不够稳定。
在逻辑回归中,用SGD更新的步骤就变成了
这与PLA中的更新步骤十分相似,PLA中是这样的:
因此用SGD的逻辑回归,可以看作是“软”的PLA。而反过来,若取\(\eta=1\),则PLA在\(\mathbf{w}_t^T \mathbf{x}_n\)很大的时候也可以看作是用SGD的逻辑回归。
在用SGD时,有两个经验法则:
- 什么时候停止?\(t\)足够大的时候就可以(不要判断梯度是否真的为0,否则又会带来梯度计算的复杂度);
- 当\(\mathbf{x}\)在一般范围内时,就取\(\eta=0.1\)吧。
4 多分类问题
4.1 用逻辑回归做多分类
假设\(\mathcal{Y}=\{\square, \diamondsuit,\triangle,\star\}\),数据分布如下图:
可对每个类别分别做一次分类,如下图:
但这样做,在最后要把它们结合起来时,会出现问题,有些区域无法判定属于哪一类:
怎么解决呢?可以用逻辑回归做“软”分类器,依旧是对每个类别\(k\),用数据集
做一次逻辑回归,得到一个分类器\(\mathbf{w}_{[k]}\):
做完后要将它们结合起来,可取\(g(\mathbf{x})=\arg\max_{k\in\mathcal{Y}}\theta(\mathbf{w}_{[k]}^T\mathbf{x})\),这样就得到某个点应该属于哪一类了:
这样做称为OVA(One-Versus-All) Decomposition,好处是有效率,可以和类似逻辑回归的方法结合起来,但缺点在于当\(K\)很大时,往往会使\(\mathcal{D}_{[k]}\)非常不平衡,比如有100类,并且分布比较均匀,OVA每次用于训练的样本的两类数据的个数就会非常悬殊。
可以再进行扩展,如multinomial ('coupled') logistic regression,加入一些如“属于不同类的概率加起来应该为1”之类的限制,让它更适合用于多分类。
4.2 用二分类做多分类
为了克服不平衡问题,可以对两两类别进行训练,即用数据集
进行线性二分类:
最后,取
即可:
这样的方法叫作OVO(One-Versus-One)Decomposition,好处在于有效率(因为每次训练用的数据量较少),并且是稳定的,可以和任何二分类方法相结合,但缺点在于不断计算\(\mathbf{w}_{[k,\ell]}\)的操作总共的复杂度是\(O(K^2)\),需要更多运算空间。当\(K\)不是非常大时,OVO很常用。
5 非线性变换
对于某些数据集来说,不管怎么使用线性模型,\(E_{in}\)都很大:
5.1 二次的假设集
我们发现,如果用一个圆来做它的分类界线,它其实是可分的:
所以我们要重新设计圆形PLA、圆形回归、……吗?当然不是。我们可以将\(\mathbf{x}\in\mathcal{X}\)用变换\(\Phi\)映射到\(\mathbf{z}\in\mathcal{Z}\),使得在\(\mathcal{X}\)中圆形可分的数据在\(\mathcal{Z}\)中线性可分。
通过由\(\Phi_2(\mathbf{x})=(1,x_1,x_2,x_1^2,x_1x_2,x^2_2)\)映射而来的\(\mathcal{Z}\)空间,可构成一般的二次假设集:
当然也可以用更高次的非线性变换,用非线性变换的流程如下图:
具体步骤如下:
- 先用\(\Phi\)将\(\{(\mathbf{x}_n,y_n)\}\)变换到\(\{(\mathbf{z}_n=\Phi(\mathbf{x}_n),y_n)\}\);
- 用\(\{(\mathbf{z}_n,y_n)\}\)和线性分类算法\(\mathcal{A}\)训练出模型\(\tilde{\mathbf{w}}\);
- 返回\(g(\mathbf{x})=\text{sign}\left(\tilde{\mathbf{w}}^T \Phi(\mathbf{x})\right)\)即可。
5.2 复杂度的代价
假设用\(Q\)次的非线性变换:
式中的项数\(1+\tilde d\)是多少呢?若有\(d\)个特征,可以在补上1后认为上面式子后边的每一项都是\(Q\)次的,也就是说要对\(d+1\)项每项都赋予一个次数,并且所有次数之和必须为\(Q\)。可以用隔板法:想象共有\(Q+d+1\)个小球,要在它们的空隙中放入\(d\)个隔板,隔成\(d+1\)段,每一段的小球个数减去1代表了对应位置的项的次数,由于要求每段中至少有1个小球,因此两端不能放隔板,共有\(Q+d\)个位置可放隔板,共有\(\binom{Q+d}{d}\)种放法,也就是说,上式等号右边的项数
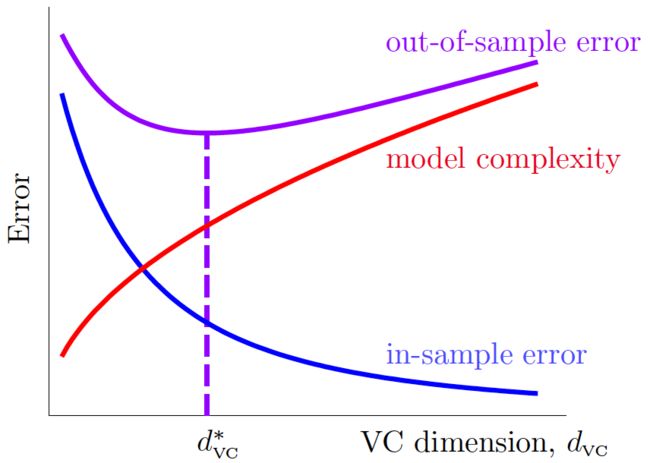
当\(Q\)较大时,一方面计算或存储的成本非常高,另一方面\(1+\tilde d\)是\(d_\text{VC}(\mathcal{H}_{\Phi_Q})\)的上界,\(Q\)太大会导致\(d_\text{VC}\)过大,模型损失了泛化能力。
5.3 \(Q\)的选择
如何选择\(Q\)?假设\(\Phi_0(\mathbf{x})=(1)\),\(\Phi_1(\mathbf{x})=\left(\Phi_0(\mathbf{x}),x_1,x_2,\ldots,x_d,\right)\),……,\(\Phi_Q(\mathbf{x})=\left(\Phi_{Q-1}(\mathbf{x}),x_1^Q,x_1^{Q-1}x_2,\ldots,x_d^Q,\right)\),将它们的假设集分别记为\(\mathcal{H}_0\),\(\mathcal{H}_1\),……,\(\mathcal{H}_Q\),它们存在嵌套关系
如图所示:
并且,它们的VC维满足
若取\(g_i=\arg\min_{h\in \mathcal{H}_i} E_\text{in}(h)\),则它们的\(E_\text{in}\)满足
如何选择\(Q\)?安全的做法是,先看\(E_\text{in}(g_1)\)是否已经足够小,如果足够小,就可以了,否则,就用再稍微复杂一些的模型,也就是在下图中向右移动: