3D库WxGL的demo——用3D给思维插上想象的翅膀
文章目录
- 1 前言
- 2 正弦曲线 y = s i n x y=sinx y=sinx
- 3 最简单的曲面 z = x y z=xy z=xy
- 4 稍微有点难度的曲面 z = s i n ( x ) + c o s ( y ) z=sin(x)+cos(y) z=sin(x)+cos(y)
- 5 无法凭空想象的曲面 z = 2 x e x 2 + y 2 z=\frac{2x}{e^{x^2+y^2}} z=ex2+y22x
- 6 体数据 s i n ( x ) + s i n ( y ) + s i n ( z ) sin(x)+sin(y)+sin(z) sin(x)+sin(y)+sin(z)
- 7 球和六面体的组合
- 8 地球
- 9 三维重建
1 前言
上周冒着零星小雨去附近的公园赏花,估计脑子里多少进了一些雨水,以至于连 z = x y z=xy z=xy 这样的曲面是什么样子,都想象不出来了。无奈之下,只好跑去问女儿。彼时,她正在ipad上整理课堂笔记。我凑近瞄了一眼,瞬间感觉头晕目眩,几乎晕倒。这个课堂笔记,将数学的险恶展示得一览无余!

听完我的问题,女儿笑了:用一方手帕表示这个曲面,手帕的左下角、右上角高高提起,左上角、右下角自然垂落,大概就是 z = x y z=xy z=xy 的样子。 x x x y y y同号则 z z z大于零,异号则 z z z小于零,这么简单的问题,你都搞不懂,脑子是不是进水了?
天哪,脑子进水这事儿,居然被她猜到了!
“别乱说,下雨那天我打伞了。”
我一边小声反驳着,一边落荒式地逃离了女儿的房间。
这事儿虽然有损于我在女儿心目中的光辉象形,倒也反映了一个事实:有些看似简单的数学方程,却可以构造出极其复杂的曲面或几何体,如果没有3D工具的辅助,即便脑子没有进水,人类也很难凭空想象出它的样子。另外,在学习或研究过程中,我们关注的数据往往会藏身于茫茫“数海”中,如果不借助于3D技术,我们很难想象它们是什么样子的,又是如何分布的。
WxGL正是这样一个用于应对上述需求的3D数据可视化工具,可以很方便地画一些点面线体及其组合。关于WxGL,更多的信息请参考《开源我的3D库WxGL:40行代码将疫情地图变成三维地球模型》。WxGL最初是我们的开发团队自用的小工具,所以开源以后既没有像样的文档,也没有简单的例子。本文就算是开源3D库WxGL的demo吧,全部应用实例集成在一个脚本中,同时增加了3D系统信息显示和位置姿态设置。本文仅对部分代码做解读,并没有提供完整源码。源码已经更新到了GitHub,感兴趣的同学可以去下载。

2 正弦曲线 y = s i n x y=sinx y=sinx
绘制 x x x o o o y y y平面上的正弦曲线,首先要约定 x x x的值域范围,从中(等距离)取出一定数量的点,计算各点对应的 y y y值。不用说,每个点对应的 z z z值一定是零。将各点 x x x、 y y y、 z z z拼合成顶点集 v v v,颜色集 c c c用 y y y的大小做映射,用drawLine()就可以轻松画出正弦曲线了。
x = np.linspace(-2*np.pi, 2*np.pi, 1000)
y = np.sin(x)
z = np.zeros(1000)
v = np.dstack((x,y,z))[0]
c = self.cm.map(y, self.cm_curr, mode='RGBA')
self.master.drawLine('sin', v, c, method='SINGLE')
self.master.update()
3 最简单的曲面 z = x y z=xy z=xy
x x x在 [ − 1 , 1 ] [-1, 1] [−1,1]之间均匀取51个点, y y y在 [ − 1 , 1 ] [-1, 1] [−1,1]之间均匀取51个点,生成 x x x和 y y y的网格,分别计算网格上每个点的 x x x和 y y y的积作为 z z z,颜色集 c c c用 z z z的大小做映射,用drawMesh()绘制网格。
y, x = np.mgrid[-1:1:51j, -1:1:51j]
z = x*y
c = self.cm.map(z, self.cm_curr, mode='RGBA')
self.master.drawMesh('z=xy', x, y, z, c, mode=self.render)
self.master.update()
下图使用了“前面显示线条后面填充颜色”渲染效果。如果两面都使用颜色或者线条,视觉效果会比较平淡。

4 稍微有点难度的曲面 z = s i n ( x ) + c o s ( y ) z=sin(x)+cos(y) z=sin(x)+cos(y)
x x x在 [ − π , π ] [-\pi,\pi] [−π,π]之间均匀取51个点, y y y在 [ − π , π ] [-\pi,\pi] [−π,π]之间均匀取51个点,生成 x x x和 y y y的网格,分别计算网格上每个点的 s i n ( x ) sin(x) sin(x)和 c o s ( y ) cos(y) cos(y)的和作为 z z z,颜色集 c c c用 z z z的大小做映射,用drawMesh()绘制网格。
y, x = np.mgrid[-np.pi:np.pi:51j, -np.pi:np.pi:51j]
z = np.sin(x) + np.cos(y)
c = self.cm.map(z, self.cm_curr, mode='RGBA')
self.master.drawMesh('z=xy', x, y, z, c, mode=self.render)
self.master.update()
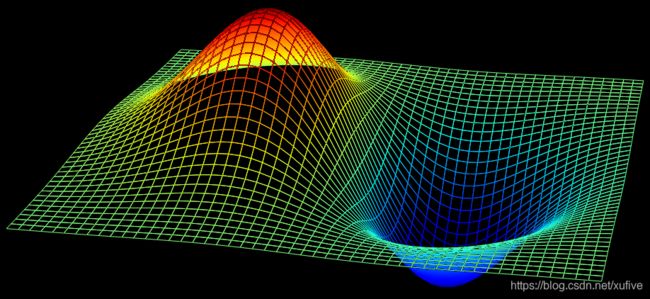
5 无法凭空想象的曲面 z = 2 x e x 2 + y 2 z=\frac{2x}{e^{x^2+y^2}} z=ex2+y22x
x x x在 [ − 1 , 1 ] [-1, 1] [−1,1]之间均匀取51个点, y y y在 [ − 1 , 1 ] [-1, 1] [−1,1]之间均匀取51个点,生成 x x x和 y y y的网格,分别计算网格上每个点的 2 x e x 2 + y 2 \frac{2x}{e^{x^2+y^2}} ex2+y22x作为 z z z,颜色集 c c c用 z z z的大小做映射,用drawMesh()绘制网格。
x, y = np.mgrid[-2:2:50j,-2:2:50j]
z = 2*x*np.exp(-x**2-y**2)
c = self.cm.map(z, self.cm_curr, mode='RGBA')
self.master.drawMesh('z=xy', x, y, z, c, mode=self.render)
self.master.update()
下图使用了“前面填充颜色后面显示线条”渲染效果:
 换个角度,换个ColorMap,看看效果:
换个角度,换个ColorMap,看看效果:
两面全用颜色试一试:

6 体数据 s i n ( x ) + s i n ( y ) + s i n ( z ) sin(x)+sin(y)+sin(z) sin(x)+sin(y)+sin(z)
对于空间中的一个点,其坐标为 ( x , y , z ) (x,y,z) (x,y,z),如果将 s i n ( x ) + s i n ( y ) + s i n ( z ) sin(x)+sin(y)+sin(z) sin(x)+sin(y)+sin(z) 映射为该点的颜色,则该颜色集就可以成为体数据。
y, x = np.mgrid[-10:10:101j, -10:10:101j]
z = np.linspace(-10, 10, 101)
v = np.sin(z).repeat(101*101).reshape((101,101,101)) + np.sin(x) + np.sin(y)
c = self.cm.map(v, self.cm_curr, mode='RGBA')
self.master.drawVolume('volume', c, x, y, z, smooth=False)
self.master.update()
这是以原点为中心的 20 × 20 × 20 20\times20\times20 20×20×20 的立方体,每一个点的颜色和 s i n ( x ) + s i n ( y ) + s i n ( z ) sin(x)+sin(y)+sin(z) sin(x)+sin(y)+sin(z) 的对应关系如ColorBar所示。

但是,很多时候,我们更关心在这数据体内,某一类数据,比如说 s i n ( x ) + s i n ( y ) + s i n ( z ) = 0 sin(x)+sin(y)+sin(z)=0 sin(x)+sin(y)+sin(z)=0 的点有哪些?又是如何分布的呢?很简单,我们只需要把这些点之外的其他点的颜色的透明度置为零,我们在视觉上就只会看到 s i n ( x ) + s i n ( y ) + s i n ( z ) = 0 sin(x)+sin(y)+sin(z)=0 sin(x)+sin(y)+sin(z)=0 的点了。
c = self.cm.map(np.where((v>-0.1)&(v<0.1), v, np.nan), self.cm_curr, mode='RGBA')
由于我们在空间中的选取的点不是连续的,因此,我们把 s i n ( x ) + s i n ( y ) + s i n ( z ) = 0 sin(x)+sin(y)+sin(z)=0 sin(x)+sin(y)+sin(z)=0 的条件改为 − 0.5 < s i n ( x ) + s i n ( y ) + s i n ( z ) < 0.5 -0.5

被剔除的另一部分是这样的:

如果把筛选条件改为 − 0.1 < s i n ( x ) + s i n ( y ) + s i n ( z ) < 0.1 -0.1

如果把筛选条件改为 − 0.01 < s i n ( x ) + s i n ( y ) + s i n ( z ) < 0.01 -0.01

7 球和六面体的组合
在三维空间中生成一个球体表面上各个点的坐标,需要借助于参数方程。我们可以借助于地球的经纬度概念,按照固定步长,经度从-180°变化到到180°,维度从-90变化到°到90°,就得到了经度和维度网格:
lat, lon = np.mgrid[-0.5*np.pi:0.5*np.pi:51j, -np.pi:np.pi:101j]
根据球体表面上每个点的经度纬度,很容易计算出每个点的空间坐标:
z = np.sin(lat)
x = np.cos(lat)*np.cos(lon)
y = np.cos(lat)*np.sin(lon)
为了让球体表面颜色漂亮一点,我们用每一点上 x x x和 y y y的乘积映射颜色:
c = self.cm.map(x*y, self.cm_curr, mode='RGBA')
使用drawMesh()画出这个网格:
self.master.drawMesh('ball', x, y, z, c=c, mode=self.render)
六面体相对简单一些,我们可以分开画六个面,每个面的颜色随机生成:
v0, v1, v2, v3 = [1,1,-1], [-1,1,-1], [-1,-1,-1], [1,-1,-1]
v4, v5, v6, v7 = [1,1,1], [-1,1,1], [-1,-1,1], [1,-1,1]
bottom = np.array([v0, v3, v2, v1])*0.75
top = np.array([v4, v5, v6, v7])*0.75
front = np.array([v7, v6, v2, v3])*0.75
back = np.array([v4, v0, v1, v5])*0.75
right = np.array([v4, v7, v3, v0])*0.75
left = np.array([v6, v5, v1, v2])*0.75
self.master.drawSurface('cubo', bottom, c=np.random.random(3), mode=self.render)
self.master.drawSurface('cubo', top, c=np.random.random(3), mode=self.render)
self.master.drawSurface('cubo', front, c=np.random.random(3), mode=self.render)
self.master.drawSurface('cubo', back, c=np.random.random(3), mode=self.render)
self.master.drawSurface('cubo', right, c=np.random.random(3), mode=self.render)
self.master.drawSurface('cubo', left, c=np.random.random(3), mode=self.render)
用线条勾勒出的球和六面体:

用颜色表现出的球和六面体:
 用“前面填充颜色后面显示线条”的方式表现出的球和六面体:
用“前面填充颜色后面显示线条”的方式表现出的球和六面体:

8 地球
有了画球的经验,画地球就轻车熟路了。唯一不同的是,球体表面每一个点的颜色,要对应到平面图上。
# 从等经纬地图上读取经纬度网格上的每一个格点的颜色
c = np.array(Image.open('res/shadedrelief.png'))/255
# 生成和等经纬地图分辨率一致的经纬度网格,计算经纬度网格上的每一个格点的空间坐标(x,y,z)
lats, lons = np.mgrid[np.pi/2:-np.pi/2:complex(0,c.shape[0]), 0:2*np.pi:complex(0,c.shape[1])]
x = np.cos(lats)*np.cos(lons)
y = np.cos(lats)*np.sin(lons)
z = np.sin(lats)
self.master.drawMesh('earth', x, y, z, c)
self.master.update()
9 三维重建
基于头部CT断层扫描图片,可以完成头部的三维重建。在这类,我使用了体数据绘制的方法。
# 读取109张头部CT的断层扫描图片
data = np.stack([np.array(Image.open('res/head%d.png'%i)) for i in range(109)], axis=0)
data = np.rollaxis(data, 2, start=0)[::-1] # 反转数组轴(2轴变0轴),然后0轴逆序
# 三维重建(本质上是体数据绘制)
self.master.drawVolume('volume', data/255.0, method='Q', smooth=False)
self.master.update()
三维重建后的效果如下图。因为断层扫描不够精细,也没有插值,层与层之间的缝隙比较明显。如果断层数据足够多,效果还可以更好一些。







