经典算法大全51例——4.三色旗

算法目录合集

地址

   算法目录合集

说明

  该地址指向所有由本人自己所经历的算法习题(也有可能仅仅是一个入门的案例或者是经典案例)，仅仅为我做过而且比较有意思的，也许还会有一些我自己想出来的，出于兴趣写在这里,具体格式我会在下面列明，总目录也会在这里出现，方便查阅以及自己进行复习回顾。

题目以及个人题解

  三色旗的问题最早由E.W.Dijkstra所提出，他所使用的用语为Dutch Nation Flag(Dijkstra为荷兰人)，而多数的作者则使用Three-Color Flag来称之。
  假设有一条绳子，上面有红、白、蓝三种颜色的旗子，起初绳子上的旗子颜色并没有顺序，您希望将之分类，并排列为蓝、白、红的顺序，要如何移动次数才会最少，注意您只能在绳子上进行这个动作，而且一次只能调换两个旗子。

  特别说明

  经过我对题目的分析以及自己尝试过的其他答案和自己所进行的其他变形，我有个拙见：那就是这个旗子原本在绳子上的位置应该是不发生改变的（假如绳子分为0、1、2、3、4、5、6、7，这八个位置，其中2、3、4有旗子，操作过之后，旗子应该所在位置还是2、3、4），如果不加这个限制，是很容易讨巧的，具体我会在后面进行说明。

原理分析

  首先，大家不要讨巧，不要讨巧，不要讨巧！！！否则三体星人会惩戒你的！！！哈哈哈，这题可千万不要把颜色给用1，2，3给代表，然后再来个sort，太low了

  不瞎扯了，下面我说一下正确（自诩）的思路：

  面对这个题，最直观的想法就是：“我先一个一个看，如果是蓝色，就扔到队伍前面去，如果是红色，就扔到队伍后面去，如果是白色，那就不理他。”没错，这就是核心思路，那么怎么实现呢，不利用多余的数组空间，怎么把他们的位置进行置换？这就需要指针了，一个指针指向队伍头，代表蓝色旗子将要被扔的位置，第二个指针指向队伍尾，代表红色旗子将要被扔的位置，第三个指针（序列指针）从队伍头一直往后，对每个旗子进行颜色判断。

  值得说明的是：数组是固定的，当要把元素插入到第一个位置，必将导致大规模的变动，所以需要一个方法，置换两个旗子，如果是蓝色，就与队伍头置换，红色则置换队伍尾；所以这便是我们的核心代码（虽然简单，但是用处很大）：

	temp = a;
	a = b;
	b = temp;

  $temp$是临时储存元素，用来交换$a$与$b$，而交换完了之后，把指针进行位移（如果换了头部，则头部指针后移一位，如果换了尾部，则头部指针前移一位），这里仅仅指对头尾指针的操作，因为对于序列指针是需要分情况进行讨论的。

  惯例，定义好变量：

        String temp;
        int bFlag = 0;
        int rFlag = nums.length - 1;
        int search = 0;

  注意

  这里之所以把$search$也定位$0$，是因为并不知道第一个元素是什么颜色，①如果不是蓝色，那么自然是需要操作一下的，这种属于正常情况②如果是蓝色，$search$却从$1$开始，那么造成的结果就是极大可能有一个蓝色是没法进入头部队列的，因为假如旗子为“蓝白白白蓝红”，那么$search$从1开始，遇到了三个白色都跳过了，遇到了4号位的蓝色，就会和0号位置的蓝色互换，导致$4$号位还是蓝色；而把$search$设置为$0$，就是确保$0$号位即使是蓝色，也不会被$search$所“拐卖”走。

  然后理一下逻辑：当$while(search<=rFlag)$的时候进行指针的移动，一直到$search>rFlag$了，说明已经遍历完整个数组了，就不需要继续进行了。然后就是对$nums[search]$进行条件判断，不同的情况来进行不同操作，于是框架有了：

while (search <= rFlag){
     
	switch (nums[search]){
     
		case "蓝":
			//如果是蓝的进行的操作
			break;
		case "白":
			//如果是白的进行的操作
			break;
		case "红":
			//如果是红的进行的操作
			break;
		default:
			break;
	}
}

• 对于蓝色的操作：

  蓝色为队伍头的位置，对于他的操作分为这么几个步骤：①$search$序列指针进行搜索，发现该位置为蓝色；②将$search$与$bFlag$两个位置的旗子互换（利用临时值$temp$，不再赘述）；③$bFlag$指针后移（为了保证下次置换的旗子为队列头部的第一个非红色旗子），$search$指针后移（继续判断下一个旗子）。

		case "蓝":
			temp = nums[search];
			nums[search] = nums[bFlag];
			nums[bFlag] = temp;
			bFlag++;
			search++;
			break;

• 对于白色的操作：

  因为白色是不需要进行位置交换的，所以也不用进行交换，直接后移序列指针就行，就可以保证中间为白色了。

		case "白":
			search++;
			break;

• 对于红色的操作：

  红色的操作相较于蓝色有些特殊，具体我会在步骤之后说一下，红色旗子的操作步骤为：①$search$序列指针进行搜索，发现该位置为红色；②将$search$与$rFlag$两个位置的旗子互换（利用临时值$temp$，不再赘述）；③$rFlag$指针前移（为了保证下次置换的旗子为队列尾部的最后一个非蓝色旗子）。

  注意

  认真的猿发现了，这里的第三步并没有像操作红色旗子一样，去位移$search$，原因其实和$search$赋值为$0$而不是$1$的原因大同小异：试想一下，我们只是对$search$进行了判断，那么是不是队伍尾部换过来的那个旗子的颜色我们并不知道？比如：“蓝红白白蓝红”，$search$指针开始判断$1$号位置，发现了是红色，那么与队伍尾部红色进行交换，好的那么队列变成了“蓝红白白蓝红”，这时候rFlag指针已经指向了$4$号位置（倒数第二个），此时如果$search+1$，是不是就把$1$号位的红色跳过去了？没错，又被$search$“绑架”了，所以此时$search$不能$+1$，依旧要对此元素进行判断。

		case "红":
			temp = nums[search];
			nums[search] = nums[rFlag];
			nums[rFlag] = temp;
			rFlag--;
			break;

  题外话：
  最终可以发现，$search$没有移动到队伍末尾，但是其实他已经遍历了整个数组了。

代码实现——Java

/**
 * com
 *
 * @author g55zhw
 * @create 2020-09-18-09-41
 */
public class SortFlag {
     
    public void sortColors(String[] nums) {
     
        //按照蓝色、白色、红色顺序排列
        String temp;
        int bFlag = 0;
        int rFlag = nums.length - 1;
        int search = 0;
        while (search <= rFlag){
     
            switch (nums[search]){
     
                case "蓝":
                    temp = nums[search];
                    nums[search] = nums[bFlag];
                    nums[bFlag] = temp;
                    bFlag++;
                    search++;
                    break;
                case "白":
                    search++;
                    break;
                case "红":
                    temp = nums[search];
                    nums[search] = nums[rFlag];
                    nums[rFlag] = temp;
                    rFlag--;
                    break;
                default:
                    break;
            }
        }
    }
}

测试代码

/**
 * com
 *
 * @author g55zhw
 * @create 2020-09-18-09-41
 */
public class SortFlagTest {
     

    @Test
    public void sortColors() {
     
        SortFlag s = new SortFlag();
        String[] arr = new String[]{
     "红","白","蓝","红","蓝","白","蓝","蓝","红","白"};
        s.sortColors(arr);
        System.out.println(Arrays.toString(arr));
    }
}

结果演示

[蓝, 蓝, 蓝, 蓝, 白, 白, 白, 红, 红, 红]

相关题目其他变形：

1.颜色分类（来源：力扣LeetCode）

  这个力扣的三色旗问题是非常基础的，在这里就不做过多的计算了，仅仅把旗子匹配颜色置换成数字就可以了，大家自己看看把，我的leetcode也不收录了，没啥意思，链接给你们，自己去看，可以练练手，75.颜色分类（不过那里面用其他方式的解题思路大家可以看看，学习学习，思路学会了真的很重要）。

2.五色旗

分析

  五色旗其实操作原理是一模一样，只不过刚开始先把需要排列再最中间的三种颜色进行过滤（当成三色旗里的白色一样，不去理会），等把两端的旗子排好之后，再操作中间的三种颜色，然后就可以实现了，多色就每次只整理两端的旗子，慢慢压缩到中间，即可。(四色原理一样,多色也可以此类推)

代码实现

package com;

/**
 * com
 *
 * @author g55zhw
 * @create 2020-09-18-14-52
 */
public class SortFlagFive {
     
    public void sortColors(String[] nums) {
     
        //按照红色、白色、蓝色、绿色、黑色顺序排列。
        String temp;
        int head = 0;
        int tail = nums.length - 1;
        int search = 0;
        while (search <= tail){
     
            switch (nums[search]){
     
                case "红":
                    temp = nums[search];
                    nums[search] = nums[head];
                    nums[head] = temp;
                    head++;
                    search++;
                    break;
                case "白":
                case "蓝":
                case "绿":
                    search++;
                    break;
                case "黑":
                    temp = nums[search];
                    nums[search] = nums[tail];
                    nums[tail] = temp;
                    tail--;
                    break;
                default:
                    break;
            }
        }
        search = head;
        while (search <= tail){
     
            switch (nums[search]){
     
                case "白":
                    temp = nums[search];
                    nums[search] = nums[head];
                    nums[head] = temp;
                    head++;
                    search++;
                    break;
                case "蓝":
                    search++;
                    break;
                case "绿":
                    temp = nums[search];
                    nums[search] = nums[tail];
                    nums[tail] = temp;
                    tail--;
                    break;
                default:
                    break;
            }
        }
    }
}

测试代码

/**
 * com
 *
 * @author g55zhw
 * @create 2020-09-18-14-55
 */
public class SortFlagTest {
     
    @Test
    public void sortColorsFive() {
     
        SortFlagFive s = new SortFlagFive();
        String[] arr = new String[]{
     "红","白","蓝","红","白","蓝","绿","黑","红","绿","黑","绿","黑","红","白","蓝","绿","黑","绿","黑","红"};
        s.sortColors(arr);
        System.out.println(Arrays.toString(arr));
    }
}

结果演示

[红, 红, 红, 红, 红, 白, 白, 白, 蓝, 蓝, 蓝, 绿, 绿, 绿, 绿, 绿, 黑, 黑, 黑, 黑, 黑]

官方题解

解法

  在一条绳子上移动，在程式中也就意味只能使用一个阵列，而不使用其它的阵列来作辅助，问题的解法很简单，您可以自己想像一下在移动旗子，从绳子开头进行，遇到蓝色往前移，遇到白色留在中间，遇到红色往后移，如下所示：
  只是要让移动次数最少的话，就要有些技巧：

• 如果图中W所在的位置为白色，则W+1，表示未处理的部份移至至白色群组。
• 如果W部份为蓝色，则B与W的元素对调，而B与W必须各+1，表示两个群组都多了一个元素。
• 如果W所在的位置是红色，则将W与R交换，但R要减1，表示未处理的部份减1。
  
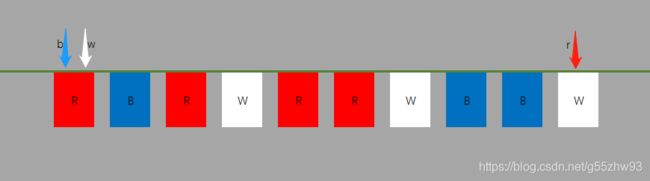
    注意B、W、R并不是三色旗的个数，它们只是一个移动的指标；什幺时候移动结束呢？一开始时未处理的R指标会是等于旗子的总数，当R的索引数减至少于W的索引数时，表示接下来的旗子就都是红色了，此时就可以结束移动。

代码——C语言

#include 
#include 
#include 
#define BLUE 'b'
#define WHITE 'w'
#define RED	'r'
#define SWAP( x, y ) { char temp; \
		       temp	= color[x]; \
		       color[x] = color[y]; \
		       color[y] = temp; }
int main(){
     
	char color[] = {
      'r', 'w', 'b', 'w', 'w', 'b', 'r', 'b', 'w', 'r','\0' };
	int	wFlag = 0;
	int	bFlag = 0;
	int	rFlag = strlen( color ) - 1;
	int	i;
	for ( i = 0; i < strlen( color ); i++ ){
     
		printf( "%c ", color[i] );
	}
	printf( "\n" );
	while ( wFlag <= rFlag ){
     
		if ( color[wFlag] == WHITE ){
     
			wFlag++;
		}
		else if ( color[wFlag] == BLUE ){
     
			SWAP( bFlag, wFlag );
			bFlag++; 
			wFlag++;
		}else {
     
			while ( wFlag < rFlag && color[rFlag] == RED ){
     
				rFlag--;
			}
			SWAP( rFlag, wFlag );
			rFlag--;
		}
	}
	for ( i = 0; i < strlen( color ); i++ ){
     
		printf( "%c ", color[i] );
	}
	printf( "\n" );
	return(0);
}