- c++ 的iostream 和 c++的stdio的区别和联系
黄卷青灯77
c++算法开发语言iostreamstdio
在C++中,iostream和C语言的stdio.h都是用于处理输入输出的库,但它们在设计、用法和功能上有许多不同。以下是两者的区别和联系:区别1.编程风格iostream(C++风格):C++标准库中的输入输出流类库,支持面向对象的输入输出操作。典型用法是cin(输入)和cout(输出),使用>操作符来处理数据。更加类型安全,支持用户自定义类型的输入输出。#includeintmain(){in
- 【JS】执行时长(100分) |思路参考+代码解析(C++)
l939035548
JS算法数据结构c++
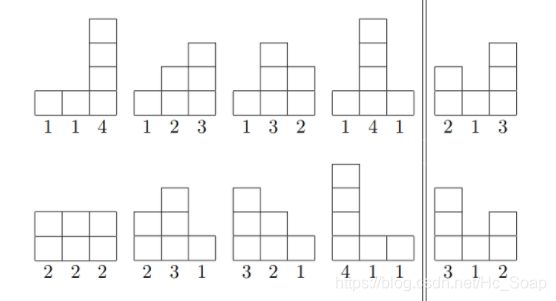
题目为了充分发挥GPU算力,需要尽可能多的将任务交给GPU执行,现在有一个任务数组,数组元素表示在这1秒内新增的任务个数且每秒都有新增任务。假设GPU最多一次执行n个任务,一次执行耗时1秒,在保证GPU不空闲情况下,最少需要多长时间执行完成。题目输入第一个参数为GPU一次最多执行的任务个数,取值范围[1,10000]第二个参数为任务数组长度,取值范围[1,10000]第三个参数为任务数组,数字范围
- 基于CODESYS的多轴运动控制程序框架:逻辑与运动控制分离,快速开发灵活操作
GPJnCrbBdl
python开发语言
基于codesys开发的多轴运动控制程序框架,将逻辑与运动控制分离,将单轴控制封装成功能块,对该功能块的操作包含了所有的单轴控制(归零、点动、相对定位、绝对定位、设置当前位置、伺服模式切换等等)。程序框架由主程序按照状态调用分归零模式、手动模式、自动模式、故障模式,程序状态的跳转都已完成,只需要根据不同的工艺要求完成所需的动作即可。变量的声明、地址的规划都严格按照C++的标准定义,能帮助开发者快速
- C++ | Leetcode C++题解之第409题最长回文串
Ddddddd_158
经验分享C++Leetcode题解
题目:题解:classSolution{public:intlongestPalindrome(strings){unordered_mapcount;intans=0;for(charc:s)++count[c];for(autop:count){intv=p.second;ans+=v/2*2;if(v%2==1andans%2==0)++ans;}returnans;}};
- C++菜鸟教程 - 从入门到精通 第二节
DreamByte
c++
一.上节课的补充(数据类型)1.前言继上节课,我们主要讲解了输入,输出和运算符,我们现在来补充一下数据类型的知识上节课遗漏了这个知识点,非常的抱歉顺便说一下,博主要上高中了,更新会慢,2-4周更新一次对了,正好赶上中秋节,小编跟大家说一句:中秋节快乐!2.int类型上节课,我们其实只用了int类型int类型,是整数类型,它们存贮的是整数,不能存小数(浮点数)定义变量的方式很简单inta;//定义一
- 网络编程基础
记得开心一点啊
网络
目录♫什么是网络编程♫Socket套接字♪什么是Socket套接字♪数据报套接字♪流套接字♫数据报套接字通信模型♪数据报套接字通讯模型♪DatagramSocket♪DatagramPacket♪实现UDP的服务端代码♪实现UDP的客户端代码♫流套接字通信模型♪流套接字通讯模型♪ServerSocket♪Socket♪实现TCP的服务端代码♪实现TCP的客户端代码♫什么是网络编程网络编程,指网络上
- Java面试题精选:消息队列(二)
芒果不是芒
Java面试题精选javakafka
一、Kafka的特性1.消息持久化:消息存储在磁盘,所以消息不会丢失2.高吞吐量:可以轻松实现单机百万级别的并发3.扩展性:扩展性强,还是动态扩展4.多客户端支持:支持多种语言(Java、C、C++、GO、)5.KafkaStreams(一个天生的流处理):在双十一或者销售大屏就会用到这种流处理。使用KafkaStreams可以快速的把销售额统计出来6.安全机制:Kafka进行生产或者消费的时候会
- (179)时序收敛--->(29)时序收敛二九
FPGA系统设计指南针
FPGA系统设计(内训)fpga开发时序收敛
1目录(a)FPGA简介(b)Verilog简介(c)时钟简介(d)时序收敛二九(e)结束1FPGA简介(a)FPGA(FieldProgrammableGateArray)是在PAL(可编程阵列逻辑)、GAL(通用阵列逻辑)等可编程器件的基础上进一步发展的产物。它是作为专用集成电路(ASIC)领域中的一种半定制电路而出现的,既解决了定制电路的不足,又克服了原有可编程器件门电路数有限的缺点。(b)
- (180)时序收敛--->(30)时序收敛三十
FPGA系统设计指南针
FPGA系统设计(内训)fpga开发时序收敛
1目录(a)FPGA简介(b)Verilog简介(c)时钟简介(d)时序收敛三十(e)结束1FPGA简介(a)FPGA(FieldProgrammableGateArray)是在PAL(可编程阵列逻辑)、GAL(通用阵列逻辑)等可编程器件的基础上进一步发展的产物。它是作为专用集成电路(ASIC)领域中的一种半定制电路而出现的,既解决了定制电路的不足,又克服了原有可编程器件门电路数有限的缺点。(b)
- (158)时序收敛--->(08)时序收敛八
FPGA系统设计指南针
FPGA系统设计(内训)fpga开发时序收敛
1目录(a)FPGA简介(b)Verilog简介(c)时钟简介(d)时序收敛八(e)结束1FPGA简介(a)FPGA(FieldProgrammableGateArray)是在PAL(可编程阵列逻辑)、GAL(通用阵列逻辑)等可编程器件的基础上进一步发展的产物。它是作为专用集成电路(ASIC)领域中的一种半定制电路而出现的,既解决了定制电路的不足,又克服了原有可编程器件门电路数有限的缺点。(b)F
- (159)时序收敛--->(09)时序收敛九
FPGA系统设计指南针
FPGA系统设计(内训)fpga开发时序收敛
1目录(a)FPGA简介(b)Verilog简介(c)时钟简介(d)时序收敛九(e)结束1FPGA简介(a)FPGA(FieldProgrammableGateArray)是在PAL(可编程阵列逻辑)、GAL(通用阵列逻辑)等可编程器件的基础上进一步发展的产物。它是作为专用集成电路(ASIC)领域中的一种半定制电路而出现的,既解决了定制电路的不足,又克服了原有可编程器件门电路数有限的缺点。(b)F
- (160)时序收敛--->(10)时序收敛十
FPGA系统设计指南针
FPGA系统设计(内训)fpga开发时序收敛
1目录(a)FPGA简介(b)Verilog简介(c)时钟简介(d)时序收敛十(e)结束1FPGA简介(a)FPGA(FieldProgrammableGateArray)是在PAL(可编程阵列逻辑)、GAL(通用阵列逻辑)等可编程器件的基础上进一步发展的产物。它是作为专用集成电路(ASIC)领域中的一种半定制电路而出现的,既解决了定制电路的不足,又克服了原有可编程器件门电路数有限的缺点。(b)F
- (153)时序收敛--->(03)时序收敛三
FPGA系统设计指南针
FPGA系统设计(内训)fpga开发时序收敛
1目录(a)FPGA简介(b)Verilog简介(c)时钟简介(d)时序收敛三(e)结束1FPGA简介(a)FPGA(FieldProgrammableGateArray)是在PAL(可编程阵列逻辑)、GAL(通用阵列逻辑)等可编程器件的基础上进一步发展的产物。它是作为专用集成电路(ASIC)领域中的一种半定制电路而出现的,既解决了定制电路的不足,又克服了原有可编程器件门电路数有限的缺点。(b)F
- (121)DAC接口--->(006)基于FPGA实现DAC8811接口
FPGA系统设计指南针
FPGA接口开发(项目实战)fpga开发FPGAIC
1目录(a)FPGA简介(b)IC简介(c)Verilog简介(d)基于FPGA实现DAC8811接口(e)结束1FPGA简介(a)FPGA(FieldProgrammableGateArray)是在PAL(可编程阵列逻辑)、GAL(通用阵列逻辑)等可编程器件的基础上进一步发展的产物。它是作为专用集成电路(ASIC)领域中的一种半定制电路而出现的,既解决了定制电路的不足,又克服了原有可编程器件门电
- FPGA复位专题---(3)上电复位?
FPGA系统设计指南针
FPGA系统设计(内训)fpga开发
(3)上电复位?1目录(a)FPGA简介(b)Verilog简介(c)复位简介(d)上电复位?(e)结束1FPGA简介(a)FPGA(FieldProgrammableGateArray)是在PAL(可编程阵列逻辑)、GAL(通用阵列逻辑)等可编程器件的基础上进一步发展的产物。它是作为专用集成电路(ASIC)领域中的一种半定制电路而出现的,既解决了定制电路的不足,又克服了原有可编程器件门电路数有限
- (182)时序收敛--->(32)时序收敛三二
FPGA系统设计指南针
FPGA系统设计(内训)fpga开发时序收敛
1目录(a)FPGA简介(b)Verilog简介(c)时钟简介(d)时序收敛三二(e)结束1FPGA简介(a)FPGA(FieldProgrammableGateArray)是在PAL(可编程阵列逻辑)、GAL(通用阵列逻辑)等可编程器件的基础上进一步发展的产物。它是作为专用集成电路(ASIC)领域中的一种半定制电路而出现的,既解决了定制电路的不足,又克服了原有可编程器件门电路数有限的缺点。(b)
- C++ lambda闭包消除类成员变量
barbyQAQ
c++c++java算法
原文链接:https://blog.csdn.net/qq_51470638/article/details/142151502一、背景在面向对象编程时,常常要添加类成员变量。然而类成员一旦多了之后,也会带来干扰。拿到一个类,一看成员变量好几十个,就问你怕不怕?二、解决思路可以借助函数式编程思想,来消除一些不必要的类成员变量。三、实例举个例子:classClassA{public:...intfu
- 2021 CCF 非专业级别软件能力认证第一轮(CSP-J1)入门级C++语言试题 (第三大题:完善程序 代码)
mmz1207
c++csp
最近有一段时间没更新了,在准备CSP考试,请大家见谅。(1)有n个人围成一个圈,依次标号0到n-1。从0号开始,依次0,1,0,1...交替报数,报到一的人离开,直至圈中剩最后一个人。求最后剩下的人的编号。#includeusingnamespacestd;intf[1000010];intmain(){intn;cin>>n;inti=0,cnt=0,p=0;while(cnt#includeu
- 《 C++ 修炼全景指南:九 》打破编程瓶颈!掌握二叉搜索树的高效实现与技巧
Lenyiin
C++修炼全景指南技术指南c++算法stl
摘要本文详细探讨了二叉搜索树(BinarySearchTree,BST)的核心概念和技术细节,包括插入、查找、删除、遍历等基本操作,并结合实际代码演示了如何实现这些功能。文章深入分析了二叉搜索树的性能优势及其时间复杂度,同时介绍了前驱、后继的查找方法等高级功能。通过自定义实现的二叉搜索树类,读者能够掌握其实际应用,此外,文章还建议进一步扩展为平衡树(如AVL树、红黑树)以优化极端情况下的性能退化。
- 20个新手学习c++必会的程序 输出*三角形、杨辉三角等(附代码)
X_StarX
c++学习算法大学生开发语言数据结构
示例1:HelloWorld#includeusingnamespacestd;intmain(){coutusingnamespacestd;intmain(){inta=5;intb=10;intsum=a+b;coutusingnamespacestd;intfactorial(intn){if(nusingnamespacestd;voidprintFibonacci(intn){intt
- C++八股
Petrichorzncu
八股总结c++开发语言
这里写目录标题C++内存管理C++的构造函数,复制构造函数,和析构函数深复制与浅复制:构造函数和析构函数哪个能写成虚函数,为什么?C++数据结构内存排列结构体和类占用的内存:==虚函数和虚表的原理==虚函数虚表(Vtable)虚函数和虚表的实现细节==内存泄漏==指针的工作原理函数的传值和传址new和delete与malloc和freeC++内存区域划分C++11新特性C++常见新特性==智能指针
- 【2022 CCF 非专业级别软件能力认证第一轮(CSP-J1)入门级 C++语言试题及解析】
汉子萌萌哒
CCFnoi算法数据结构c++
一、单项选择题(共15题,每题2分,共计30分;每题有且仅有一个正确选项)1.以下哪种功能没有涉及C++语言的面向对象特性支持:()。A.C++中调用printf函数B.C++中调用用户定义的类成员函数C.C++中构造一个class或structD.C++中构造来源于同一基类的多个派生类题目解析【解析】正确答案:AC++基础知识,面向对象和类有关,类又涉及父类、子类、继承、派生等关系,printf
- 《 C++ 修炼全景指南:十 》自平衡的艺术:深入了解 AVL 树的核心原理与实现
Lenyiin
C++修炼全景指南技术指南c++数据结构stl
摘要本文深入探讨了AVL树(自平衡二叉搜索树)的概念、特点以及实现细节。我们首先介绍了AVL树的基本原理,并详细分析了其四种旋转操作,包括左旋、右旋、左右双旋和右左双旋,阐述了它们在保持树平衡中的重要作用。接着,本文从头到尾详细描述了AVL树的插入、删除和查找操作,配合完整的代码实现和详尽的注释,使读者能够全面理解这些操作的执行过程。此外,我们还提供了AVL树的遍历方法,包括中序、前序和后序遍历,
- 计算机网络八股总结
Petrichorzncu
八股总结计算机网络笔记
这里写目录标题网络模型划分(五层和七层)及每一层的功能五层网络模型七层网络模型(OSI模型)==三次握手和四次挥手具体过程及原因==三次握手四次挥手TCP/IP协议组成==UDP协议与TCP/IP协议的区别==Http协议相关知识网络地址,子网掩码等相关计算网络模型划分(五层和七层)及每一层的功能五层网络模型应用层:负责处理网络应用程序,如电子邮件、文件传输和网页浏览。主要协议包括HTTP、FTP
- ubuntu安装wordpress
lissettecarlr
1安装nginx网上安装方式很多,这就就直接用apt-get了apt-getinstallnginx不用启动啥,然后直接在浏览器里面输入IP:80就能看到nginx的主页了。如果修改了一些配置可以使用下列命令重启一下systemctlrestartnginx.service2安装mysql输入安装前也可以更新一下软件源,在安装过程中将会让你输入数据库的密码。sudoapt-getinstallmy
- JAVA学习笔记之23种设计模式学习
victorfreedom
Java技术设计模式androidjava常用设计模式
博主最近买了《设计模式》这本书来学习,无奈这本书是以C++语言为基础进行说明,整个学习流程下来效率不是很高,虽然有的设计模式通俗易懂,但感觉还是没有充分的掌握了所有的设计模式。于是博主百度了一番,发现有大神写过了这方面的问题,于是博主迅速拿来学习。一、设计模式的分类总体来说设计模式分为三大类:创建型模式,共五种:工厂方法模式、抽象工厂模式、单例模式、建造者模式、原型模式。结构型模式,共七种:适配器
- 解决Obsidian写笔记中的<img>标签无法显示图片的问题
全能全知者
笔记
Obsidian中写md笔记如果使用标签会显示不出图案,后来才知道因为Obsidian的问题导致只能用绝对路径定位。所以我本人写了一个py插件,将md笔记里的img标签批量替换成Obsidian能够读取的形式。安装FixObsImgDpy:pipinstallFixObsImgDpy安装完成后在需要修复的md文件的父目录下运行命令:FixObsImgDpy就会自动修复父目录以下的全部md文件 仓库
- c++ opencv4.3 sift匹配
图像处理大大大大大牛啊
图像处理opencv实战代码讲解opencvsiftc++opencv4特征点
c++opencv4.3sift匹配main.cppintmain(){vectorkeypoints1,keypoints2;Matimg1,img2,descriptors1,descriptors2;intnumF
- 《 C++ 修炼全景指南:四 》揭秘 C++ List 容器背后的实现原理,带你构建自己的双向链表
Lenyiin
技术指南C++修炼全景指南c++list链表stl
本篇博客,我们将详细讲解如何从头实现一个功能齐全且强大的C++List容器,并深入到各个细节。这篇博客将包括每一步的代码实现、解释以及扩展功能的探讨,目标是让初学者也能轻松理解。一、简介1.1、背景介绍在C++中,std::list是一个基于双向链表的容器,允许高效的插入和删除操作,适用于频繁插入和删除操作的场景。与动态数组不同,list允许常数时间内的插入和删除操作,支持双向遍历。这篇文章将详细
- c++ 内存处理函数
heeheeai
c++开发语言
在C语言的头文件中,memcpy和memmove函数都用于复制内存块,但它们在处理内存重叠方面存在关键区别:内存重叠:memcpy函数不保证在源内存和目标内存区域重叠时能够正确复制数据。如果内存区域重叠,memcpy的行为是未定义的,可能会导致数据损坏或程序崩溃。memmove函数能够安全地处理源内存和目标内存区域重叠的情况。它会确保在复制过程中不会覆盖尚未复制的数据,从而保证数据的完整性。效率:
- C/C++Win32编程基础详解视频下载
择善Zach
编程C++Win32
课题视频:C/C++Win32编程基础详解
视频知识:win32窗口的创建
windows事件机制
主讲:择善Uncle老师
学习交流群:386620625
验证码:625
--
- Guava Cache使用笔记
bylijinnan
javaguavacache
1.Guava Cache的get/getIfPresent方法当参数为null时会抛空指针异常
我刚开始使用时还以为Guava Cache跟HashMap一样,get(null)返回null。
实际上Guava整体设计思想就是拒绝null的,很多地方都会执行com.google.common.base.Preconditions.checkNotNull的检查。
2.Guava
- 解决ora-01652无法通过128(在temp表空间中)
0624chenhong
oracle
解决ora-01652无法通过128(在temp表空间中)扩展temp段的过程
一个sql语句后,大约花了10分钟,好不容易有一个结果,但是报了一个ora-01652错误,查阅了oracle的错误代码说明:意思是指temp表空间无法自动扩展temp段。这种问题一般有两种原因:一是临时表空间空间太小,二是不能自动扩展。
分析过程:
既然是temp表空间有问题,那当
- Struct在jsp标签
不懂事的小屁孩
struct
非UI标签介绍:
控制类标签:
1:程序流程控制标签 if elseif else
<s:if test="isUsed">
<span class="label label-success">True</span>
</
- 按对象属性排序
换个号韩国红果果
JavaScript对象排序
利用JavaScript进行对象排序,根据用户的年龄排序展示
<script>
var bob={
name;bob,
age:30
}
var peter={
name;peter,
age:30
}
var amy={
name;amy,
age:24
}
var mike={
name;mike,
age:29
}
var john={
- 大数据分析让个性化的客户体验不再遥远
蓝儿唯美
数据分析
顾客通过多种渠道制造大量数据,企业则热衷于利用这些信息来实现更为个性化的体验。
分析公司Gartner表示,高级分析会成为客户服务的关键,但是大数据分析的采用目前仅局限于不到一成的企业。 挑战在于企业还在努力适应结构化数据,疲于根据自身的客户关系管理(CRM)系统部署有效的分析框架,以及集成不同的内外部信息源。
然而,面对顾客通过数字技术参与而产生的快速变化的信息,企业需要及时作出反应。要想实
- java笔记4
a-john
java
操作符
1,使用java操作符
操作符接受一个或多个参数,并生成一个新值。参数的形式与普通的方法调用不用,但是效果是相同的。加号和一元的正号(+)、减号和一元的负号(-)、乘号(*)、除号(/)以及赋值号(=)的用法与其他编程语言类似。
操作符作用于操作数,生成一个新值。另外,有些操作符可能会改变操作数自身的
- 从裸机编程到嵌入式Linux编程思想的转变------分而治之:驱动和应用程序
aijuans
嵌入式学习
笔者学习嵌入式Linux也有一段时间了,很奇怪的是很多书讲驱动编程方面的知识,也有很多书将ARM9方面的知识,但是从以前51形式的(对寄存器直接操作,初始化芯片的功能模块)编程方法,和思维模式,变换为基于Linux操作系统编程,讲这个思想转变的书几乎没有,让初学者走了很多弯路,撞了很多难墙。
笔者因此写上自己的学习心得,希望能给和我一样转变
- 在springmvc中解决FastJson循环引用的问题
asialee
循环引用fastjson
我们先来看一个例子:
package com.elong.bms;
import java.io.OutputStream;
import java.util.HashMap;
import java.util.Map;
import co
- ArrayAdapter和SimpleAdapter技术总结
百合不是茶
androidSimpleAdapterArrayAdapter高级组件基础
ArrayAdapter比较简单,但它只能用于显示文字。而SimpleAdapter则有很强的扩展性,可以自定义出各种效果
ArrayAdapter;的数据可以是数组或者是队列
// 获得下拉框对象
AutoCompleteTextView textview = (AutoCompleteTextView) this
- 九封信
bijian1013
人生励志
有时候,莫名的心情不好,不想和任何人说话,只想一个人静静的发呆。有时候,想一个人躲起来脆弱,不愿别人看到自己的伤口。有时候,走过熟悉的街角,看到熟悉的背影,突然想起一个人的脸。有时候,发现自己一夜之间就长大了。 2014,写给人
- Linux下安装MySQL Web 管理工具phpMyAdmin
sunjing
PHPInstallphpMyAdmin
PHP http://php.net/
phpMyAdmin http://www.phpmyadmin.net
Error compiling PHP on CentOS x64
一、安装Apache
请参阅http://billben.iteye.com/admin/blogs/1985244
二、安装依赖包
sudo yum install gd
- 分布式系统理论
bit1129
分布式
FLP
One famous theory in distributed computing, known as FLP after the authors Fischer, Lynch, and Patterson, proved that in a distributed system with asynchronous communication and process crashes,
- ssh2整合(spring+struts2+hibernate)-附源码
白糖_
eclipsespringHibernatemysql项目管理
最近抽空又整理了一套ssh2框架,主要使用的技术如下:
spring做容器,管理了三层(dao,service,actioin)的对象
struts2实现与页面交互(MVC),自己做了一个异常拦截器,能拦截Action层抛出的异常
hibernate与数据库交互
BoneCp数据库连接池,据说比其它数据库连接池快20倍,仅仅是据说
MySql数据库
项目用eclipse
- treetable bug记录
braveCS
table
// 插入子节点删除再插入时不能正常显示。修改:
//不知改后有没有错,先做个备忘
Tree.prototype.removeNode = function(node) {
// Recursively remove all descendants of +node+
this.unloadBranch(node);
// Remove
- 编程之美-电话号码对应英语单词
bylijinnan
java算法编程之美
import java.util.Arrays;
public class NumberToWord {
/**
* 编程之美 电话号码对应英语单词
* 题目:
* 手机上的拨号盘,每个数字都对应一些字母,比如2对应ABC,3对应DEF.........,8对应TUV,9对应WXYZ,
* 要求对一段数字,输出其代表的所有可能的字母组合
- jquery ajax读书笔记
chengxuyuancsdn
jQuery ajax
1、jsp页面
<%@ page language="java" import="java.util.*" pageEncoding="GBK"%>
<%
String path = request.getContextPath();
String basePath = request.getScheme()
- JWFD工作流拓扑结构解析伪码描述算法
comsci
数据结构算法工作活动J#
对工作流拓扑结构解析感兴趣的朋友可以下载附件,或者下载JWFD的全部代码进行分析
/* 流程图拓扑结构解析伪码描述算法
public java.util.ArrayList DFS(String graphid, String stepid, int j)
- oracle I/O 从属进程
daizj
oracle
I/O 从属进程
I/O从属进程用于为不支持异步I/O的系统或设备模拟异步I/O.例如,磁带设备(相当慢)就不支持异步I/O.通过使用I/O 从属进程,可以让磁带机模仿通常只为磁盘驱动器提供的功能。就好像支持真正的异步I/O 一样,写设备的进程(调用者)会收集大量数据,并交由写入器写出。数据成功地写出时,写入器(此时写入器是I/O 从属进程,而不是操作系统)会通知原来的调用者,调用者则会
- 高级排序:希尔排序
dieslrae
希尔排序
public void shellSort(int[] array){
int limit = 1;
int temp;
int index;
while(limit <= array.length/3){
limit = limit * 3 + 1;
- 初二下学期难记忆单词
dcj3sjt126com
englishword
kitchen 厨房
cupboard 厨柜
salt 盐
sugar 糖
oil 油
fork 叉;餐叉
spoon 匙;调羹
chopsticks 筷子
cabbage 卷心菜;洋白菜
soup 汤
Italian 意大利的
Indian 印度的
workplace 工作场所
even 甚至;更
Italy 意大利
laugh 笑
m
- Go语言使用MySQL数据库进行增删改查
dcj3sjt126com
mysql
目前Internet上流行的网站构架方式是LAMP,其中的M即MySQL, 作为数据库,MySQL以免费、开源、使用方便为优势成为了很多Web开发的后端数据库存储引擎。MySQL驱动Go中支持MySQL的驱动目前比较多,有如下几种,有些是支持database/sql标准,而有些是采用了自己的实现接口,常用的有如下几种:
http://code.google.c...o-mysql-dri
- git命令
shuizhaosi888
git
---------------设置全局用户名:
git config --global user.name "HanShuliang" //设置用户名
git config --global user.email "
[email protected]" //设置邮箱
---------------查看环境配置
git config --li
- qemu-kvm 网络 nat模式 (四)
haoningabc
kvmqemu
qemu-ifup-NAT
#!/bin/bash
BRIDGE=virbr0
NETWORK=192.168.122.0
GATEWAY=192.168.122.1
NETMASK=255.255.255.0
DHCPRANGE=192.168.122.2,192.168.122.254
TFTPROOT=
BOOTP=
function check_bridge()
- 不要让未来的你,讨厌现在的自己
jingjing0907
生活 奋斗 工作 梦想
故事one
23岁,他大学毕业,放弃了父母安排的稳定工作,独闯京城,在家小公司混个小职位,工作还算顺手,月薪三千,混了混,混走了一年的光阴。 24岁,有了女朋友,从二环12人的集体宿舍搬到香山民居,一间平房,二人世界,爱爱爱。偶然约三朋四友,打扑克搓麻将,日子快乐似神仙; 25岁,出了几次差,调了两次岗,薪水涨了不过百,生猛狂飙的物价让现实血淋淋,无力为心爱银儿购件大牌
- 枚举类型详解
一路欢笑一路走
enum枚举详解enumsetenumMap
枚举类型详解
一.Enum详解
1.1枚举类型的介绍
JDK1.5加入了一个全新的类型的”类”—枚举类型,为此JDK1.5引入了一个新的关键字enum,我们可以这样定义一个枚举类型。
Demo:一个最简单的枚举类
public enum ColorType {
RED
- 第11章 动画效果(上)
onestopweb
动画
index.html
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/
- Eclipse中jsp、js文件编辑时,卡死现象解决汇总
ljf_home
eclipsejsp卡死js卡死
使用Eclipse编辑jsp、js文件时,经常出现卡死现象,在网上百度了N次,经过N次优化调整后,卡死现象逐步好转,具体那个方法起到作用,不太好讲。将所有用过的方法罗列如下:
1、取消验证
windows–>perferences–>validation
把 除了manual 下面的全部点掉,build下只留 classpath dependency Valida
- MySQL编程中的6个重要的实用技巧
tomcat_oracle
mysql
每一行命令都是用分号(;)作为结束
对于MySQL,第一件你必须牢记的是它的每一行命令都是用分号(;)作为结束的,但当一行MySQL被插入在PHP代码中时,最好把后面的分号省略掉,例如:
mysql_query("INSERT INTO tablename(first_name,last_name)VALUES('$first_name',$last_name')");
- zoj 3820 Building Fire Stations(二分+bfs)
阿尔萨斯
Build
题目链接:zoj 3820 Building Fire Stations
题目大意:给定一棵树,选取两个建立加油站,问说所有点距离加油站距离的最大值的最小值是多少,并且任意输出一种建立加油站的方式。
解题思路:二分距离判断,判断函数的复杂度是o(n),这样的复杂度应该是o(nlogn),即使常数系数偏大,但是居然跑了4.5s,也是醉了。 判断函数里面做了3次bfs,但是每次bfs节点最多