高效生成所有的组合

这篇文章翻译自coolest way to generate combination,但不是全译，如有错误欢迎指出。

文章中把他们这个快速生成所有的组合的方法称为 cool-lex方法，特点是最后可以优化成没有循环和分支判断语句的执行代码。下面，我们先来介绍一些定义。

什么是前缀，什么是后缀我就不罗嗦了。定义\(S =s_1 ,s_2,s_3,\cdots s_m\)是一个字符串序列,字母集合为0，1。\(Sb = s_1 b,s_2 b,s_3 b,\cdots s_m b\) , \( S[i]=s_i\),\(first(S)=s_1\),\(last(S)=s_m\),\( \vec(S)=s_2,s_3,\cdots ,s_m,s_1\)。如果b是一个由0，1组成的字符串，且长度为n，则我们用\(l(b)\)表示为b中满足以010或011结尾的最短前缀的长度，如果不存在这个前缀，则\(l(b)\)是n。用\(p(b)\)表示这个最短前缀，然后用\(s(b)\)作为剩下的那一部分，则\(b=p(b)s(b)\)。让\(\sigma (b)\)作为将\(p(b)\)循环右移一位，然后再将\(s(b)\)附在其末尾的新字符串，并递归定义\(\sigma ^i (b)=\sigma (\sigma ^{i-1}(b))\),\(\sigma ^0 (b) = b\)。

然后，我们来分析在\(\sigma\)变换下，字符串的性质。在变换的过程中，\(1^t 0^s \)和\(1^{t-1} 0^s 1\)是非常重要的字符串，因为这些字符串是所有长度为\(s+t\)且刚好有\(t\)个1的字符串中仅有的满足不存在010和011子字符串的字符串。在变换下，我们有如下性质。

$$\sigma (b) 0 =\sigma (b0) \text{当且仅当} b\neq 1^{t-1}0^s1$$

$$\sigma (b) 1 = \sigma (b1) \text{ 当且仅当} b\neq 1^t 0^s with s \geq 1$$

$$ \sigma (1^{t-1}0^s1)=1^t 0^s$$

$$ \sigma (b) =\sigma (p(b))s(b)$$

我们有如下引理

\(\sigma (b)\) 只需要对b操作两次或一次字符交换来得到

证明如下：如果\(p(b)\)并不是以010或011结尾的，则\(b=1^t 0^s\)而且\(\sigma (b) = 01^t0^{s-1}\),或者\(b= 1^{t-1}0^s1\),此时\(\sigma (b)=1^t0^s\).在这两个情况下，\(\sigma (b)\)都可以通过交换b中两个字符的位置来得到。如果\(p(b)\)是以010或011结尾，那\(p(b)\)一定是一下几种形式的一种：\(00^i10,11^i00^j10,001^i1,11^i00^j11\)。对于这四种情况我们都可以通过最多交换两次来得到循环右移的值，对于相交换的两个位置，我们分别用下横线和上横线标出来。

$$\sigma (00^i10)=00^i\underline{10}=00^i01$$

$$\sigma (1^i00^j10)=\underline{1}1^i\underline{0}0^j\overline{10}=01^i10^j\overline{10}=011^i00^j1$$

$$\sigma (00^i11)=\underline{0}0^i\underline{1}1=100^i1$$

$$\sigma (11^i 00^j11)=11^i\underline{0}0^j\underline{1}1=111^i00^j1$$

现在我们定义一个\(R_{s,t}=\sigma ^0(b),\sigma ^1 (b),\cdots ,\sigma ^z (b)\),其中b为\(1^t0^s\),\(z=\binom {s+t} t -1\)。当\(s=1\) 或者\(t=1\)时，我们可以显示的给出\(R_{s,t}\)。

$$R_{1,t}=1^t0,01^t,101^{t-1},1^201^{t-2},\cdots ,1^{t-1}01$$

$$R_{s,1}=10^s,010^{s-1},0^210^{s-2},\cdots,0^s1$$

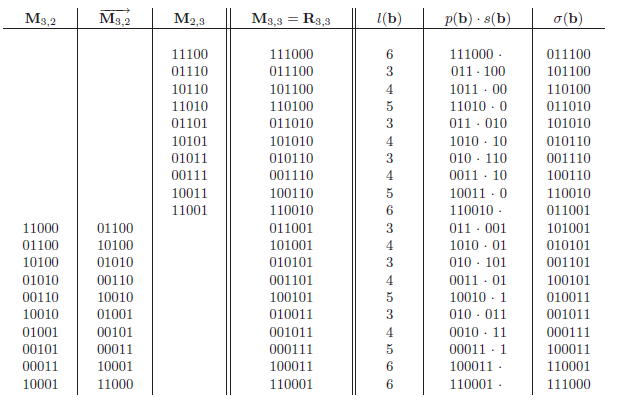
由上图我们可以看出\(R_{s,t}=R_{s-1,t}0,R_{s.t-1}1\),现在我们来数学归纳法证明\(R_{s,t}\)所生成的序列的确含有\(\binom {s+t} t\)个不同的序列，即完全生成了所有的组合。

当\(s=1\)或\(t=1\)时，我们可以手工判断这些成立，即刚好生成了所有的组合。

假设\(s\leq n\)和\(t\leq n\)时，上述结论都成立。现在来证明\(s\leq n+1\)和\(t\leq n+1\)时也成立。由\(R_{s,t}=R_{s-1,t}0,R_{s.t-1}1\)可知，当\(R_{s-1,t}\)和\(R_{s,t-1}\)都生成了相应的\(\binom {s+t-1} t\)和\(\binom {s+t-1} {t-1}\)个不同的组合时，\(R_{s,t}\)序列中的字符串都是不同的。又由于\(\binom {s+t-1} t+ \binom {s+t-1} {t-1} =\binom {s+t} t\)，所以\(R_{s,t}\)的确有\(\binom {s+t} t\)个不同的字符串，而且这些字符串中每一个都刚好只有t个1。

因此，上面证明了我们可以通过循环移位的方法得到所有的组合，但是根据循环移位的方法，我们每次都需要去寻找以011和010结尾的字符串，每次操作都需要\(O(s+t)\)次操作，时间消耗很大。我们在下面则采取一个简便的方法，通过两次交换，就可以得到下一个字符串，而不需要去寻找可行前缀并循环移位。在这里，我们先证明一个引理。

如果\(p(b)\)的确是以010或011结尾的，则\(\sigma (b)\) 可以通过从b中先交换位置\((x,y)\),然后再交换\((0,x+1)\)来得到。

证明： 如果\(p(b)\)的确是以010或011结尾的，则那\(p(b)\)一定是一下几种形式的一种：\(00^i10,11^i00^j10,001^i1,11^i00^j11\)。其实这里的证明也就是上一个引理的证明，这里我们把第一次交换的位置用下划线表示，第二次交换的位置有上划线表示。

$$\sigma (00^i10)=\underline{\overline {0}}0^i\underline{1}\overline{0}=\overline{1}0^i0\overline{0}=00^i01$$

$$\sigma (11^i00^j10)=\overline{1}1^i\underline{0}0^j\underline{1}\overline{0}=\overline{1}1^i10^j0\overline{0}=011^i00^j1$$

$$\sigma (00^i11)=\overline{\underline{0}}0^i\underline{1}\overline{1}=\overline{1}0^i0\overline{1}=100^i1$$

$$\sigma (11^i00^j11)=\overline{1}1^i\underline{0}0^j\underline{1}\overline{1}=\overline{1}1^i10^j0\overline{1}=111^i00^j1$$

由此我们可以得出以下结论：在得到正确的x，y的值的情况下，我们总是可以先交换（x，y）然后再交换(0,x+1)来得到\(\sigma\)变换下的新的字符串。对于(x,y),我们可以得出以下结论，一般情况下y都是加1，除非字符串的第一位在变换下被设置为0，此时y是0.同样，x在一般情况下也是加一，除非前两位被设置为01，此时x为2.

现在来说一下x，y代表的意义,x代表的是第一个使得b[x-1]=0&&b[x]=1的位置，y是第一个使得b[y]=0的位置。但是初始的时候我们找不到这个x，所以我们把x和y开始的时候都初始化为t-1。然后按照上述方案不停的交换位置，直到x到了末尾。

代码如下。

 1 #include <stdio.h>

 2 #include <malloc.h>

 3 #define NUMBER_ONE 3

 4 #define NUMBER_ZERO 2

 5 #define NUMBER_TOTAL (NUMBER_ZERO+NUMBER_ONE)

 6 int for_out[NUMBER_TOTAL];

 7 void result_out()

 8 {

 9     int for_i;

10     for(for_i=0;for_i<NUMBER_TOTAL;for_i++)

11     {

12         printf("%d ",*(for_out+for_i));

13     }

14     printf("\n");

15 }

16 void main()

17 {

18     int for_i,for_x,for_y;

19     for(for_i=0;for_i<NUMBER_ONE;for_i++)

20     {

21         *(for_out+for_i)=1;

22     }

23     for(for_i;for_i<NUMBER_TOTAL;for_i++)

24     {

25         *(for_out+for_i)=0;

26     }

27     result_out();

28     for_x=for_y=NUMBER_ONE-1;

29     while(for_x<(NUMBER_TOTAL-1))

30     {

31         for_out[for_x]=0;

32         for_out[for_y]=1;

33         for_out[0]=for_out[for_x+1];

34         for_out[for_x+1]=1;

35         for_x=1+(for_x)*(1-(for_out[1])*(1-for_out[0]));

36         for_y=for_out[0]*(for_y+1);

37         result_out();

38     }

39 }