【数据结构Python描述】优先级队列描述“银行VIP客户插队办理业务”及“被插队客户愤而离去”的模型实现

【数据结构Python描述】优先级队列简介及Python手工实现给出了优先级队列ADT的典型方法，这些方法对于如排序等常见应用已经足够，但在如下述的一些场景中，仍需要对优先级队列的ADT所包含的方法进行扩充：

• 一位土豪正在某银行排队办理业务，在等待过程中土豪突然发现自己是该行的VIP，在告知工作人员后，该土豪的排队优先级被提至最高；
• 本来排在土豪前面准备存钱的普通客户见状便找工作人员理论，后者告知前者土豪是VIP，根据该行规定有权享受这样的待遇，普通客户见沟通无果便要求删除自己取的号，然后愤而离去将存款存到了隔壁银行。

如果你想要直接体验实现上述情景的代码，请直接跳至第四部分。

一、支持插队模型的优先级队列

队列ADT扩充

分别对应上述两种情况，还需要在一般优先级队列ADT的基础上对其进行扩充，以增加下列两个方法：

• update(item, key, value)：将item中的key和value实例属性进行更新替换；
• remove(item)：从优先级队列中删除item并返回(key, value)。

队列记录描述

需要注意的是，由于update()和remove()方法的执行都有赖于先在优先级队列中找到对应的item，为了避免需要遍历存储所有item的列表，这里需要对item实例所属的类_Item进行升级，即为在其键值对(key, value)的基础上增添该条记录在列表中的索引idx，即一个item对象具有三个实例属性(key, value, idx)。

方法理论步骤

为了使得后续给出的上述两个新增方法的实现更容易理解，下面通过具体案例先从理论上分析每一个方法操作的步骤。

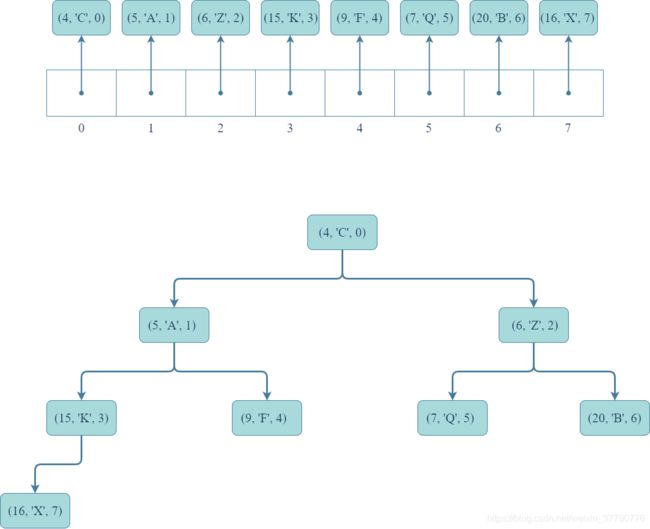
首先，假设分别通过以下两种形式给出一个已有的优先级队列的所有记录集合：

update(item, key, value)

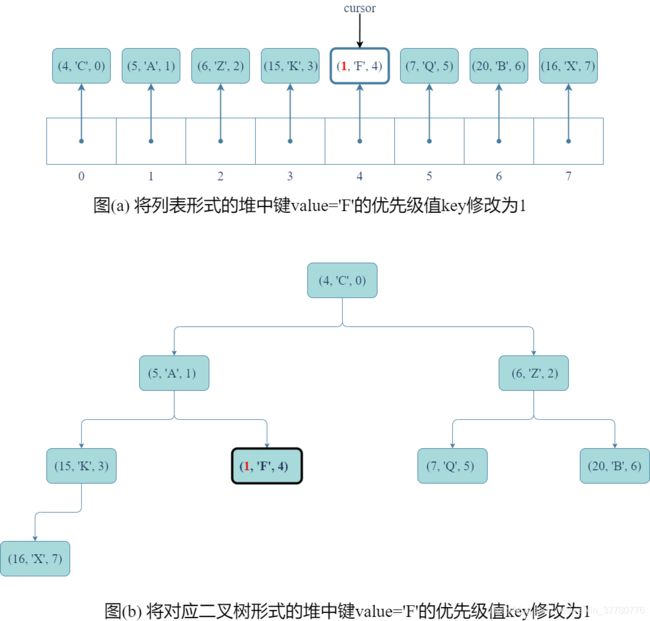
如果cursor = Item(9, 'F', 4)，则执行q.update(cursor, 1, 'F')的具体步骤如下：

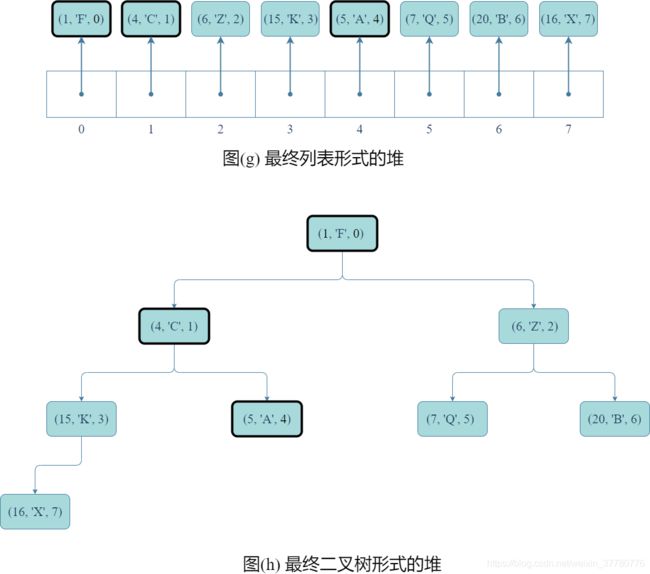
• 首先，如图(a)和(b)所示，将cursor所引用记录(9, 'F', 4)中的键修改为1（也可以此时同时修改值'F'为任意对象）。

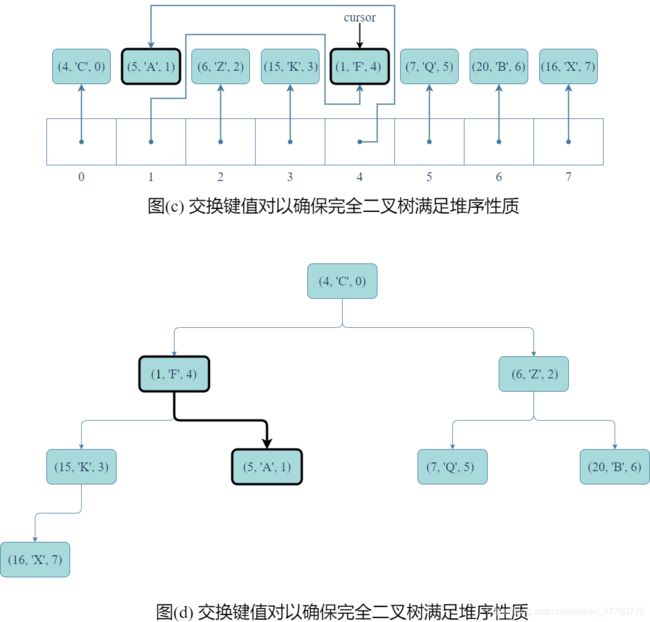
• 其次，如图(c)和(d)所示，为确保优先级队列某记录的键值修改后，底层的完全二叉树仍然是一个堆，需要进行结点间记录的交换；

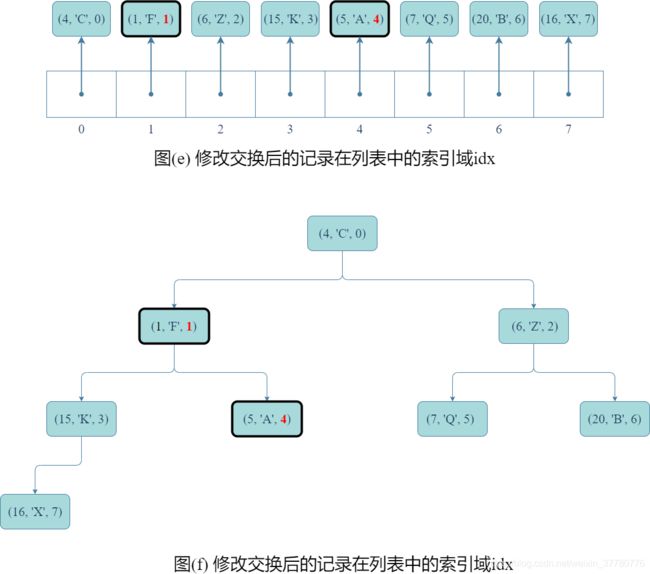
• 然后，如图(e)和(f)所示，为了使得交换后的记录的idx域都如实反应该条记录在列表中的索引，需要分别修改两条记录的idx；

• 接着，重复图©、(d)、(e)、(f)的步骤直到完全二叉树满足堆序性质且每条(key, value, idx)记录的idx域均如实反应该条记录在列表的位置。

remove(item)

下面还是以本节一开始的案例分析该方法操作的理论步骤，即如果item= Item(9, 'F', 4)，则执行q.remove(item)的具体步骤如下：

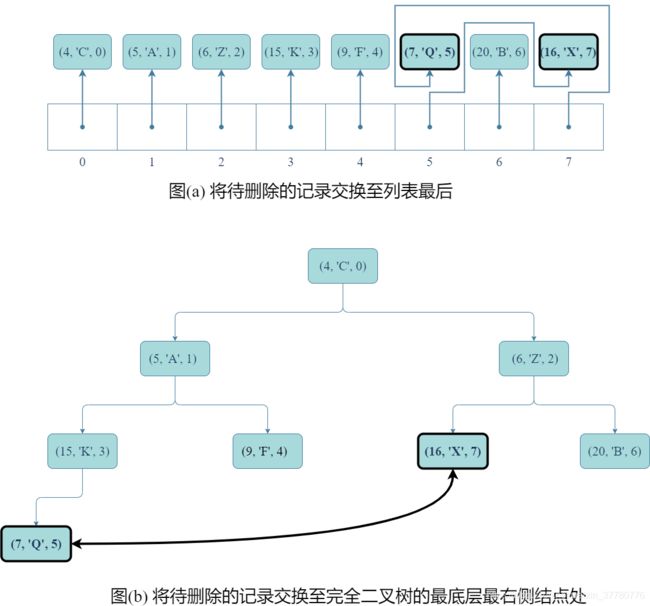
• 首先，如图(a)和(b)所示，将要删除的记录交换至列表尾部（即完全二叉树最底层最右侧结点处）；

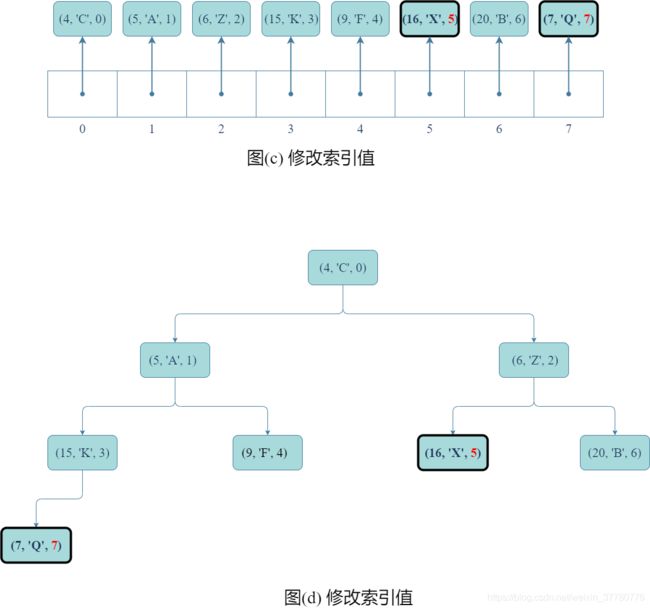
• 其次，如图©和(d)所示，类似上述分析update()方法，交换记录后需要修改记录的idx域；

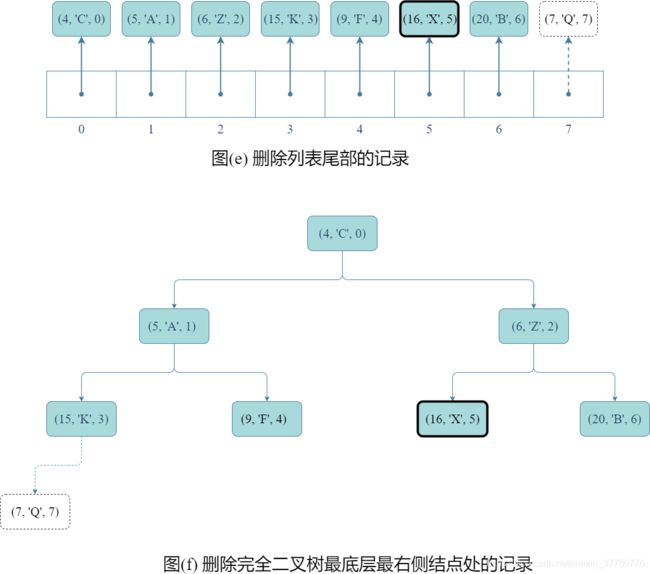
• 然后，如图(e)和(f)所示，删除列表尾部元素，实际上只要调用列表的pop()方法即可；

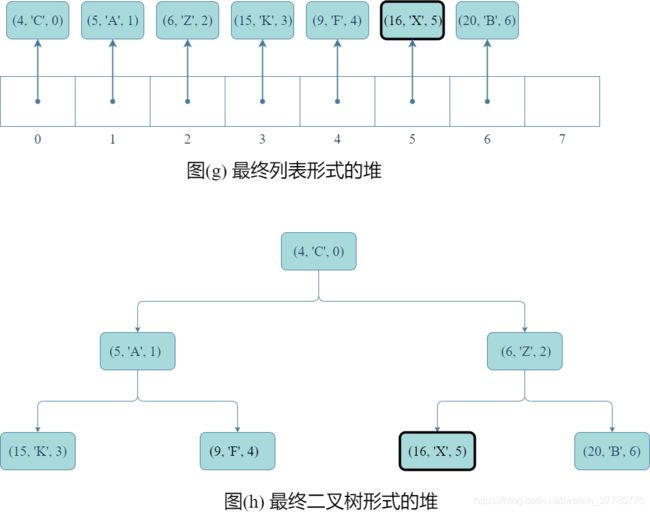
• 最后，得到如图(g)和(h)所示的结果。实际上，如果上述(e)和(f)所示步骤结束后完全二叉树不满足堆序性质，则还需像分析update()方法时一样，重复图©、(d)、(e)、(f)的步骤。

二、支持插队模型的优先级队列实现

基于上述分析，本节将通过继承【数据结构Python描述】树堆（heap）简介和Python手工实现及使用树堆实现优先级队列中实现的HeapPriorityQueue来实现支持插队模型的优先级队列AdaptablePriorityQueue。

Item

首先，需要对描述优先级队列中每一条记录的类_Item进行如下所示的升级

from heap_priority_queue import HeapPriorityQueue


class Item(HeapPriorityQueue._Item):
    """用于保存优先级队列每一条记录的键、值以及键值在列表中索引的类"""
    def __init__(self, key, value, idx):
        super().__init__(key, value)
        self.idx= idx

也就是说，后续优先级队列底层的列表保存的是一系列Item实例，每一个实例均保存了key、value以及当前实例在列表中的索引idx，对于用户向优先级队列中成功插入的每一对(key, value)，都会得到一个Item实例的引用，如图分析update()方法时提到中的cursor。

_swap(i, j)

在HeapPriorityQueue中实现过了该方法，此处需重写该方法使得(key, value, idx)形式的记录的idx域如实反应该记录当前在列表中的位置：

def _swap(self, i, j):
    """重写父类方法"""
    super()._swap(i, j)
    self._data[i].idx = i
    self._data[j].idx = j

_bubble(j)

由于调用update()方法之后，某结点处记录按照键的大小既可能需要下沉也可能需要上浮，因此将继承自HeapPriorityQueue的结点记录上浮方法（_upheap()）和下沉方法（_downheap()）封装进一个方法_bubble()中。

def _bubble(self, i):
    """
    对优先级队列的记录进行向上或向下冒泡，确保完全二叉树满足堆序性质
    :param i: 记录在列表中的索引
    :return: None
    """
    if i > 0 and self._data[i] < self._data[self._parent(i)]:
        self._upheap(i)
    else:
        self._downheap(i)

add(key, value)

该方法继承自HeapPriorityQueue，此处仅重写后返回新增记录的引用，供传入update()和remove()方法中使用：

def add(self, key, value):
    """
    重写父类方法，在实现父类方法功能的基础上，返回新增记录的引用
    :param key: 键
    :param value: 值
    :return: 新增Item对象的引用
    """
    cursor = self.Item(key, value, len(self._data))  # 封装键值对对象
    self._data.append(cursor)
    self._upheap(len(self._data) - 1)
    return cursor

update(item, key, value)

该方法需要最终调用上述_bubble()方法以确保最终的完全二叉树仍然是一个堆：

def update(self, item, key, value):
    """
    更新item的key和/或value
    :param item: Item类一个实例对象的引用
    :param key: 键
    :param value: 值
    :return: None
    """
    i = item.idx
    if not (0 <= i < len(self) and self._data[i] is item):
        raise ValueError('给定的Item实例无效！')
    item.key = key
    item.value = value
    self._bubble(i)

remove(item)

实现如下：

def remove(self, item):
    """
    删除item引用的对象，并返回(key, value)
    :param item: Item类一个实例对象的引用
    :return: (key, value)
    """
    i = item.idx
    if not (0 <= i < len(self) and self._data[i] is item):
        raise ValueError('给定的Item实例无效！')
    if i == len(self) - 1:  # 直接删除即可
        self._data.pop()
    else:
        self._swap(i, len(self) - 1)
        self._data.pop()
        self._bubble(i)
    return item.key, item.value

三、支持插队模型的优先级队列复杂度分析

针对上述实现的AdaptableHeapPriorityQueue，其各方法的最坏时间复杂度如下表所示：

ADT方法	时间复杂度
__len__(q)、q.is_empty()、q.min()	$O(1)$
p.add(key, value)	$O(log(n))$1
q.update(item, key, value)	$O(log(n))$
q.remove(item)	$(log(n))$1
q.remove_min()	$O(log(n))$1

四、支持插队模型的优先级队列代码测试

下面是使用上述实现的AdaptableHeapPriorityQueue模拟“银行VIP客户插队办理业务”及“被插队客户愤而离去”的完整代码：

# adaptable_heap_priority_quue.py
from heap_priority_queue import HeapPriorityQueue


class AdaptableHeapPriorityQueue(HeapPriorityQueue):
    """使用二叉堆实现的可进行Item实例删除和更新操作的优先级队列"""

    class Item(HeapPriorityQueue._Item):
        """用于保存优先级队列每一条记录的键、值以及键值在列表中索引的类"""

        def __init__(self, key, value, index):
            super().__init__(key, value)
            self.idx = index

    def _swap(self, i, j):
        """重写父类方法"""
        super()._swap(i, j)
        self._data[i].idx = i
        self._data[j].idx = j

    def _bubble(self, i):
        """
        对优先级队列的记录进行向上或向下冒泡，确保完全二叉树满足堆序性质
        :param i: 记录在列表中的索引
        :return: None
        """
        if i > 0 and self._data[i] < self._data[self._parent(i)]:
            self._upheap(i)
        else:
            self._downheap(i)

    def add(self, key, value):
        """
        重写父类方法，在实现父类方法功能的基础上，返回新增记录的引用
        :param key: 键
        :param value: 值
        :return: 新增Item对象的引用
        """
        cursor = self.Item(key, value, len(self._data))  # 封装键值对对象
        self._data.append(cursor)
        self._upheap(len(self._data) - 1)
        return cursor

    def update(self, item, key, value):
        """
        更新item的key和/或value
        :param item: Item类一个实例对象的引用
        :param key: 键
        :param value: 值
        :return: None
        """
        i = item.idx
        if not (0 <= i < len(self) and self._data[i] is item):
            raise ValueError('给定的Item实例无效！')
        item.key = key
        item.value = value
        self._bubble(i)

    def remove(self, item):
        """
        删除item引用的对象，并返回(key, value)
        :param item: Item类一个实例对象的引用
        :return: (key, value)
        """
        i = item.idx
        if not (0 <= i < len(self) and self._data[i] is item):
            raise ValueError('给定的Item实例无效！')
        if i == len(self) - 1:  # 直接删除即可
            self._data.pop()
        else:
            self._swap(i, len(self) - 1)
            self._data.pop()
            self._bubble(i)
        return item.key, item.value


if __name__ == '__main__':
    q = AdaptableHeapPriorityQueue()
    cursor1 = q.add(4, '愤愤不平普通客户')
    cursor2 = q.add(5, '普通客户1')
    cursor3 = q.add(6, '普通客户2')
    cursor4 = q.add(15, '普通客户3')
    cursor5 = q.add(9, '暂不知自己是VIP的土豪客户')
    cursor6 = q.add(7, '普通客户4')
    cursor7 = q.add(20, '普通客户5')
    cursor8 = q.add(16, '普通客户6')
    print(q)  # [(4, '愤愤不平普通客户'), (5, '普通客户1'), (6, '普通客户2'), (15, '普通客户3'), (9, '暂不知自己是VIP的土豪客户'), (7, '普通客户4'),
    # (20, '普通客户5'), (16, '普通客户6')]
    print('按上述顺序，下一个办理业务的应该是：', q.min()[1])  # 按上述顺序，下一个办理业务的应该是：愤愤不平普通客户
    q.update(cursor5, 1, '意识到自己是VIP的土豪客户')  # 修改cursor5引用的记录的优先级，即土豪插队
    print('VIP土豪插队后下一个办理业务的是：', q.min()[1])  # VIP土豪插队后下一个办理业务的是： 意识到自己是VIP的土豪客户
    q.remove(cursor1)  # '愤愤不平普通客户'要求删除自己取的号
    print(q)  # [(1, '意识到自己是VIP的土豪客户'), (5, '普通客户1'), (6, '普通客户2'), (15, '普通客户3'), (16, '普通客户6'), (7, '普通客户4'), (20, 
    # '普通客户5')] 

---

1. 经摊销后的最坏时间复杂度。 ↩︎ ↩︎ ↩︎