长期成本曲线为何是短期成本曲线包络线？——用包络定理证明

长期成本曲线及直观理解

微观经济学中常会提到长期总（平均）成本曲线是短期总（平均）成本曲线的包络线，如下图所示：

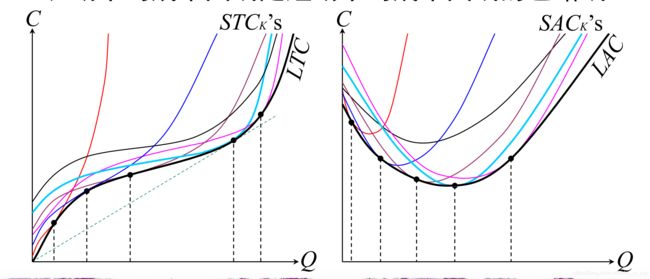
如何直观理解？
首先想，企业如何确定其长期成本曲线？首先看企业长期生产函数：$Q=F(K,L)$。在短期：$Q=F(\overline{K},L)$，即K不可调整，算作其固定成本。此处注意，在短期，K调整后，不仅固定成本会调整，其可变成本也会调整，可以写一个CD生产函数和短期可变成本函数SVC=wL，进而推导出SVC=f(Q,K)，也就是说K可以改变该曲线的系数。
根据理性人假设，在每个Q下，企业都要在约束下做成本最小化决策。在短期，同一个Q可以对应不同的SC（在不同的SVC曲线上，同一个Q上的点），这是因为短期生产决策还受K的约束。在短期，不同的K对应不同的SC曲线。而在长期，由于K可以调整，因此在每一个长期目标Q下，企业生产不受K的约束，在任一个Q都有时间调整K直到SC最小，以此时对应的K，L投入长期生产。对每一个Q对应的min(SC)连成一条线，就是长期成本曲线。现假设，若某一个Q处，出现了SC小于LC，则理性的企业在该点会调整K，使C减小，直到SC=LC。因此，LC把所有SC曲线都包了起来，不会有SC的点低于LC。包络曲线满足这样的要求。
当然，这样的直观理解只能证明包络曲线是长期成本曲线具有包络性质的充分条件，还没证明是必要条件。因此，下面用数学证明包络曲线是长期成本曲线具有特定性质的充分必要条件。

包络定理

包络定理讨论了无约束和有约束条件下的最优化。最简单的，考虑无约束最优化。设一个函数包含x,y两个变量和一个参数$\varphi$，需要求出这一函数的极小值：
$minU=f(x,y,\varphi )$
由一阶条件（x,y偏导=0）得出$x^{\ast }=x^{\ast }(\varphi )$，$y^{\ast }=y^{\ast }(\varphi )$，则U取极小值V时，有$V(\varphi )=f(x^{\ast },y^{\ast },\varphi )$。结合偏导=0，可以得出：
则$\frac{dV(\varphi )}{d\varphi }=$$\frac{\partial f(x,y,\varphi )}{\partial \varphi }{|}_{x=x^{\ast },y=y^{\ast }}$

使用包络定理证明

下面，给出问题的条件及设定：
长期（短期）成本函数：$C=wl+rk=g(k,l)$，企业生产函数：$q=f(k,l)$。则可以推出成本函数：$C=G(k,l,q)$。对于长期情况，给定某产量q，企业一定可以通过调整k和l至$k^{\ast }$，$l^{\ast }$，作出成本最小化生产决策，因此有$LC(q)=G(k^{\ast },l^{\ast },q)$。
短期成本函数即为：
$SC=G(k,l,q)$，k和l没有经过调整。
要证明的问题是，对于每一个Q，都有长期成本曲线在该点的导数=该Q下最优短期成本曲线在该点的导数。
用数学语言表述，要证明包络，即是证明：
$\frac{dLC(q)}{d(q)}=\frac{dS{C}^{\ast }(q)}{d(q)}$
其中，$S{C}^{\ast }(q)$是在q处所有可能的短期成本函数中，最低的函数，即k取$k^{\ast }(q)$，l取$l^{\ast }(q)$时的函数。
由包络定理，$\frac{dLC(q)}{dq}=$$\frac{dG(k^{\ast },l^{\ast },q)}{dq}=$ $\frac{\partial G(k,l,q)}{\partial q}{|}_{k=k^{\ast },l=l^{\ast }}=\frac{dS{C}^{\ast }(q)}{d(q)}$

至此，$\frac{dLC(q)}{d(q)}=\frac{dS{C}^{\ast }(q)}{d(q)}$得证。