动态规划整理

1.最长连续序列。比如  abccccfa,最长连续序列为cccc，长度为4

思路：另开一个数组记录到目前位置最长连续序列长度。每个位置的字符（除第一个）和前一个比较，相同+1，不同标为1

图示：

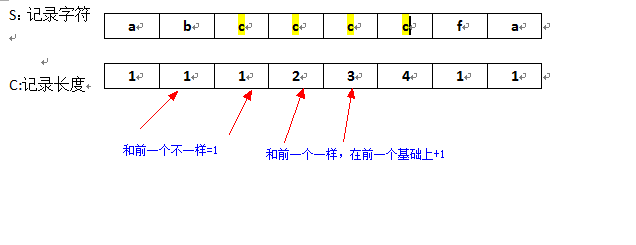
代码：

#include <stdio.h>

#include <string.h>

int main()

{

    char s[10] = "abccccfa";

    int num[10] = {0};

    char tmp;

    int maxpos, maxval, i;



    num [0] = 1;

    maxpos = 0;

    tmp = s[0];

    for(i = 1; i <strlen(s); i++)

    {

        if (s[i] == tmp)

            num[i] = num[i-1] + 1;

        else

            num[i] = 1;

        if(num[i] > num[maxpos])

            maxpos = i;

        tmp = s[i];

    }

    printf("maxlen:%d***maxchar:%c\n", num[maxpos], s[maxpos]);

    return 0;

}

结果：

分析： 空间复杂度：O(n)  时间复杂度：O(n)

同思路问题：

（1）求一字母序列的最长连续上升序列的长度（比如abcffgmnE，abc长为3）

    思路：构造一同样大小的数组来记录到目前为止的最长连续序列的长度。在确定该位置的长度是，和前一个比较，如果ascii吗相减为1，那么在上一个长度的基础上+1；否则直接赋值1。

（2）求数字序列的最长连续上升序列的和（比如34123480，1234和为10）

    思路：构造一同样大小的数组来记录到目前为止的最长连续序列的和。在确定该位置的和是，和前一个比较，如果相差1，那么在上一个和的基础上+该位置原数组的值；否则直接复制该位置原数组的值。

（3）数列中最大连续元素之和（比如：3 -2 5 1 -10，最大元素之和为7（3 -2 5 1））

int MaxSubSum(int *arr,int n)

{

    int tmp = 0;

    int MAX = arr[0];

    for(int i = 0 ; i < n ; i++)

    {

        tmp += arr[i];

        if(tmp < 0)

        {

            tmp = 0;

        }

        if(MAX < tmp)

        {

            MAX = tmp;

        }

    }

    return MAX;

View Code

 

2.最大上升序列的长度 （如：“amnpabpzjoq” 的最大上升序列 为："amnpz" 长度为5）

图示：

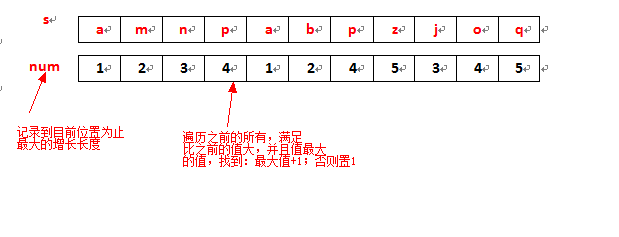
代码：

#include <stdio.h>

#include <string.h>

int main()

{

    char s[] = "amnpabpzjoq";

    int num[100] = {0};

    

    int maxnum, i, j;



    for(i = 0; i < strlen(s); i++)

    {

        maxnum = -1;

        for(j = i-1; j >=0; j--)

        {

            if (s[i] > s[j] && num[j] > maxnum)

                maxnum = num[j];

        }

        if (maxnum == -1)

            num[i] = 1;

        else

            num[i] = maxnum + 1;

    }

    maxnum = num[0];

    for (i = 1; i < strlen(s); i++)

    {

        printf("%d\n", num[i]);

        if (num[i] > maxnum)

            maxnum = num[i];

    }



    printf("maxlen:%d\n", maxnum);

}

结果：

  3. 编辑距离

定义：字符串a只能通过“替换、插入、删除”三种操作得到字符串b，期间所做操作的次数。

例如：abc ——> cb，编辑距离为2。执行的操作：a替换为c，删除字符c.

思路：二维数组记录到字符a的m位置和字符串b的n位置，编辑距离f(m, n)。

       f(m, n) = min(f(m-1, n)+1, f(m, n-1)+1, f(m-1, n-1)+same(m, n))， 其中same(m,n)指字符串a的第m个字符是否等于字符串b的第n个字符，等为0，否则为1.

注意： 空和字串的相似程度时，距离为别的字串的长度！

图示：

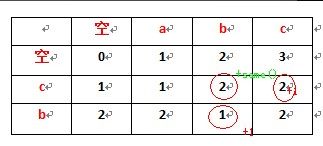
代码：

#include <stdio.h>

#include <string.h>

int minvalue(int a, int b, int c)

{

    int min = a > b ? b : a;

    min = min > c ? c : min;

    return min;

}

int same(int a, int b)

{

    if (a != b)

        return 1;

    else 

        return 0;

}

int main()

{

    char a[] = "bca";

    char b[] = "abc";

    int lena = strlen(a);

    int lenb = strlen(b);

    int c[lena+1][lenb+1], i, j;

    for(i=0; i <= lena; i++)

        c[i][0] = i;    

    for(i=0; i <= lenb; i++)

        c[0][i] = i;

    for(i = 1; i <= lena; i++)

        for(j=1; j <= lenb; j++)

            c[i][j] = minvalue(c[i-1][j]+1, c[i][j-1]+1, (c[i-1][j-1]+same(a[i], b[j])));

    for(i=0; i <= lena; i++)

    {

        for(j=0; j <= lenb; j++)

            printf("%d\t", c[i][j]);

        printf("\n");

    }

    printf("Lavenshtein distance:%d\n", c[lena][lenb]); 

    return 0;

}

执行结果：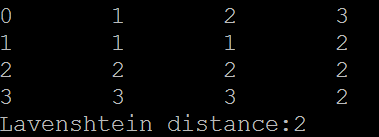

同思路问题：

1.最长公共子序列：详见：http://www.cnblogs.com/kaituorensheng/archive/2013/03/31/2992319