POI-step traversing a tree 树的隔三遍历(题目)
http://smalloj.com/problem.php?pid=19
Step Traversing a Tree
| Time Limit: | 1000ms | Memory Limit: | 64000KiB |
| Accepted: | 0 | Submitted: | 0 |
POI II Stage 3 Problem 2
Step Traversing a Tree
A graph is a pair (V, E), where V is a finite set of elements called vertices of the graph, and E is a subset of the set of all unordered pairs of distinct vertices. The elements of the set E are called edges of the graph. If for each pair of distinct vertices u, v there exists exactly one sequence of distinct vertices w0, w1, ..., wk, such that w0 = u, wk = v and the pairs {wi, wi + 1} are in E, for i = 0, ..., k - 1, then the graph is called a tree. We say that the distance between the vertices u and v in the tree is k.
It is known that a tree of n vertices has exactly n - 1 edges. A tree T whose vertices are numbered from 1 to n can be unambiguously described by giving the number of its vertices n, and an appropriate sequence of n - 1 pairs of positive integers describing its edges.
Any permutation of vertices - i.e. a sequence in which each vertex appears exactly once - is called a traversing order of a tree. If the distance of each two consecutive vertices in some order of the tree T is at most c, then we say that it is a traversing order of the tree with step c.
It is known that for each tree its traversing order with step 3 can be found.
Example
The picture shows a tree of 7 vertices. The vertices are represented by black dots, and edges by line segments joining the dots.
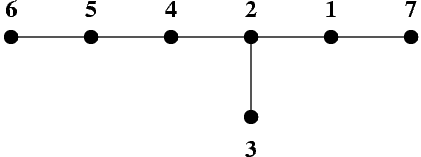
This tree can be traversed with step 3 by visiting its vertices in the following order: 7 2 3 5 6 4 1.
Task
Write a program that:
- reads a description of a tree from the text file DRZ.IN,
- finds an arbitrary traversing order of that tree with step 3,
- writes that order in the text file DRZ.OUT.
Input
- In the first line of the file DRZ.IN there is a positive integer n, not greater than 5000 - it is the number of vertices of the tree.
- In each of the following n - 1 lines there is one pair of positive integers separated by a single space and representing one edge of the tree.
Output
In the successive lines of the file DRZ.OUT one should write the numbers of the successive vertices in a traversing order of the tree with step 3 - each number should be written in a separate line.
Example
The following file DRZ.IN is a correct description of the tree presented in the picture:
7 1 2 2 3 2 4 4 5 5 6 1 7
The following file DRZ.OUT is a correct solution:
7 2 3 5 6 4 1