K-means算法和矢量量化
语音信号的数字处理课程作业——矢量量化。这里采用了K-means算法,即假设量化种类是已知的,当然也可以采用LBG算法等,不过K-means比较简单。矢量是二维的,可以在平面上清楚的表示出来。
1. 算法描述
本次实验选择了K-means算法对数据进行矢量量化。算法主要包括以下几个步骤
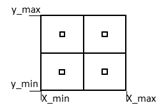
- 初始化:载入训练数据,确定初始码本中心(4个);
- 最近邻分类:对训练数据计算距离(此处采用欧式距离),按照距离最小分类;
- 码本更新:重新生成包腔对应的质心;
- 重复分类和码本更新步骤,知道达到最大迭代次数或满足一定停止准则;
- 利用上述步骤得到的码本对测试数据进行矢量量化,并求最小均方误差。
本实验准备使用MATLAB软件完成矢量量化任务,具体步骤实现如下
- 将training.dat和to_be_quantized.dat置于当前工作文件夹内,采用load命令载入training.dat 。
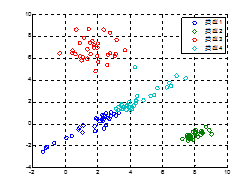
- 采用合适的规则选取初始的码本中心。如图 1所示。
- 计算训练数据和每一码本中心之间的距离。
- 采用最近邻准则进行分类。
- 重新计算质心,计算公式如下所示。
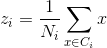
- 重复3~5,直到满足最大迭代次数或是两次迭代结果没有发生改变时,此时结果为训练结果。
- 利用训练结果对to_be_quantized.dat进行矢量量化。
2. 代码
MATLAB代码如下
1 %% training 2 load('training.dat'); 3 scatter(training(:,1),training(:,2)); 4 %初始中心选取 5 x_max = max(training(:,1)); 6 x_min = min(training(:,1)); 7 y_max = max(training(:,2)); 8 y_min = min(training(:,2)); 9 z1 = [(3*x_min+x_max)/4 (3*y_min+y_max)/4]; 10 z2 = [(3*x_max+x_min)/4 (3*y_min+y_max)/4]; 11 z3 = [(3*x_min+x_max)/4 (3*y_max+y_min)/4]; 12 z4 = [(3*x_max+x_min)/4 (3*y_max+y_min)/4]; 13 z = [z1;z2;z3;z4]; 14 hold on; 15 scatter(z(:,1),z(:,2)); 16 legend('训练数据','码本');grid on; 17 hold off; 18 for k = 1:20 19 %码本分类,欧式距离 20 distancetoz1 = (training - repmat(z1,size(training,1),1)).^2; 21 distancetoz1 = sum(distancetoz1,2); 22 distancetoz2 = (training - repmat(z2,size(training,1),1)).^2; 23 distancetoz2 = sum(distancetoz2,2); 24 distancetoz3 = (training - repmat(z3,size(training,1),1)).^2; 25 distancetoz3 = sum(distancetoz3,2); 26 distancetoz4 = (training - repmat(z4,size(training,1),1)).^2; 27 distancetoz4 = sum(distancetoz4,2); 28 distance = [distancetoz1 distancetoz2 distancetoz3 distancetoz4]; 29 % 分类 30 if(classification == (distance == repmat(min(distance,[],2),1,4))) 31 error = mean(min(distance,[],2)); 32 break; %如果两次迭代之间没有变化,结束迭代 33 end; 34 classification = (distance == repmat(min(distance,[],2),1,4)); 35 c1 = training(classification(:,1),:); 36 c2 = training(classification(:,2),:); 37 c3 = training(classification(:,3),:); 38 c4 = training(classification(:,4),:); 39 figure;scatter(c1(:,1),c1(:,2));hold on;scatter(c2(:,1),c2(:,2)); 40 scatter(c3(:,1),c3(:,2));scatter(c4(:,1),c4(:,2)); 41 legend('类型1','类型2','类型3','类型4');grid on;hold off; 42 % 码本更新 43 z1 = mean(c1); 44 z2 = mean(c2); 45 z3 = mean(c3); 46 z4 = mean(c4); 47 z = [z1;z2;z3;z4]; 48 end 49 %% Test 50 load('to_be_quantized.dat') 51 distancetoz1 = (to_be_quantized - repmat(z1,size(to_be_quantized,1),1)).^2; 52 distancetoz1 = sum(distancetoz1,2); 53 distancetoz2 = (to_be_quantized - repmat(z2,size(to_be_quantized,1),1)).^2; 54 distancetoz2 = sum(distancetoz2,2); 55 distancetoz3 = (to_be_quantized - repmat(z3,size(to_be_quantized,1),1)).^2; 56 distancetoz3 = sum(distancetoz3,2); 57 distancetoz4 = (to_be_quantized - repmat(z4,size(to_be_quantized,1),1)).^2; 58 distancetoz4 = sum(distancetoz4,2); 59 distance = [distancetoz1 distancetoz2 distancetoz3 distancetoz4]; 60 testerror = mean(min(distance,[],2)); 61 62 classification = (distance == repmat(min(distance,[],2),1,4)); 63 c1 = to_be_quantized(classification(:,1),:); 64 c2 = to_be_quantized(classification(:,2),:); 65 c3 = to_be_quantized(classification(:,3),:); 66 c4 = to_be_quantized(classification(:,4),:); 67 figure;scatter(c1(:,1),c1(:,2));hold on;scatter(c2(:,1),c2(:,2)); 68 scatter(c3(:,1),c3(:,2));scatter(c4(:,1),c4(:,2)); 69 legend('类型1','类型2','类型3','类型4');grid on;hold off;
3. 实验结果
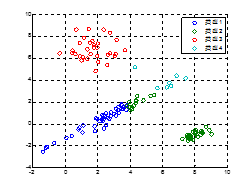
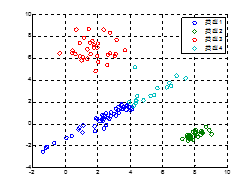
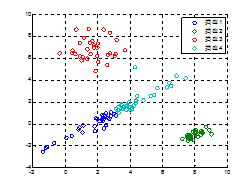
图 3第一次迭代结果 图 4第四次迭代结果
图 5第八次迭代结果 图 6第九次迭代结果
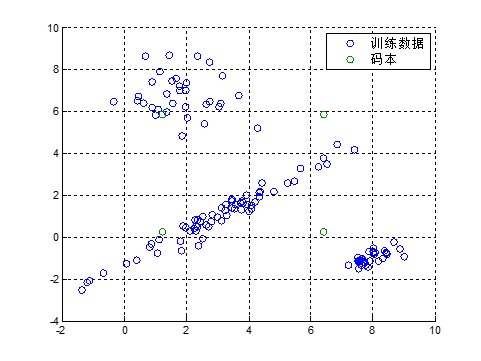
图 2展示了训练数据的分布,图 3~6是迭代过程中分类的变化情况,迭代完成后的码本为
- Z1 = [1.62060631541935 -0.108624145483871]
- Z2 = [7.96065094375000 -0.999061308437500]
- Z3 = [1.72161941468750 6.82121444062500]
- Z4 = [4.43652765757576 2.18874305151515]
4. 实验数据
training.dat

1 8.4416189e+000 -7.9885975e-001 2 1.1480908e+000 7.8735044e+000 3 7.7380144e+000 -1.2165061e+000 4 8.9727144e-001 7.3962468e+000 5 7.5343823e+000 -1.1424504e+000 6 -6.9234039e-001 -1.7096610e+000 7 7.6418740e+000 -1.3563792e+000 8 3.1091418e+000 6.3850541e+000 9 2.3482174e+000 4.7553506e-001 10 -1.3840364e+000 -2.5480394e+000 11 8.2008897e+000 -1.1448387e+000 12 -1.1392497e+000 -2.0809884e+000 13 3.7970116e+000 1.6906469e+000 14 3.4484200e+000 1.3980911e+000 15 2.5701485e+000 5.3755044e+000 16 8.3899076e+000 -6.6675309e-001 17 2.0146545e+000 5.6984592e+000 18 1.8853328e+000 5.2762628e-001 19 5.6781432e+000 3.2588691e+000 20 1.0102480e+000 5.8167707e+000 21 7.7302763e+000 -1.2030348e+000 22 4.2118845e+000 1.6527181e+000 23 4.3920049e-001 6.7168970e+000 24 8.1934984e-001 -5.1917945e-001 25 4.3708769e+000 2.1613573e+000 26 1.8569681e+000 4.8380565e+000 27 3.4732504e+000 1.7953635e+000 28 7.5822756e+000 -1.1521814e+000 29 2.6434078e+000 6.3295690e+000 30 1.9968582e+000 7.3529314e+000 31 4.0833513e+000 1.4936002e+000 32 3.6767894e+000 6.7446912e+000 33 1.3524515e+000 6.8177858e+000 34 3.9711504e+000 1.5452503e+000 35 1.5594711e+000 6.3885281e+000 36 3.4692089e+000 1.7118124e+000 37 5.2575491e+000 2.5601553e+000 38 7.8827882e+000 -6.8867840e-001 39 4.8176593e+000 2.1684005e+000 40 2.7402486e+000 8.3320174e+000 41 2.2549011e+000 3.9393641e-001 42 8.0840542e+000 -7.3155184e-001 43 8.8753667e-001 6.1607892e+000 44 1.8067727e+000 -2.1099454e-001 45 6.8650914e+000 4.4228389e+000 46 6.4174056e+000 3.7590081e+000 47 4.0933273e+000 1.3598676e+000 48 2.2882999e+000 5.1876795e-001 49 7.9225523e+000 -1.1725456e+000 50 4.3561335e+000 1.8976163e+000 51 8.3279098e+000 -1.0232899e+000 52 6.2551331e+000 3.3449949e+000 53 3.1276024e+000 7.8463356e-001 54 6.5241605e+000 3.4561490e+000 55 4.1588140e-001 6.4974858e+000 56 2.7379263e+000 6.4746080e+000 57 7.2185639e+000 -1.3525589e+000 58 7.5424890e+000 -1.5317814e+000 59 3.7468423e+000 1.6110753e+000 60 8.8708536e+000 -5.6439331e-001 61 7.6960713e+000 -1.1960633e+000 62 7.5979552e+000 -1.1469059e+000 63 2.8220978e+000 1.0360184e+000 64 3.8165165e+000 1.6082223e+000 65 6.6799248e-002 -1.2910367e+000 66 2.3054028e+000 2.8450986e-001 67 4.2788715e+000 5.1995858e+000 68 3.0006534e+000 9.1250414e-001 69 7.6051326e+000 -1.1005476e+000 70 2.5331653e+000 9.7428007e-001 71 1.0743104e+000 6.0859296e+000 72 6.7237149e-001 8.6117274e+000 73 2.4333003e+000 7.1421389e-001 74 1.7723473e+000 7.1841833e+000 75 3.5762796e+000 1.5348648e+000 76 2.7863558e+000 7.3565043e-001 77 8.0284284e+000 -7.9636983e-001 78 8.4672682e+000 -8.2062254e-001 79 2.3519727e+000 8.1632796e-001 80 7.4240720e+000 4.1800229e+000 81 1.9724319e+000 4.4328699e-001 82 7.7622621e+000 -1.3506605e+000 83 2.3793018e+000 -4.3107386e-001 84 3.2455220e+000 1.2697488e+000 85 1.3644859e+000 5.9712644e+000 86 5.4815655e+000 2.6608754e+000 87 -1.2002073e+000 -2.1765731e+000 88 -3.5558595e-001 6.4387512e+000 89 3.9418185e+000 1.9858047e+000 90 1.0533626e+000 -7.9068285e-001 91 1.9560213e+000 6.2001316e+000 92 7.5555203e+000 -1.2087337e+000 93 1.7851705e+000 7.0073148e+000 94 2.2736274e+000 7.9336349e-001 95 7.6615799e+000 -1.0445564e+000 96 2.7181608e+000 4.7615418e-001 97 1.8291149e+000 -6.7261971e-001 98 7.8640867e+000 -1.4296092e+000 99 2.6362814e+000 5.8303048e-001 100 3.7771102e+000 1.2928196e+000 101 7.5360359e+000 -9.7942712e-001 102 4.0257498e+000 1.2217666e+000 103 8.4500853e+000 -7.6599648e-001 104 3.0488646e+000 6.2159289e+000 105 2.0954150e+000 2.5848825e-001 106 1.6592148e+000 7.5650162e+000 107 3.5535363e+000 1.3326217e+000 108 4.3388636e+000 2.1235893e+000 109 3.1233524e+000 1.3971470e+000 110 7.6317385e+000 -1.0744610e+000 111 8.5028402e-001 -3.2822876e-001 112 8.6903131e+000 -2.6843242e-001 113 4.4418011e+000 2.5676053e+000 114 2.5119872e+000 -1.0521242e-001 115 1.9613752e+000 7.0072931e+000 116 3.2607143e+000 1.5432286e+000 117 3.2830401e+000 1.0228031e+000 118 8.0201528e+000 -7.0827461e-001 119 3.1597313e+000 7.6750043e+000 120 9.0059933e+000 -9.6130246e-001 121 1.1037820e+000 -1.2980812e-001 122 1.5334911e+000 7.4282719e+000 123 6.0948533e-001 6.3861341e+000 124 4.0065706e-001 -1.1015776e+000 125 2.3451558e+000 8.6384057e+000 126 1.4490876e+000 8.6646066e+000 127 8.0421821e+000 -8.1100509e-001 128 8.0175747e+000 -5.6119093e-001
to_be_quantized

1 3.7682247e+000 8.3609865e-001 2 2.6963398e+000 6.5766226e-001 3 3.3438207e+000 1.2495321e+000 4 1.3646195e+000 -6.3947640e-001 5 7.8227583e+000 -8.8616996e-001 6 1.3532508e+000 7.6607304e+000 7 2.2741739e+000 6.9387226e+000 8 3.5361382e+000 5.9729821e+000 9 8.0409138e+000 -1.1234886e+000 10 7.9630460e+000 -1.3032200e+000 11 2.3478158e+000 6.9759690e+000 12 3.2632942e+000 1.5675470e+000 13 1.5241488e+000 7.1053147e+000 14 5.7320838e+000 3.4042655e+000 15 2.3339411e+000 6.9428434e+000 16 6.5330392e+000 3.4415860e+000 17 3.1068803e+000 8.0080363e+000 18 7.4078126e+000 -1.3416027e+000 19 1.9925474e+000 -2.7782790e-001 20 5.0187915e+000 2.7058427e+000 21 2.6535497e-001 -1.2622069e+000 22 1.4960584e+000 6.3355004e+000 23 3.1933474e-001 7.1467466e+000 24 8.2821020e+000 -9.5178778e-001 25 2.5653586e+000 6.9836115e+000 26 3.6937139e+000 1.1535671e+000 27 8.5390043e+000 -5.0678923e-001 28 7.5436898e-001 -6.7669379e-001 29 2.1638213e+000 7.6142401e+000 30 4.8522826e+000 2.7079076e+000 31 5.4890641e+000 3.3875394e+000 32 4.2525899e+000 1.8861744e+000 33 8.4088615e+000 -1.1920963e+000 34 5.5396960e+000 2.9680110e+000 35 3.3334381e+000 1.4384861e+000 36 3.5212919e+000 1.0327602e+000 37 4.6303492e+000 2.1627805e+000 38 3.9385929e+000 1.0010804e+000 39 8.4553633e+000 -7.2297277e-001 40 1.8111095e+000 7.6132396e+000 41 1.1240984e+000 -2.7029879e-001 42 -3.3840083e-002 -1.5590834e+000 43 7.1674870e+000 -1.5449905e+000 44 8.5103026e+000 -9.8820393e-001 45 7.7529857e+000 -1.4787432e+000 46 1.8704913e+000 6.9370116e+000 47 6.0271939e+000 3.2118915e+000 48 2.8287461e+000 7.3399383e+000 49 4.1568876e+000 1.5631238e+000 50 8.2187067e-001 -5.8546437e-001 51 3.1084965e+000 5.3512449e+000 52 4.1581386e+000 2.1763345e+000 53 3.2267474e+000 1.4105815e+000 54 8.1564752e-001 7.2540175e+000 55 8.0241402e+000 -8.2411742e-001 56 6.2773554e+000 3.1729045e+000 57 8.5460058e+000 -1.0330056e+000 58 8.6215210e+000 -7.4057378e-001 59 7.4872291e+000 -1.0113921e+000 60 3.3155133e+000 9.7636038e-001 61 2.1051593e+000 3.4894654e-001 62 3.6776134e+000 1.5387928e+000 63 2.9009105e+000 5.6931589e+000 64 8.0567164e+000 -1.0000803e+000