Learn Prolog Now 翻译 - 第三章 - 递归 - 第三节,练习题和答案
练习题3.1
在之前的章节中,我们已经讨论了如下的谓词逻辑:
descend(X, Y) :- child(X, Y).
descend(X, Y) :- child(X, Z), descend(Z, Y).
假设我们将谓词逻辑重构如下:
descend(X, Y) :- child(X, Y).
descend(X, Y) :- descend(X, Z), descend(Z, Y).
这会导致问题吗?
我的答案:
1. 这个谓词逻辑是有问题的,因为规则2中存在左递归的情况,即规则2的主干部分的第一个目标,和规则2的头部是相同的函子;
2. 但是由于规则1是一个非递归的谓词逻辑,所以在进行一些查询时,能够根据这个规则进行终止,从而得出结果,比如:
?- descend(anne, bridget).
Prolog会回答true;
?- descend(anne, emily).
Prolog会回答true;
3. 但是在问一些不能由规则1终止的问题时,Prolog会报"Out of local stack"的错误,代表递归不能终止,比如:
?- descend(bridget, anne).
?- descend(anne, X); 一直使用“;”寻找下一个答案,也会报错
练习题3.2
知道俄罗斯木偶(又称为俄罗斯套娃娃)吗?其中较大的娃娃会包含较小的娃娃,如下图所示:
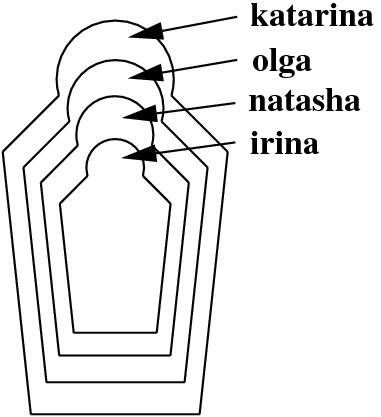
首先,写出一个使用谓词逻辑directlyIn/2的知识库,表示木偶直接被另外一个木偶包含。其次,定义一个递归的谓词逻辑in/2,告诉某个木偶是否被另外一个木偶包含
(直接或者间接)。比如,如果查询in(katarina, natasha),应该回答true,但是in(olga, katarina)应该回答false。
我的答案:
directlyIn(katarina, olga). directlyIn(olga, natasha). directlyIn(natasha, irina). in(X, Y) :- directlyIn(X, Y). in(X, Y) :- directlyIn(X, Z), in(Z, Y).
练习题3.3
有如下的知识库:
directTrain(saarbruecken, dudweiler).
directTrain(forbach, saarbruecken).
directTrain(freyming, forbach).
directTrain(stAvold, freyming).
directTrain(fahlquemont, stAvold).
directTrain(metz, fahlquemont).
directTrain(nancy, metz).
即,这个知识库记录了可以直接连通到城镇。但是,我们可以通过连接不同的城镇去旅行到更远的地方。请写一个谓词逻辑travelFromTo/2,可以告诉我们如何在这些
城镇之间通行。比如,如果查询:
?- travelFromTo(nancy, saarbruecken).
Prolog会回答true。
我的答案:
travelFromTo(X, Y) :- directTrain(X, Y).
travelFromTo(X, Y) :- directTrain(X, Z), travelFromTo(Z, Y).
练习题3.4
定义一个谓词逻辑greater_than/2,有两个参数,使用本章中的数字表示方法(比如,numeral(0), numeral(succ(0)), numeral(succ(succ(0)))等),然后判断第一
个参数是否大于第二个参数,比如:
?- greater_than(numeral(succ(succ(succ(0)))), numeral(succ(0))).
Prolog会回答true;
?- greater_than(numeral(succ(succ(0))), numeral(succ(succ(succ(0))))).
Prolog会回答false;
我的答案:
numeral(0). numeral(succ(X)) :- numeral(X). greater_than(numeral(X), numeral(0)) :- X \= 0. greater_than(numeral(succ(X)), numeral(succ(Y))) :- greater_than(numeral(X), numeral(Y))
练习题3.5
二叉树是每个内部节点严格有两个子节点的树形结构。一颗最小的二叉树仅由一个叶子节点构成。我们使用leaf(Label)代表叶子节点。比如,leaf(3)和leaf(7)都是
叶子节点。假设两颗二叉树B1和B2能够通过谓词tree/2,合并称为一颗二叉树,如下:tree(B1, B2)。那么,从叶子节点开始,我们能够构建二叉树:tree(leaf(1),leaf(2)),
类似地,从一颗二叉树tree(leaf(1),leaf(2))和叶子节点leaf(4),能够构建出新的二叉树:tree(tree(leaf(1),leaf(2)), leaf(4))。
现在,请定义一个谓词逻辑swap/2,能够根据第一个参数的二叉树,构建第二个参数成为其镜像二叉树,比如:
?- swap(tree(tree(leaf(1),leaf(2)), leaf(4)), T).
T = tree(leaf(4), tree(leaf(2),leaf(1))).
true
我的答案和解释,测试结果如下:
tree(leaf(X), leaf(Y)) :- integer(X), integer(Y). tree(tree(X1, X2), leaf(Y)) :- tree(X1, X2), integer(Y). tree(leaf(Y), tree(X1, X2)) :- integer(Y), tree(X1, X2). tree(tree(X1, X2), tree(Y1, Y2)) :- tree(X1, X2), tree(Y1, Y2). swap(tree(leaf(X1), leaf(X2)), tree(leaf(X2), leaf(X1))) :- integer(X1), integer(X2). swap(tree(Tree1, leaf(X1)), tree(leaf(X1), Tree2)) :- integer(X1), swap(Tree1, Tree2). swap(tree(leaf(X1), Tree1), tree(Tree2, leaf(X1))) :- integer(X1), swap(Tree1, Tree2). swap(tree(Tree1, Tree2), tree(Tree3, Tree4)) :- swap(Tree1, Tree4), swap(Tree2, Tree3).
一些说明:
1. integer/1谓词逻辑用于检查参数是否是一个整数;
2. tree/2谓词逻辑定义了二叉树的逻辑,分为四个子句:子句1定义了两个节点都是叶子节点的基础逻辑;子句2定义了左节点是二叉树,右节点是叶子节点的递归逻辑;
子句3定义了左节点是叶子节点,右节点是二叉树的递归逻辑;子句4定义了两个子节点都是二叉树的递归逻辑;
3. swap/2谓词逻辑定义了二叉树镜像实现,方式类似于tree/2的定义。
4. 下面是一些测试和结果:
?- swap(tree(leaf(1), leaf(2)), T).
T = tree(leaf(2), leaf(1)) .
?- swap(tree(tree(leaf(1), leaf(2)), leaf(4)), T).
T = tree(leaf(4), tree(leaf(2), leaf(1))) .
?- swap(tree(leaf(4), tree(leaf(1), leaf(2))), T).
T = tree(tree(leaf(2), leaf(1)), leaf(4)) .
?- swap(tree(tree(leaf(1), leaf(2)), tree(leaf(3), leaf(4))), T).
T = tree(tree(leaf(4), leaf(3)), tree(leaf(2), leaf(1))) .