前面写了一篇的文章,实现的方法是用的递归思想遍历,这篇文章主要介绍一下如何使用 压栈 的思想来遍历二分搜索树。
1.栈
为了更好的结合压栈的思想,下面先来介绍一下 栈 数据结构的知识:
1.1 栈的特点
- 栈是一种线性数据结构。
- 栈只能从一端添加数据,也只能从同一端取出元素,每次删除的元素都是最后入栈的元素。
- 入栈的元素具有后进先出的特点,即 Last In First Out(LIFO)。
- 栈顶处理方法通常有
入栈(push)、出栈(pop)、查看栈顶(peek)。 - 若是用
链表数据结构实现的栈,在栈顶会有一个栈顶指针。 栈这种数据结构的应用举例,如:可以实现撤销(undo)、程序的调用(系统栈)
1.2 栈的图示
1.3 链表的实现
这是封装好的一个链表类,能实现链表的基本功能:
null
* LinkedList constructor.
*/
public function __construct() {
$this->dummyHead = new Node(null, null);
$this->size = 0;
}
/**
* 获取链表大小
* @return int
*/
public function getSize(): int {
return $this->size;
}
/**
* 判断链表是否为空
* @return bool
*/
public function isEmpty(): bool {
return $this->size == 0;
}
/**
* 在链表的第 index 位置添加元素
* @param int $index
* @param $e
*/
public function add(int $index, $e): void {
if ($index < 0 || $index > $this->size) {
echo "索引范围错误";
exit;
}
$prve = $this->dummyHead;
for ($i = 0; $i < $index; $i++) {
$prve = $prve->next;
}
//将上插入位置的上一个位置的 next 节点指向插入节点,插入节点的 next 节点信息指向原上节点的 next 节点
$prve->next = new Node($e, $prve->next);
$this->size++;
}
/**
* 向链表开头添加元素
* @param $e
*/
public function addFirst($e): void {
$this->add(0, $e);
}
/**
* 向链表末尾添加元素
* @param $e
*/
public function addLast($e): void {
$this->add($this->size, $e);
}
/**
* 获取链表第 index 位置元素
* @param $index
*/
public function get($index) {
if ($index < 0 || $index > $this->size) {
echo "索引范围错误";
exit;
}
$node = $this->dummyHead;
for ($i = 0; $i < $index + 1; $i++) {
$node = $node->next;
}
return $node->e;
}
/**
* 获取链表第一个元素
* @return mixed
*/
public function getFirst() {
return $this->get(0);
}
/**
* 获取链表最后一个元素
* @return mixed
*/
public function getLast() {
return $this->get($this->size - 1);
}
/**
* 修改链表中第 index 位置元素值
* @param $index
* @param $e
*/
public function update($index, $e) {
if ($index < 0 || $index > $this->size) {
echo "索引范围错误";
exit;
}
$node = $this->dummyHead;
for ($i = 0; $i < $index + 1; $i++) {
$node = $node->next;
}
$node->e = $e;
}
/**
* 判断链表中是否存在某个元素
* @param $e
* @return bool
*/
public function contains($e): bool {
for ($node = $this->dummyHead->next; $node != null; $node = $node->next) {
if ($node->e == $e) {
return true;
}
}
return true;
}
/**
* 删除链表中第 index 位置元素
* @param $index
*/
public function remove($index) {
if ($index < 0 || $index > $this->size) {
echo "索引范围错误";
exit;
}
if ($this->size == 0) {
echo "链表已经是空";
exit;
}
$prve = $this->dummyHead;
for ($i = 0; $i < $index; $i++) {
$prve = $prve->next;
}
$node = $prve->next;
$prve->next = $node->next;
$this->size--;
return $node->e;
}
/**
* 删除链表头元素
*/
public function removeFirst() {
return $this->remove(0);
}
/**
* 删除链表末尾元素
*/
public function removeLast() {
return $this->remove($this->size - 1);
}
/**
* 链表元素转化为字符串显示
* @return string
*/
public function toString(): string {
$str = "";
for ($node = $this->dummyHead->next; $node != null; $node = $node->next) {
$str .= $node->e . "->";
}
return $str . "null";
}
}
class Node
{
public $e;//节点元素
public $next; //下个节点信息
/**
* 构造函数 设置节点信息
* Node constructor.
* @param $e
* @param $next
*/
public function __construct($e, $next) {
$this->e = $e;
$this->next = $next;
}
}1.4 调用链表实现的栈
这是一个封装好的 栈(Stack) ,通过实例化 链表类(LinkedList) 实现了入栈(push)和 出栈(pop),还有查看栈顶(peek):
array = new LinkedList();
}
/**
* 获取栈大小
* @return int
*/
public function getSize(): int {
return $this->array->getSize();
}
/**
* 判断栈是否为空
* @return bool
*/
public function isEmpty(): bool {
return $this->array->isEmpty();
}
/**
* 元素入栈
*/
public function push($e): void {
$this->array->addFirst($e);
}
/**
* 出栈
* @return mixed
*/
public function pop() {
return $this->array->removeFirst();
}
/**
* 查看栈顶元素
* @return mixed
*/
public function peek() {
return $this->array->getFirst();
}
/**
* 将栈数组转化为字符串
* @return string
*/
public function toString(): string {
return $this->array->toString();
}
}2.二分搜索树压栈思想实现前序遍历
2.1 节点定义
2.3 PHP 代码定义节点
class Node
{
public $e;
public $left = null;
public $right = null;
/**
* 构造函数 初始化节点数据
* Node constructor.
* @param $e
*/
public function __construct($e) {
$this->e = $e;
}
}2.2 原理说明
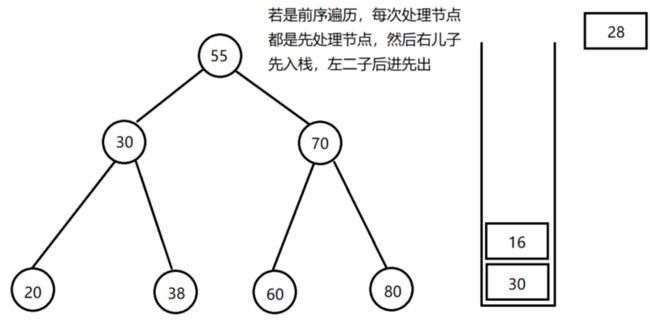
这里以前序遍历为例进行说明,利用 栈 的特点,从跟节点开始,先把根节点入栈,然后出栈的时候需要判断出栈元素是否为空,若不为空则需要先把 右儿子节点入栈,然后 左儿子 节点入栈,依此类推直到没有儿子节点的时候就可以继续 出栈 下一个元素了,直到 栈 元素为空表示遍历完毕,通过这种 压栈 的思想可以达到 遍历二分搜索树 的目的。
Tips:若不为空的节点没有儿子节点,这里实际处理它的儿子节点也会入栈
null。
2.3 实现原理图示
2.4 二分搜索树前序遍历压栈实现
下面展示的都是部分代码,需要结合之前的《数据结构-PHP 实现二分搜索树》,前序遍历操作就是把所有节点都访问一次,前序遍历 是先访问节点,再遍历左儿子树,然后再遍历右儿子树,要想达到这种效果,对于每个节点都是先处理当前节点,然后入栈右儿子,最后入栈左儿子,若出栈元素为空,打印 null 之后继续出栈:
Tips:若不为空的节点没有儿子节点,这里实际处理它的儿子节点也会入栈
null。
/**
* 前序遍历压栈实现
*/
public function preTraversalByStack() {
$stack = new StackByLinkedList();
//将根节点压入栈
$stack->push($this->root);
//循环依次出栈
$node = $stack->pop();
do {
if ($node != null) { //若出栈的当前节点不是空
echo $node->e . "
"; //先打印当前节点信息
//先入栈右儿子
$stack->push($node->right);
//然后入栈左儿子
$stack->push($node->left);
} else { //若是空
echo "null
";
}
//继续出栈
$node = $stack->pop();
} while (!$stack->isEmpty());
}下面是打印结果:
add(45);
$binarySearchTree->add(30);
$binarySearchTree->add(55);
$binarySearchTree->add(25);
$binarySearchTree->add(35);
$binarySearchTree->add(50);
$binarySearchTree->add(65);
$binarySearchTree->add(15);
$binarySearchTree->add(27);
$binarySearchTree->add(31);
$binarySearchTree->add(48);
$binarySearchTree->add(60);
$binarySearchTree->add(68);
//下面是预期想要的结果
/**
* 45
* /
* 30 55
* / /
* 25 35 50 65
* / / / /
* 15 27 31 48 60 68
*
*/
//调用前序遍历的递归实现
$binarySearchTree->preTraversalByStack();
/**
打印输出
45
30
25
15
null
null
27
null
null
35
31
null
null
null
*/Tips:可以看到打印输出结果和预期一致,并且和之前递归实现的方式一致,对于中序遍历、后续遍历来说具体实现逻辑比前序遍历要复杂一些。
代码仓库 :https://gitee.com/love-for-po...
扫码关注爱因诗贤
![]()