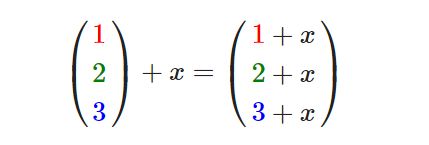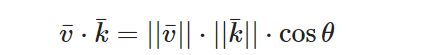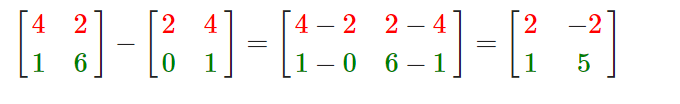Android OpenGL ES - GLSL基础篇

上节在绘制三角形的时候，简单讲解了一些着色器，GLSL 的相关概念，可能看的云里雾里的。不要担心，在本节中，我将详细讲解着色语言 GL Shader Language（GLSL）的一些基本的概念。

PS：
无特殊说明，文中的 GLSL 均指 OpenGL ES 2.0 的着色语言。

GLSL (GL Shader Language)

在上一节中，我们提到了GLSL 的语法与 C 语言很类似，也看到了一个非常简单的着色器，如下：
VertexShader

"attribute vec4 aPosition; \n"
     "void main() \n"
     "{ \n"
     "   gl_Position = aPosition; \n"
     "} \n";

Fragment Shader

 "precision mediump float;\n"
     "void main() \n"
     "{ \n"
     "   gl_FragColor = vec4 ( 1.0, 0.0, 0.0, 1.0 ); \n"
     "} \n";

和 C 语言程序对应，用 GLSL 写出的着色器，它同样包括：

• 变量 position
• 变量类型 vec4
• 限定符 attribute
• main 函数
• 基本赋值语句 gl_Position = aPosition
• 内置变量 gl_Position
• …

这一切，都是那么像C语言，所以，在掌握 C 语言的基础上，GLSL 的学习成本是很低的。

学习一门语言，我们无非是从变量类型，结构体，数组，语句，函数，限定符等方面展开。下面，我们就照着这个顺序，学习 GLSL。

变量

变量及变量类型

变量类型	描述	变量类别
void	用于无返回值的函数或空的参数列表
float, int, bool	浮点型，整型，布尔型的标量数据类型	标量
float, vec2, vec3, vec4	包含1，2，3，4个元素的浮点型向量	浮点型向量
int, ivec2, ivec3, ivec4	包含1，2，3，4个元素的整型向量	整型向量
bool, bvec2, bvec3, bvec4	包含1，2，3，4个元素的布尔型向量	布尔型向量
mat2, mat3, mat4	尺寸为2x2，3x3，4x4的浮点型矩阵	浮点矩阵
sampler2D, samplerCube	表示2D，立方体纹理的句柄	纹理句柄

除上述之外，着色器中还可以将它们构成数组或结构体，以实现更复杂的数据类型。

PS：

GLSL 中没有指针类型。

标量

标量(Scalar)只是一个数字（或者说是仅有一个分量的向量）,是只有大小没有方向的量
标量对应 C 语言的基础数据类型，它的构造和 C 语言一致，如下：

float mFloat = 1.0f;
bool mFlag = true;
mFloat = float(mFlag);     // bool -> float
mFlag = bool(mFloat);     // float -> bool

向量

向量最基本的定义就是一个方向。或者更正式的说，向量有一个方向(Direction)和大小(Magnitude，也叫做强度或长度)。
当构造向量时，向量构造器中的各参数将会被转换成相同的类型（浮点型、整型或布尔型）。往向量构造器中传递参数有两种形式：

• 如果向量构造器中只提供了一个标量参数，则向量中所有值都会设定为该标量值。
• 如果提供了多个标量值或提供了向量参数，则会从左至右使用提供的参数来给向量赋值，如果使用多个标量来赋值，则需要确保标量的个数要多于向量构造器中的个数。

向量构造器用法如下：

vec4 mVec4 = vec4(1.0);             // mVec4 = {1.0, 1.0, 1.0, 1.0}
vec3 mVec3 = vec3(1.0, 0.0, 0.5);  // mVec3 = {1.0, 0.0, 0.5}
vec3 tempVec3 = vec3(mVec3);             // tempVec3 = mVec3
vec2 mVec2 = vec2(mVec3);         // mVec2 = {mVec3.x, mVec3.y}

矩阵

单来说矩阵就是一个矩形的数字、符号或表达式数组。矩阵中每一项叫做矩阵的元素(Element)。下面是一个2×3矩阵的例子：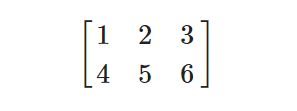

矩阵的构造方法则更加灵活，有以下规则：

• 如果对矩阵构造器只提供了一个标量参数，该值会作为矩阵的对角线上的值。例如 mat4(1.0) 可以构造一个 4 × 4 的单位矩阵
• 矩阵可以通过多个向量作为参数来构造，例如一个 mat2 可以通过两个 vec2 来构造
• 矩阵可以通过多个标量作为参数来构造，矩阵中每个值对应一个标量，按照从左到右的顺序

除此之外，矩阵的构造方法还可以更灵活，只要有足够的组件来初始化矩阵，其构造器参数可以是标量和向量的组合。在 OpenGL ES 中，矩阵的值会以列的顺序来存储。在构造矩阵时，构造器参数会按照列的顺序来填充矩阵，如下：

mat3 mMat3 = mat3(
 1.0, 0.0, 0.0,  // 第一列
 0.0, 1.0, 0.0,  // 第二列
 0.0, 1.0, 1.0); // 第三列

向量和矩阵的分量

单独获得向量中的组件有两种方法：即使用 "." 符号或使用数组下标方法。依据构成向量的组件个数，向量的组件可以通过 {x, y, z, w} ， {r, g, b, a} 或 {s, t, r, q} 等操作来获取。之所以采用这三种不同的命名方法，是因为向量常常会用来表示数学向量、颜色、纹理坐标等。其中的x、r、s 组件总是表示向量中的第一个元素，如下表：

分量访问符	符号描述
(x,y,z,w)	与位置相关的分量
(r,g,b,a)	与颜色相关的分量
(s,t,p,q)	与纹理坐标相关的分量

不同的命名约定是为了方便使用，所以哪怕是描述位置的向量，也是可以通过 {r, g, b, a} 来获取。但是在使用向量时不能混用不同的命名约定，即不能使用 .xgr 这样的方式，每次只能使用同一种命名约定。当使用 "." 操作符时，还可以对向量中的元素重新排序，如下：

vec3 mVec3 = vec3(0.0, 1.0, 2.0); // mVec3 = {0.0, 1.0, 2.0}
vec3 mTemp;
mTemp = mVec3.xyz; // mTemp = {0.0, 1.0, 2.0}
mTemp = mVec3.xxx; // mTemp = {0.0, 0.0, 0.0}
mTemp = mVec3.zyx; // mTemp = {2.0, 1.0, 0.0}

除了使用 "." 操作符之外，还可以使用数组下标操作。在使用数组下标操作时，元素 [0] 对应的是 x，元素 [1] 对应 y，以此类推。

向量和矩阵的运算

绝大多数情况下，向量和矩阵的计算是逐分量进行的（component-wise）。当运算符作用于向量或矩阵时，该运算独立地作用于向量或矩阵的每个分量。
以下是一些示例：

向量/矩阵与标量运算

标量(Scalar)只是一个数字（或者说是仅有一个分量的向量）。当把一个向量加/减/乘/除一个标量，我们可以简单的把向量的每个分量分别进行该运算。对于加法来说会像这样:

其中的+可以是+，-，·或÷，其中·是乘号。注意－和÷运算时不能颠倒（标量-/÷向量），因为颠倒的运算是没有定义的。

类似的
矩阵与标量之间的加减定义如下：

注意，数学上是没有向量/矩阵与标量相加这个运算的，但是很多线性代数的库都对它有支持,如GLM

向量之间的运算

向量加减

向量的加法可以被定义为是分量的(Component-wise)相加，即将一个向量中的每一个分量加上另一个向量的对应分量：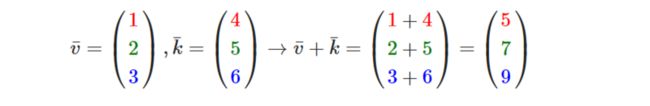

向量相乘

两个向量相乘是一种很奇怪的情况。普通的乘法在向量上是没有定义的，因为它在视觉上是没有意义的。但是在相乘的时候我们有两种特定情况可以选择：一个是点乘(Dot Product)，记作。

1. 点乘

两个向量的点乘等于它们的数乘结果乘以两个向量之间夹角的余弦值，两个向量的点击是一个标量。可能听起来有点费解，我们来看一下公式：

2.叉乘
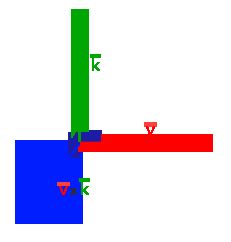
叉乘只在3D空间中有定义，它需要两个不平行向量作为输入，生成一个正交于两个输入向量的第三个向量。如果输入的两个向量也是正交的，那么叉乘之后将会产生3个互相正交的向量。接下来的教程中这会非常有用。下面的图片展示了3D空间中叉乘的样子：

矩阵之间的运算

矩阵与矩阵之间的加减就是两个矩阵对应元素的加减运算，所以总体的规则和与标量运算是差不多的，只不过在相同索引下的元素才能进行运算。这也就是说加法和减法只对同维度的矩阵才是有定义的。一个3×2矩阵和一个2×3矩阵（或一个3×3矩阵与4×4矩阵）是不能进行加减的。我们看看两个2×2矩阵是怎样相加的：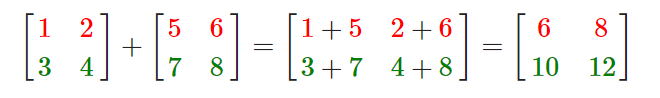

同样的法则也适用于减法：

1. 矩阵的数乘

和矩阵与标量的加减一样，矩阵与标量之间的乘法也是矩阵的每一个元素分别乘以该标量。下面的例子展示了乘法的过程：

现在我们也就能明白为什么这些单独的数字要叫做标量(Scalar)了。简单来说，标量就是用它的值缩放(Scale)矩阵的所有元素（译注：注意Scalar是由Scale + -ar演变过来的）。前面那个例子中，所有的元素都被放大了2倍。

到目前为止都还好，我们的例子都不复杂。不过矩阵与矩阵的乘法就不一样了。

1. 矩阵相乘

矩阵之间的乘法不见得有多复杂，但的确很难让人适应。矩阵乘法基本上意味着遵照规定好的法则进行相乘。当然，相乘还有一些限制：

1. 只有当左侧矩阵的列数与右侧矩阵的行数相等，两个矩阵才能相乘。
2. 矩阵相乘不遵守交换律(Commutative)，也就是说A⋅B≠B⋅AA⋅B≠B⋅A。

我们先看一个两个2×2矩阵相乘的例子：

现在你可能会在想了：天哪，刚刚到底发生了什么? 矩阵的乘法是一系列乘法和加法组合的结果，它使用到了左侧矩阵的行和右侧矩阵的列。我们可以看下面的图片：

结构体

与 C 语言相似，除了基本的数据类型之外，还可以将多个变量聚合到一个结构体中，下边的示例代码演示了在GLSL中如何声明结构体：

struct MyStruct
{
 vec4 color;
 vec2 position;
} myVertex;

首先，定义会产生一个新的类型叫做 MyStruct ，及一个名为 myVertex 的变量。结构体可以用构造器来初始化，在定义了新的结构体之后，还会定义一个与结构体类型名称相同的构造器。构造器与结构体中的数据类型必须一一对应，如下：

myVertex = MyStruct(vec4(0.0, 1.0, 0.0, 0.0), // color
 vec2(0.5, 0.5));           // position

结构体的构造器是基于类型的名称，以参数的形式来赋值。获取结构体内元素的方法和C语言中一致：

vec4 color = myVertex.color;
vec4 position = myVertex.position;

数组

除了结构体外，GLSL 中还支持数组。 语法与 C 语言相似，创建数组的方式如下代码所示：

float floatArray[4];
vec4 vecArray[2];

与C语言不同，在GLSL中，关于数组有两点需要注意：

• 除了 uniform 变量之外，数组的索引只允许使用常数整型表达式。
• 在 GLSL 中不能在创建的同时给数组初始化，即数组中的元素需要在定义数组之后逐个初始化，且数组不能使用 const 限定符。

函数

GLSL 函数的声明与 C 语言中很相似，无非就是返回值，函数名，参数列表。

GLSL 着色器同样是从 main 函数开始执行。另外， GLSL 也支持自定义函数。当然，如果一个函数在定以前被调用，则需要先声明其原型。

值得注意的一点是，GLSL 中函数不能够递归调用，且必须声明返回值类型（无返回值时声明为void）。如下：

vec4 getPosition(){ 
 vec4 v4 = vec4(0.0f,0.0f,0.0f,1.0f);
 return v4;
}

void doubleSize(inout float size){
 size= size*2.0  ;
}
//主函数
void main() {
 float psize= 10.0;
 doubleSize(psize);
 gl_Position = getPosition();
 gl_PointSize = psize;
}

限定符

存储限定符

在声明变量时，应根据需要使用存储限定符来修饰，类似 C 语言中的说明符。GLSL 中支持的存储限定符见下表：

限定符	描述
< none: default >	局部可读写变量，或者函数的参数
const	编译时常量，或只读的函数参数
attribute	由应用程序传输给顶点着色器的逐顶点的数据
uniform	在图元处理过程中其值保持不变，由应用程序传输给着色器
varying	由顶点着色器传输给片段着色器中的插值数据

• 本地变量和函数参数只能使用 const 限定符，函数返回值和结构体成员不能使用限定符。
• 数据不能从一个着色器程序传递给下一个阶段的着色器程序，这样会阻止同一个着色器程序在多个顶点或者片段中进行并行计算。
• 不包含任何限定符或者包含 const 限定符的全局变量可以包含初始化器，这种情况下这些变量会在 main() 函数开始之后第一行代码之前被初始化，这些初始化值必须是常量表达式。
• 没有任何限定符的全局变量如果没有在定义时初始化或者在程序中被初始化，则其值在进入 main() 函数之后是未定义的。
• uniform、attribute 和 varying 限定符修饰的变量不能在初始化时被赋值，这些变量的值由 OpenGL ES 计算提供。

默认限定符

如果一个全局变量没有指定限定符，则该变量与应用程序或者其他正在运行的处理单元没有任何联系。不管是全局变量还是本地变量，它们总是在自己的处理单元被分配内存，因此可以对它们执行读和写操作。

const 限定符

任意基础类型的变量都可以声明为常量。常量表示这些变量中的值在着色器中不会发生变化，声明常量只需要在声明时加上限定符 const 即可，声明时必须赋初值。

const float zero = 0.0;
const float pi = 3.14159;
const vec4 red = vec4(1.0, 0.0, 0.0, 1.0);
const mat4 identity = mat4(1.0);

• 常量声明过的值在代码中不能再改变，这一点和 C 语言或 C++ 一样。
• 结构体成员不能被声明为常量，但是结构体变量可以被声明为常量，并且需要在初始化时使用构造器初始化其值。
• 常量必须被初始化为一个常量表达式。数组或者包含数组的结构体不能被声明为常量（因为数组不能在定义时被初始化）。

attribute 限定符

GLSL 中另一种特殊的变量类型是 attribute 变量。attribute 变量只用于顶点着色器中，用来存储顶点着色器中每个顶点的输入（per-vertex inputs）。attribute 通常用来存储位置坐标、法向量、纹理坐标和颜色等。注意 attribute 是用来存储单个顶点的信息。如下是包含位置，色值 attribute 的顶点着色器示例：

attribute vec4 aPosition;
attribute vec4 aColor;
varying vec4 outColor;
void main(void) {
 outColor = aColor;
 gl_Position = aPosition;
}

着色器中的两个 attribute 变量 position 和 color 由应用程序加载数值。应用程序会创建一个顶点数组，其中包含了每个顶点的位置坐标和色值信息。可使用的最大 attribute 数量也是有上限的，可以使用 gl_MaxVertexAttribs 来获取，也可以使用内置函数 glGetIntegerv 来询问 GL_MAX_VERTEX_ATTRIBS。OpenGL ES 2.0 实现支持的最少 attribute 个数是8个。

关于由attribute修饰的变量到底是如何赋值的，我们前面也说过，这里呢也再重复一下

glLinkProgram(m_program_id);
//在OpenGL程序中获取对应属性名字在程序中的句柄
m_vertex_pos_handler = glGetAttribLocation(m_program_id, "aPosition");//这里的aPosition对应着上面的attribute vec4 aPosition;

// 使用glVertexAttribPointer方法
glVertexAttribPointer(m_vertex_pos_handler, 3, GL_FLOAT, GL_FALSE, 3 * sizeof(float), m_vertex_coors);

uniform 限定符

uniform 是 GLSL 中的一种变量类型限定符，用于存储应用程序通过 GLSL 传递给着色器的只读值。uniform 可以用来存储着色器需要的各种数据，如变换矩阵、光参数和颜色等。传递给着色器的在所有的顶点着色器和片段着色器中保持不变的的任何参数，基本上都应该通过 uniform 来存储。uniform 变量在全局区声明，以下是 uniform 的一些示例：

uniform mat4 viewProjMatrix;
uniform mat4 viewMatrix;
uniform vec3 lightPosition;

需要注意的一点是，顶点着色器和片段着色器共享了 uniform 变量的命名空间。对于连接于同一个着色程序对象的顶点和片段着色器，它们共用同一组 uniform 变量，因此，如果在顶点着色器和片段着色器中都声明了 uniform 变量，二者的声明必须一致。当应用程序通过 API 加载了 uniform 变量时，该变量的值在顶点和片段着色器中都能够获取到。

另一点需要注意的是，uniform 变量通常是存储在硬件中的”常量区”，这一区域是专门分配用来存储常量的，但是由于这一区域尺寸非常有限，因此着色程序中可以使用的 uniform 的个数也是有限的。可以通过读取内置变量 gl_MaxVertexUniformVectors 和 gl_MaxFragmentUniformVectors 来获得，也可以使用 glGetIntegerv 查询 GL_MAX_VERTEX_UNIFORM_VECTORS 或者 GL_MAX_FRAGMENT_UNIFORM_VECTORS 。OpenGL ES 2.0 的实现必须提供至少 128 个顶点 uniform 向量及 16 片段 uniform 向量。

关于由uniform修饰的变量到底是如何赋值的，我们使用

// C function GLint glGetUniformLocation ( GLuint program, const char *name )

varying 限定符

GLSL 中最后一个要说的存储限定符是 varying。varying 存储的是顶点着色器的输出，同时作为片段着色器的输入，通常顶点着色器都会把需要传递给片段着色器的数据存储在一个或多个 varying 变量中。这些变量在片段着色器中需要有相对应的声明且数据类型一致，然后在光栅化过程中进行插值计算。以下是一些 varying 变量的声明：

顶点着色器和片段着色器中都会有 varying 变量的声明，由于 varying 是顶点着色器的输出且是片段着色器的输入，所以两处声明必须一致。与 uniform 和 attribute 相同，varying 也有数量的限制，可以使用 gl_MaxVaryingVectors 获取或使用 glGetIntegerv 查询 GL_MAX_VARYING_VECTORS 来获取。OpenGL ES 2.0 实现中的 varying 变量最小支持数为 8。

回顾下最初那个着色器对应的 varying 声明：

// 顶点着色器
attribute vec4 aPosition;
attribute vec4 aColor;
varying vec4 outColor;
void main(void) {
 outColor = aColor;
 gl_Position = aPosition;
}

// 片段着色器
varying lowp vec4 outColor;
void main(void) {
 gl_FragColor = outColor;
}

参数限定符

GLSL 提供了一种特殊的限定符用来定义某个变量的值是否可以被函数修改，详见下表：

限定符	描述
in	默认使用的缺省限定符，指明参数传递的是值，并且函数不会修改传入的值（C 语言中值传递）
inout	指明参数传入的是引用，如果在函数中对参数的值进行了修改，当函数结束后参数的值也会修改（C 语言中引用传递）
out	参数的值不会传入函数，但是在函数内部修改其值，函数结束后其值会被修改

使用的方式如下边的代码：

vec4 myFunc(inout float myFloat, // inout parameter
 out vec4 myVec4,      // out parameter
 mat4 myMat4);          // in parameter (default)

精度限定符

OpenGL ES 与 OpenGL 之间的一个区别就是在 GLSL 中引入了精度限定符。精度限定符可使着色器的编写者明确定义着色器变量计算时使用的精度，变量可以选择被声明为低、中或高精度。精度限定符可告知编译器使其在计算时缩小变量潜在的精度变化范围，当使用低精度时，OpenGL ES 的实现可以更快速和低功耗地运行着色器，效率的提高来自于精度的舍弃，如果精度选择不合理，着色器运行的结果会很失真。

OpenGL ES 对各硬件并未强制要求多种精度的支持。其实现可以使用高精度完成所有的计算并且忽略掉精度限定符，然而某些情况下使用低精度的实现会更有优势，精度限定符可以指定整型或浮点型变量的精度，如 lowp，mediump，及 highp，如下：

限定符	描述
highp	满足顶点着色语言的最低要求。对片段着色语言是可选项
mediump	满足片段着色语言的最低要求，其对于范围和精度的要求必须不低于lowp并且不高于highp
lowp	范围和精度可低于mediump，但仍可以表示所有颜色通道的所有颜色值

具体用法参考以下示例：

highp vec4 position;
varying lowp vec4 color;
mediump float specularExp;

除了精度限定符，还可以指定默认使用的精度。如果某个变量没有使用精度限定符指定使用何种精度，则会使用该变量类型的默认精度。默认精度限定符放在着色器代码起始位置，以下是一些用例：

precision highp float;
precision mediump int;

当为 float 指定默认精度时，所有基于浮点型的变量都会以此作为默认精度，与此类似，为 int 指定默认精度时，所有的基于整型的变量都会以此作为默认精度。在顶点着色器中，如果没有指定默认精度，则 int 和 float 都使用 highp，即顶点着色器中，未使用精度限定符指明精度的变量都默认使用最高精度。在片段着色器中，float 并没有默认的精度设置，即片段着色器中必须为 float 默认精度或者为每一个 float 变量指明精度。

此时我们应该也能理解我们一直以来的片段着色器的意思了

 "precision mediump float; \n"//定义float的默认精度，否则片段着色器会报错
     "void main() \n"
     "{ \n"
     "   gl_FragColor = vec4 ( 1.0, 0.0, 0.0, 1.0 ); \n"
     "} \n";

小结

本章介绍了关于GLSL的一些基础语法语句之类的知识，总的来说GLSL基本还是与C语言有很多相似之处的，如果有C语言的基础的话，学习GLSL的语法并不难。

参考资料

GLSL2.0官方参考文档