local minimum or global minimum
local minimum or global minimum ,in machine leaning it is a question to discuss
在数学中,极大值与极小值(又被称为极值)是指在一个域上函数取得最大值(或最小值)的点的函数值。而使函数取得极值的点(的横坐标)被称作极值点。这个域既可以是一个邻域,又可以是整个函数域(这时极值称为最值)。
局部最大值:如果存在一个 ε > 0,使的所有满足|x-x*| < ε 的x都有f(x*) ≥ f(x) 我们就把点x*称为一个函数 f 的局部最大值。从函数图像上看,局部最大值就像是山顶。
局部最小值: 如果存在一个 ε > 0,使的所有满足|x-x*| < ε 的x都有f(x*) ≤ f(x) 我们就把点x*称为一个函数 f 的局部最小值。从函数图像上看,局部最小值就像是山谷的底部。
全局(或称'绝对')最大值 如果点x* 对于任何x都满足f(x*) ≥ f(x),则点点x*称为全局最大值。同样如果如果点x* 对于任何x都满足f(x*) ≤ f(x),则点点x*称为全局最小值。全局最值一定是局部极值,反之则不然。
极值的概念不仅仅限于定义在实数域上的函数。定义在任何集合上的实数值函数都可以讨论其最大最小值。为了定义局部极值,函数值必须为实数,同时此函数的定义域上必须能够定义邻域。邻域的概念使得在x的定义域上可以有|x - x*| < ε.
局部最大值(最小值)也被称为极值(或局部最优值),全局最大值(最小值)也被称为最值(或全局最优值).
machine learning 中的梯度下降就是求用来局部极值的方法:
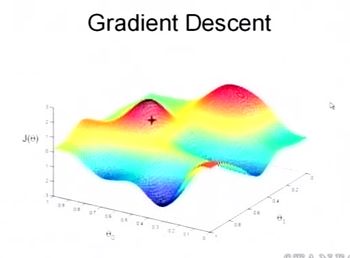
梯度下降定义:就是利用负梯度方向来决定每次迭代的新的搜索方向,使得每次迭代能使待优化的目标函数逐步减小。梯度下降法是2范数下的最速下降法。
最速下降法的一种简单形式是:x(k+1)=x(k)-a*g(k),其中a称为学习速率,可以是较小的常数。g(k)是x(k)的梯度。 上面的图是描述梯度下降的一幅图,第一步是给k给一个初值,假设随机给的初值是在图上的十字点。然后我们将k按照梯度下降的方向进行调整,就会使得g(k)往更低的方向进行变化,如图所示,算法的结束将是在K下降到无法继续下降为止。(也就是算法收敛的地方)这个算法将会在很大的程度上被初始点的选择影响而陷入局部最小点 。
直观的说,就是在一个有中心的等值线中,从初始值开始,每次沿着垂直等值线方向移动一个小的距离,最终收敛在中心。
对于某一个性能指数,我们能够运用梯度下降法,使这个指数降到最小。若该指数为均方误差,我们便得到了最小均方误差(LMS)算法。
先保存下来吧!