H5游戏开发之多边形碰撞检测

2D多边形碰撞检测
介绍
这是一篇论证如何在2D动作游戏中执行碰撞检测的文章（Mario,宇宙入侵者等），为了保证它的高效性和精确性，碰撞检测是以多边形为基础的，而不是以sprite为基础。这是两种不同的设计途径。
基于sprite的检测执行的是检测sprites的像素的交叉，以这种方式来检测碰撞。多边形是使用向量数学来精确的计算点，时间和碰撞的方向。当多边形只是一种近似sprite自身的时候，它就超越了sprite系统。
表现出了更精确的物理现象，例如弹性，摩擦，在一个随机的形状中来处理斜坡。
碰撞检测相对一个高速的sprite来讲是更加的精确的。在一个基于sprite的系统中，对象有可以在一个强力的跳跃中因为速度太快而相互穿越。
这是一个基于向量数学的系统，所以可以扩展到3D，但是一个sprite碰撞系统被完全的限制到了2D中。
特色：
因为运算法则的限制，系统只能操作凸多边形，例如三角形，矩形，五边形，圆形。在一个非凸多边形中，你可以将这些多边形分成三角形来处理。
无论是快速或者慢速的多边形，他的处理方式都是一样的。不管对象的移动有多快，碰撞也不会丢失的。他也可以来处理交叠，分开已经交叉的对象。
里面的范例也有线段的交叉。这可以用来模拟子弹。
它也提供了一些简单的物理系统，模拟弹力，一些基本的摩擦力和静摩擦力。在斜坡上的一些特性它也可以模拟。
这里也有一个刚体系统的例子，引用的是Chrsi Hecker的物理文章。
局限性：
碰撞的种类，我的意思是它不能顺序的处理碰撞。在一个快速的对象中这可能会有问题。一旦一个碰撞被检测了，它便会直线的离开。你可以检测到第一个碰撞并处理它，然后再找到其他的碰撞。但是在一个2D的动作游戏中，这是很具有杀伤力的。
必要条件：
一些普通的原料，一个编译器，范例是基于GLUT（GL开发包）的框架，所以需要下载一个小的GLUT SDK和一个兼容opengl的显卡。
你还需要对向量数学有一个基本的了解。这里的文章不准备对点乘进行讲解，但是它可以帮助你对向量的操作有更好的了解。
对于刚体，你需要对Chris Hecker的文章仔细的阅读一下。它需要你付出更多，但是它是值得的，并不是多么的困难。
内容列表：
1：分离轴的方法
2：扩展应用于碰撞反馈的分离轴的方法。
分离轴的方法：
这是碰撞检测的核心，原理是非常简单的，也非常的容易实现。它也是快速和稳定的，因为没有除法在运算中被使用。我将会带给大家一个简单的两个BOX碰撞测试的例子。

 

 

 

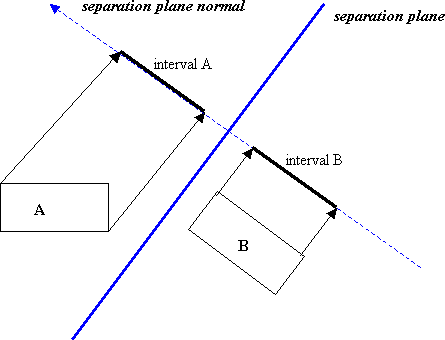
该运算法则试着来确定两个对象中的一个合适的面。如果有这样的一个面存在，如果有这样的面存在，说明对象是分离的，没有交叉。
为了确定对象是否是分离的。只要将这个对象投影到这个平面的法线上，然后比较它们之间的间隔看他们是否交叉。
所以，很明显有无数个边能够适合这两个分离的对象，但是已经证明你只要测试少数的几个面就可以了，对于上面图形中的两个BOX，你可以看到边的法线是形状B的边。
从上面的这些形状中可以发现，那些即将被测试的分离面是两个BOX的边的法线。对于这两个BOX而言，你只需要测试4个分离的面。在这4个面中，一旦你发现一个分离面分隔了这两个BOX。你就可以知道了这两个BOX是分离的。然后返回一个没有碰撞的标记。
如果这4个面没有分隔这两个BOX，那么这两个BOX肯定是交叉的，说明他们有一个碰撞。
扩展到一般的多边形，该运算法则仍然是适用的。只不过是测试的边变化了。那些分离的面的法线是和每个多边形的边的垂直方向是平行的。在下面的图形中，你可以看到有两个分离面被测试。在红色的面被测试的时候，你可以看到那两个间隔是交叉的，但是在蓝色的被测试的时候，间隔并没有交叉。所有蓝色的面是分离面，对象因此是没有交叉的。

 

 

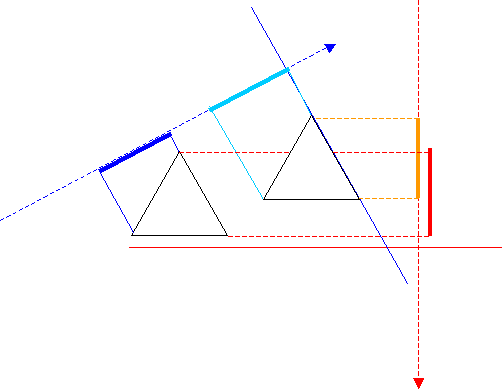
现在，我们有一个算法来检测两个多边形是否是相交的。代码可以分为三个部分：

a)         生成需要测试的分离轴

b)        计算每一个多边形在分离轴法线上的投影

c)        检测这些投影是否相交

bool Intersect(Polygon A, Polygon B) {      for(I = 0; I < A.num_edges; I ++)      {            Vector N = Vector(-A.EdgeDir[I].y, A.EdgeDir[I].x);            if (AxisSeparatePolygons(N, A, B))                  return false;       }        for(I = 0; I < B.num_edges; I ++)        {              Vector N = Vector(-B.EdgeDir[i].y, B.EdgeDir[I].x);              if (AxisSeparatePolygons (N, A, B))                    return false;        }        return true;  }

 

void CalculateInterval(Vector Axis, Polygon P, float& min, float& max)  {        float d = Axis dot P.vertex[0];        min = max = d;        for(I = 0; I < P.num_vertices; I ++)        {              float d = P.vertex[I] dot Axis;              if (d < min)                    min = d;              else                    if(d > max)                          max = d;        }  }

到这里，这个计算两个2D多边形碰撞的运算法则是非常快和稳定的。边的方向不一定是单位化的，所以你可以避免将边的方向都存储起来，你可以直接根据多边形的顶点来构建这些边的方向。

for(J = A.num_vertices-1, I = 0; I < A.num_vertices; J = I, I ++)  {        Vector E = A.vertex[I] – A.vertex[J];        Vector N = Vector(-E.y, E.x);        if (AxisSeparatePolygons(N, A, B))              return false;  }

扩展用于碰撞反馈的分离轴的方法：
检测多边形是否碰撞是非常有用处的，但是我们可以做的更多。当多边形交叉后，我希望能够让多边形分离来制止他们交叉。
分隔轴的方法还是要被用到的，通过作一个细微的额外工作。他能够返回他穿刺的深度和方向，并以此来分离它们。一个交叉的深度和方向的结合体也被称为MTD，或者是最小的转换距离。这个最小的向量需要让对象分离来制止他们交叉。
我们可以借助于分离轴来计算MTD。
当对象交叉的时候，我们知道了两个对象的交叉的每个分离轴的间隔距离。沿着这个轴的两个间隔的交叉的量提供了一个推进向量，你需要将其应用于这两个对象来让这些对象的投影来制止他们在这个轴上的交叉。

 

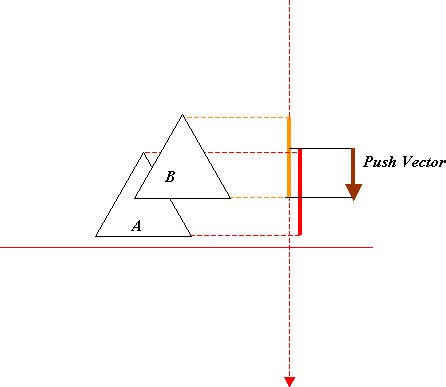
"推力向量"是一个向量，它的作用是你需要应用到A中以便制止他同B交叉。
很明显，你不能让这个对象沿着一个随机的轴来分离。待选的这些轴中应该选择那个交叉的间隔最小的轴。这个推力向量提供了一个最小的转换的距离。

bool Intersect(Polygon A, Polygon B, Vector& MTD)  {         // potential separation axes. they get converted into push         vectors Vector Axis[32];         // max of 16 vertices per polygon         int iNumAxis = 0;         for(J = A.num_vertices–1, I = 0; I < A. num_vertices; J = I, I ++)         {                Vector E = A.vertex[I] – A.vertex[J];                Axis[iNumAxis++] = Vector(-E.y, E.x);                 if (AxisSeparatePolygons(N, A, B))                       return false;         }         for(J = B. num_vertices–1, I = 0; I < B.num_vertices; J = I, I ++)         {                Vector E = B.vertex[I] – B.vertex[J];                Axis[iNumAxis++] = Vector(-E.y, E.x);                        if (AxisSeparatePolygons (N, A, B))                       return false;         }                 // find the MTD among all the separation vectors         MTD = FindMTD(Axis, iNumAxis);         // makes sure the push vector is pushing A away from B         Vector D = A.Position – B.Position;         if (D dot MTD < 0.0f)                MTD = -MTD;         return true;  }

 

bool AxisSeparatePolygons(Vector& Axis, Polygon A, Polygon B)  {         float mina, maxa;         float minb, maxb;         CalculateInterval(Axis, A, mina, maxa);         CalculateInterval(Axis, B, minb, maxb);         if (mina > maxb || minb > maxa)                return true;         // find the interval overlap         float d0 = maxa - minb;         float d1 = maxb - mina;         float depth = (d0 < d1)? d0 : d1;         // convert the separation axis into a push vector (re-normalise         // the axis and multiply by interval overlap)         float axis_length_squared = Axis dot Axis;         Axis *= depth / axis_length_squared;         return false;  }

 

Vector FindMTD(Vector* PushVectors, int iNumVectors)  {         Vector MTD = PushVector[0];         float mind2 = PushVector[0] dot PushVector[0];         for(int I = 1; I < iNumVectors; I ++)         {                float d2 = PushVector[I] * PushVector[I];                if (d2 < mind2)                {                       mind2 = d2;                       MTD = PushVector[I];                }         }         return MTD;  }

当对象交叉的情况下，你知道了MTD向量，分离他们就简单了。

A.Postion += MTD * 0.5f; B.Position -= MTD * 0.5f;

 

 

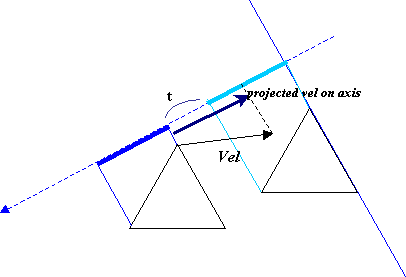
这只不过是一个投影数学。如果间隔是分离的，我们就需要计算一下这两个间隔接触的时间。
比较一下那个"静态"的分离轴的计算方法，有一个额外的轴我们需要测试，这很明显是一个相对于位移向量（速度向量）的轴。
所以对于每个分离轴，有三种选择。
间隔重叠
间隔分离，但是在未来的某个时间会重叠。
间隔分离，但是在未来的某个时间不会重叠或者是碰撞的很晚。
第3个选项的意思是对象不会在这帧上碰撞，分离轴真正的分离里这些对象。在这两个对象之间在这一帧上没有任何的碰撞。
AxisSeparatePolygon()函数返回交叠的量或者碰撞的时间，为了区分这两种情况，当一个交叠被发现的时候，一个负数被返回，如果在将来一个碰撞被检测到了，一个整数被返回的，函数类似下列的函数：

bool AxisSeparatePolygons(Vector Axis, Polygon A, Polygon B, Vector Offset, Vector Vel, float& t, float tmax);

Offset是A和B的相对的位置，Vel是A和B的相对的速度。
当找到碰撞面的时候，对于MTD是非常容易被找到的，但是对于在未来的某个时间的碰撞则优先于交叉的，如果碰撞在未来的某个时间被发现，最近一个会被选择。
如果什么都没有发现，我只处理交叉，象以前那样，最小的交叠会被使用。
碰撞计算的函数然后返回碰撞的法线，碰撞的深度（一个负数）或者碰撞的时间（一个正数）。
最终的伪代码如下：

bool Collide(     const Vector* A, int Anum,                              const Vector* B, int Bnum,                              const Vector& xOffset, const Vector& xVel,                              Vector& N, float& t)  {         if (!A || !B) return false;                      // All the separation axes         // note : a maximum of 32 vertices per poly is supported         Vector xAxis[64];         float taxis[64];         int iNumAxes=0;         xAxis[iNumAxes] = Vector(-xVel.y, xVel.x);         float fVel2 = xVel * xVel;         if (fVel2 > 0.00001f)         {                if (!IntervalIntersect( A, Anum, B, Bnum, xAxis[iNumAxes], xOffset, xVel, taxis[iNumAxes], t))                        return false;                iNumAxes++;         }         // test separation axes of A         for(int j = Anum-1, i = 0; i < Anum; j = i, i ++)         {                Vector E0 = A[j];                Vector E1 = A[i];                Vector E = E1 - E0;                xAxis[iNumAxes] = Vector(-E.y, E.x);                               if (!IntervalIntersect( A, Anum, B, Bnum, xAxis[iNumAxes], xOffset, xVel, taxis[iNumAxes], t))                       return false;               iNumAxes++;         }         // test separation axes of B         for(int j = Bnum-1, i = 0; i < Bnum; j = i, i ++)         {                Vector E0 = B[j];                Vector E1 = B[i];                Vector E = E1 - E0;                xAxis[iNumAxes] = Vector(-E.y, E.x);                if (!IntervalIntersect( A, Anum, B, Bnum, xAxis[iNumAxes], xOffset, xVel, taxis[iNumAxes], t))                       return false;               iNumAxes++;        }                if (!FindMTD(xAxis, taxis, iNumAxes, N, t))                return false;         // make sure the polygons gets pushed away from each other.         if (N * xOffset < 0.0f)                N = -N;         return true;  }

 

bool AxisSeparatePolygons ( Vector N, Polygon A, Polygon B, Vector Offset, Vector Vel, float &t, float tmax)  {         float min0, max0;         float min1, max1;         CalculateInterval(N, A, min0, max0);         CalculateInterval(N, B, min1, max1);                 float h = Offset dot N;         min0 += h;         max0 += h;         float d0 = min0 - max1; // if overlapped, do < 0         float d1 = min1 - max0; // if overlapped, d1 > 0         // separated, test dynamic intervals         if (d0 > 0.0f || d1 > 0.0f)         {                float v = Vel dot N;                // small velocity, so only the overlap test will be relevant.                if (fabs(v) < 0.0000001f)                       return false;                float t0 =-d0 / v; // time of impact to d0 reaches 0                float t1 = d1 / v; // time of impact to d0 reaches 1                // sort the times.                if (t0 > t1)                {                       float temp = t0;                       t0 = t1;                       t1 = temp;                }                // take the minimum positive                taxis = (t0 > 0.0f)? t0 : t1;                // intersection time too late or back in time, no collision                if (taxis < 0.0f || taxis > tmax)                       return true;                return false;         }         else         {                // overlap. get the interval, as a the smallest of |d0| and |d1|                // return negative number to mark it as an overlap                taxis = (d0 > d1)? d0 : d1;                return false;         }  }

 

bool FindCollisionPlane (Vector* Axis, float* taxis, int iNumAxes, Vector& Ncoll, float& tcoll)  {         // find collision first         int mini = -1;         tcoll = 0.0f;         for(int i = 0; i < iNumAxes; i ++)         {                if (taxis[i] > 0.0f)                {                       if (taxis[i] > tcoll)                       {                              mini = i;                              tcoll = taxis[i];                              Ncoll = Axis[i];                              Ncoll.Normalise(); // normalise axis                       }               }        }        // found a collision         if (mini != -1)                return true;         // nope, find overlaps         mini = -1;         for(int i = 0; i < iNumAxes; i ++)         {                float n = Axis[i].Normalise(); // axis length                taxis[i] /= n; // normalise interval overlap too                // remember, those numbers are negative, so take the closest to 0                if (mini == -1 || taxis[i] > tcoll)                {                       mini = i;                       tcoll = taxis[i];                       Ncoll = Axis[i];                }         }                 return (mini != -1);  }

这就是全部了，一个检测多边形的碰撞的系统返回一个未来的时间或者是当交叉的时候返回那个碰撞的面。