精读：用three.js实现全景图

之前做组内分享，选了threejs来学习一下，接下来就把用threejs实现的全景图来解读一下。

1. three.js基础回顾

1.1 three.js概览

1. 是什么？
Three.js 是一款 webGL 框架，它封装了底层的图形接口，使得能够在无需掌握繁冗的图形学知识的情况下，也能用简单的代码实现三维场景的渲染。

2. 核心

• 渲染器: 将场景中的物体进行渲染
• 场景: 场景是所有物体的容器，也对应着我们创建的三维世界
• 相机: 一种投影方式，将三维的场景显示到二维的屏幕上

1.2 相机

1. 是什么
我们使用Three.js创建的场景是三维的，而通常情况下显示屏是二维的，那么三维的场景如何显示到二维的显示屏上呢？照相机就是这样一个抽象，它定义了三维空间到二维屏幕的投影方式，用“照相机”这样一个类比，可以使我们直观地理解这一投影方式。

2. 分类

• 正交投影照相机: 对于在三维空间内平行的线，投影到二维空间中也一定是平行的
• 透视投影照相机: 有近大远小的效果

1.3 模型

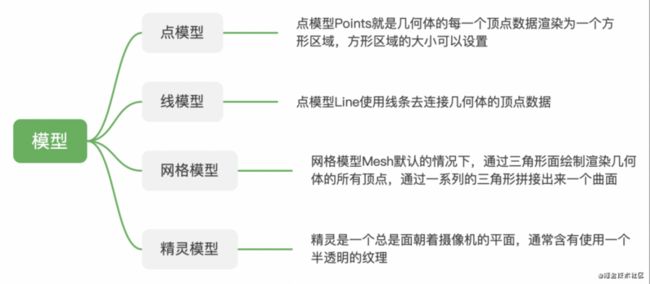
1. 主要有以下几种模型

2. 模型包括什么

• 几何形状
• 材质

1.4 光与影

1. 分类

• 环境光

指场景整体的光照效果。是由于场景内若干光源的多次反射形成的亮度一致的效果，通常用来为整个场景指定一个基础亮度

• 点光源

点光源是不计光源大小，可以看作一个点发出的光源。点光源照到不同物体表面的亮度是线性递减的

• 平行光

对于任意平行的平面，平行光照射的亮度都是相同的

• 聚光灯

聚光灯是一种特殊的点光源，它能够朝着一个方向投射光线

• 阴影

明暗是相对的，阴影的形成也就是因为比周围获得的光照更少。因此，要形成阴影，光源必不可少。

2. 全景图的实现

• 建立球体模型并令照相机位于球体中
• 不断移动照相机的位置使其观察到球体内的各个角度

2.1 建立基本场景

• 初始化渲染器

const setupRenderer = () => {
  const renderer = new THREE.WebGLRenderer({antialias: true})
  renderer.setSize(window.innerWidth, window.innerHeight)
  document.body.appendChild(renderer.domElement)
  return renderer
}

• 初始化相机

// 建立透视投影相机制造出“近大远小”的效果
const setupCamera = () => {
  const aspectRatio = window.innerWidth / window.innerHeight
  const camera = new THREE.PerspectiveCamera(90, aspectRatio, 0.0001, 10000)
  camera.position.set(window.obj.camerax, window.obj.cameray, window.obj.cameraz)

  return camera
}

• 初始化场景scene和辅助线

  const scene = new THREE.Scene()
  const axesHelper = new THREE.AxesHelper(1000)
  const cameraHelper = new THREE.CameraHelper(camera)
  const gridHelper = new THREE.GridHelper(1000, 10)

  // 布置场景
  scene.add(axesHelper)
  scene.add(cameraHelper)
  scene.add(gridHelper)

• 建立球体模型

// 采用加载纹理贴图的方式将一张普通的全景图贴在球体的表面
const sphereGeo = new THREE.SphereGeometry(radius)
const sphereMaterial = new THREE.MeshBasicMaterial({
    map: texture,
    side: THREE.DoubleSide,
})
const sphere = new THREE.Mesh(sphereGeo, sphereMaterial)

这样，基本的场景就展现出来了。此时我们只能看到球中的一个方向。

我们想要的效果是当滑动鼠标时，可以看到球中不同方向的场景。

2.2 核心：鼠标移动-相机移动

1. 涉及到以下几点：

• 监听鼠标的按下、移动事件
• 鼠标移动距离转化成经纬度
• 经纬度转化成相机的坐标

2. 代码解读

• 监听鼠标事件

// mousedown事件，记录移动的起点
window.addEventListener('mousedown', e => {
    startPosX = e.clientX
    startPosY = e.clientY
    startTs = Date.now()
    isMouseDown = true
  })
// mousemove, 记录移动的终点，并调用move函数进行实时计算
window.addEventListener('mousemove', e => {
    if (!isMouseDown) return
    const posX = e.clientX
    const posY = e.clientY
    const curTs = Date.now()

    // 根据起始和移动过程中的坐标、移动的时间来移动相机
    let startPos = { x: startPosX, y: startPosY };
    let endPos = { x: posX, y: posY };
    let duration = curTs - startTs;
    
    move(startPos, endPos, duration)

    // 以当前的终点为下一次的起点
    startPosX = posX
    startPosY = posY
    startTs = curTs
})

• move函数的实现：根据转化出来的相机坐标实时的设置相机的位置

  • 鼠标移动距离->经纬度
  • 经纬度-坐标

const move = (startPos, endPos, duration) => {
    if (duration === 0) return

    const { x: sx, y: sy } = startPos
    const { x: ex, y: ey } = endPos
    const vx = (ex - sx) / duration// X 轴方向上的速度
    const vy = (ey - sy) / duration// Y 轴方向上的速度
    // 1.鼠标移动距离->经纬度
    const { longtitude, latitude } = getMovPos({
        startPos,
        endPos: { x: vx * moveBuffTime + ex, y: vy * moveBuffTime + ey },
        curRotate: { longtitude: movObj.longtitude , latitude: movObj.latitude },
    })
   
   // 设置移动参数
    // 在update中设置相机实时的坐标会使移动过程更细腻
    const gsapOpts = {
      ease: "power4.out",
      duration: 1,
      onUpdate: () => {
           // 2.经纬度->相机的坐标
        const { latitude: newLati, posObj: newPos } = setCameraPos({
          longtitude: movObj.longtitude,
          latitude: movObj.latitude
        });

        movObj.latitude = newLati;
        movObj.longtitude = longtitude;

        // 3. 设置摄像机坐标
        posObj.camerax = newPos.x;
        posObj.cameray = newPos.y;
        posObj.cameraz = newPos.z;
      },
      
    };
    gsap.to(movObj, gsapOpts);
  }

在这里，用了gsap的动画来实现移动的动画，并且在动画更新过程中实时的计算。

之前在修改的过程中，有采用过如下写法，即对于相机坐标的计算、动画移动是顺序执行的，没有在update函数中实时的进行计算。这样会导致实际看到的效果是：当我们只横向移动鼠标时（改变精读），场景也会在竖直方向上有变化（纬度也变）

const { latitude: newLatitude, posObj: newPos } = setCameraPos({longtitude: movObj.longtitude, latitude: movObj.latitude})
// 3.移动相机
gsap.to(posObj, {
    ease: 'power4.out',
    duration: 1,
    camerax: newPos.x,
    cameray: newPos.y,
    cameraz: newPos.z,
})
movObj.longtitude = longtitude
movObj.latitude = latitude

• 鼠标移动距离->经纬度

我理解的0.138和0.12这两个比例值都可以变化，完全取决于你想让鼠标移动多少代表经度和维度的一圈而已。

这样每次在当前经度/纬度的基础上，再加上鼠标移动距离对应的一段增量(如： (sx - ex) * 0.138)就得到了新的经/纬度

const { x: sx, y: sy } = startPos
  const { x: ex, y: ey } = endPos
  const { longtitude: curLongtitude, latitude: curLatitude } = curRotate

  const longtitude = (sx - ex) * 0.138 + curLongtitude
  const latitude = (sy - ey) * 0.12 + curLatitude
  return {
    longtitude,
    latitude,
}

• 经纬度->坐标

  • 角度->弧度：三角函数计算用到的是弧度
  • 涉及到了数学上的计算：已知球体的半径，计算空间中的某一点的坐标

function setCameraPos ({latitude,longtitude}) {
    const newLatitude = Math.max(-85, Math.min(85, latitude))
    //将经纬度转化为弧度
    const phi = THREE.MathUtils.degToRad(newLatitude)
    const theta = THREE.MathUtils.degToRad(longtitude)
    const posObj = {
        x: 0,
        y: 0,
        z: 0,
    }
    // 关键公式计算
    const r = 100;
    posObj.y = r * Math.sin(phi);
    const ob = r * Math.cos(phi);
    posObj.z = ob * Math.cos(theta);
    posObj.x = ob * Math.sin(theta);
    
    return {
        latitude: newLatitude,
        posObj,
    }
}

对于空间中某一点坐标的计算，我们可以看下以下这张图

对于空间中的某一点D，已知OD是半径，∠AOB就是经度，∠DOB就是纬度

那么D在y轴上的距离就是OE=DB=OD * sin(∠DOB)
OB = OD * cos(∠DOB)
D在x轴上的距离就是OC=AB=OB * sin(∠AOB)
D在Z轴上的距离就是Oa=OB *cos(∠AOB)

所以根据以上公式就能将经纬度转化为坐标，即上述代码中的计算。

至此，已基本完成了全景图的效果。

点击获取完整代码