Hash碰撞与拒绝服务攻击
文/玄魂
1.Hash与Hash碰撞
Hash,简单来讲,是一种将任意长度的输入变换成固定长度的输出,固定长度的输出在“实际应用场景”下可以代表该输入。Hash函数通常被翻译成散列函数。Hash通常用来校验信息的一致性。
Hash函数的实现多种多样,在安全领域应用最为广泛的是SHA-x系列和MDx系列。Hash函数也划分为带密钥的Hash函数和不带密钥的Hash函数,通常所说的Hash函数是不带密钥的Hash函数。这里对Hash算法的实现原理不做更多的探讨。
| 篇外补充: Hash函数的定义和性质 |
由于Hash固定长度输出的特性,必然会存在多个不同输入产生相同输出的情况。如果两个输入串的hash函数的值一样,则称这两个串是一个碰撞(Collision)。在理论范围内,存在一个输出串对应无穷多个输入串,所以碰撞具有其必然性。
如果找到碰撞,那么意味着我们可以破坏信息的一致性而不被接收方察觉,搜寻指定输入的Hash碰撞值的过程被称作“Hash破解”。这里需要说明的是,Hash函数必须是不可逆的,所以不存在从散列值到原始输入的破解(这里不包括暴力破解,使用彩虹表是暴力破解的最佳方式,但是仍然无法保证破解到的数据是原始数据)。设计不良的Hash算法,很容易让人找到碰撞值,例如(参考网址:http://www.laruence.com/2011/12/30/2435.html):
“
在PHP中,如果键值是数字, 那么Hash的时候输入值就是数字本身, 一般的时候都是, index & tableMask. 而tableMask是用来保证数字索引不会超出数组可容纳的元素个数值, 也就是数组个数-1.
PHP的Hashtable的大小都是2的指数, 比如如果你存入10个元素的数组, 那么数组实际大小是16, 如果存入20个, 则实际大小为32, 而63个话, 实际大小为64. 当你的存入的元素个数大于了数组目前的最多元素个数的时候, PHP会对这个数组进行扩容, 并且从新Hash.
现在, 我们假设要存入64个元素(中间可能会经过扩容, 但是我们只需要知道, 最后的数组大小是64, 并且对应的tableMask为63:0111111), 那么如果第一次我们存入的元素的键值为0, 则hash后的值为0, 第二次我们存入64, hash(1000000 & 0111111)的值也为0, 第三次我们用128, 第四次用192…
”
一个“优良”的hash函数 f 应当满足以下三个条件:
- 任意y,找x,使得f(x)=y,非常困难。
- 给定x1,找x2,使得f(x1)=f(x2),非常困难。
- 找x1,x2,使得f(x1)=f(x2),非常困难。
上面的“非常困难”的意思是除了枚举外不可能有别的更快的方法。几乎所有的寻找碰撞的方法都从第三条入手,即找到两个不一样的输入得到相同的输出。
寻找Hash碰撞的方法也很多如用于一般性攻击的生日攻击和模差分法,用于攻击具有分组链结构的Hash方案的中间相遇攻击,于攻击基于模算术的Hash函数的修正分组攻击。这里我简要介绍以下四种寻找碰撞的方法:
- 相等子串法
- 生日攻击法
- 中间相遇法
- 模差分法
“相等子串法”是针对某些Hash函数具有相同的字符串组合在上下文中相同位置的Hash值都相同的特性来构造碰撞的。比如f(“string1”)=f(“string2”),那么字符串“aaastring1bbb”与字符串“aaastring2bbb”中,“string1”与“string2”具有相同的Hash值。针对这个特性我们可以构造任意多的碰撞,比如“Ly”和“nz”的Hash值相同,那么“LyLy”、“nznz”、“Lynz”、“nzLy”的Hash值都相同。
| 设h:X->Y是一个Hash函数,X和Y都是有限的,并且|X|>=2|Y|,记|X|=m,|Y|=n。显然至少有n个碰撞,问题是如何去找到这些碰撞。一个很自然的方法是随机选择k个不同的元素x1,x2,x3,••••••,xk ∈X,计算yI=h(xi),1<=i<=k,然后确定是否有一个碰撞发生。这个过程类似于把k个球随机地扔到n个箱子里边,然后检查看是否某一箱子里边至少有两个球。k个球对应于k个随机数x1,x2,x3,••••••,xk,n个箱子对应于Y中的n个可能的元素。我们将计算用这种方法找到一个碰撞的概率的下界,该下界只依赖于k和n,而不依赖于m。 |
| 因为我们关心的是碰撞概率的下界,所以可以假定对所有y∈Y,有|h-1(y)|≈m/n。这个假定是合理的,这是因为如果原像集h-1(y)( y∈Y)不是近似相等的,那么找到一个碰撞的概率将增大。 |
| 因为原像集h-1(y)( y∈Y)的个数都近似相等,并且xI(1<=i<=k)是随机选择的,所以可将yI=h(xi),1<=i<=k视作Y中的随机元素(yi(1<=i<=k)未必不同)。但计算k个随机元素y1,y2, ••••••yk∈Y是不同的概率是一件容易的事情。依次考虑y1,y2, ••••••yk。y1可任意地选择;y2 ≠y1的概率为1-1/n;y3 ≠y1 ,y2的概率为1-2/n;••••••;yk ≠y1,y2, ••••••,yk-1的概率为1-(k-1)/n。 |
| 因此,没有碰撞的概率是(1-1/n)(1-2/n)••••••(1-(k-1)/n)。如果x是一个比较小的实数,那么1-x≈e-x,这个估计可由下式推出:e-x=1-x+x2/2!-x3/3!+ ••••••。现在估计没有碰撞的概率(1-1/n)(1-2/n)••••••(1-(k-1)/n)约为1-e-k(k-1)/2n。我们设ε是至少有一个碰撞的概率,则ε≈1-e-k(k-1)/2n,从而有k2-k≈nln(1/(1-ε)2)。去掉-k这一项,我们有k2≈nln(1/(1-ε)2),即k≈sqrt(2nln(1/(1-ε)2))。 |
| 如果我们取ε=0.5,那么k≈1.17 sqrt(n)。这表明,仅sqrt(n)个X的随机的元素就能以50%的概率产生一个碰撞。注意ε的不同选择将导致一个不同的常数因子,但k与sqrt(n)仍成正比例。 |
| 如果X是一个教室中的所有学生的集合,Y是一个非闰年的365天的集合,h(x)表示学生x的生日,这时n=365,ε=0.5,由k≈1.17 sqrt(n)可知,k≈22.3。因此,此生日问题的答案为23。 |
| 生日攻击隐含着消息摘要的长度的一个下界。一个40比特长的消息摘要是很不安全的,因为仅仅用220(大约一百万)次随机Hash可至少以1/2的概率找到一个碰撞。为了抵抗生日攻击,通常建议消息摘要的长度至少应取为128比特,此时生日攻击需要约264次Hash。安全的Hash标准的输出长度选为160比特是出于这种考虑。 |
“中间相遇法”是生日攻击的一种变形,它不比较Hash值,而是比较链中的中间变量。这种攻击主要适用于攻击具有分组链结构的Hash方案。中间相遇攻击的基本原理为:将消息分成两部分,对伪造消息的第一部分从初试值开始逐步向中间阶段产生r1个变量;对伪造消息的第二部分从Hash结果开始逐步退回中间阶段产生r2个变量。在中间阶段有一个匹配的概率与生日攻击成功的概率一样。
“模差分法”是山东大学王小云教授提出的Hash分析方法,具有较高的执行效率。模差分的算法请参考http://wenku.baidu.com/view/f0bf451414791711cc7917b5.html?from=related。
2.HashTable与HashTable退化
上面我们了解了Hash函数的特性和Hash攻击的可行性。我在这里没有详细说明攻击的算法细节,也没有给出具体的代码实现,因为这些不是本文要关注的重点,之后如果有机会我会专门讨论Hash攻击的各种方案及代码实现。下面我们来了解和Hash函数密切相关的数据结构—HashTable(参考内容:http://en.wikipedia.org/wiki/Hash_table )。
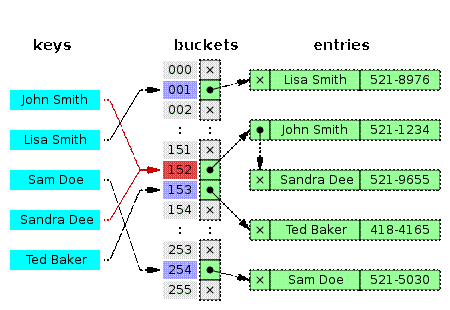
HashTable(散列表,也叫哈希表),是一种根据键值(key-value)进行直接访问的数据结构。
HashTable结合了链表和数组的双向优势,所以增、删、改、查各种操作速度都很快。在HashTable中,Hash函数的作用是通过Key得到Value的地址(数组的下标),这和我们前面说到的在安全领域保证数据完整性的Hash算法的功能有所区别,因为要返回的是数组下标,所以Hash值必须是整数。因此信息安全领域的标准Hash算法在这里就无用武之地了,不同的应用开发平台通常实现自己的Hash算法,或者使用在HashTable构造算法中常用的Hash函数,比如DJBX33A算法。
前面我们说话Hash无法避免Hash碰撞的问题,那么HashTable如何处理碰撞问题呢,通常有两种做法:开放定址法,链接法。
开放定址法(Open addressing)这种方法就是在计算一个key的哈希的时候,发现目标地址已经有值了,即发生冲突了,这个时候通过相应的函数在此地址后面的地址去找,直到没有冲突为止。这个方法常用的有线性探测,二次探测,再哈希。这种解决方法有个不好的地方就是,当发生冲突之后,会在之后的地址空间中找一个放进去,这样就有可能后来出现一个key哈希出来的结果也正好是它放进去的这个地址空间,这样就会出现非同义词的两个key发生冲突。
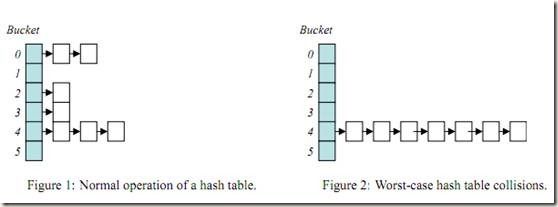
链接法(Separate chaining)链接法是通过数组和链表组合而成的。当发生冲突的时候只要将其加到对应的链表中即可。如图1-2.
图1-2
与开放定址法相比,链接法有如下几个优点:
①链接法处理冲突简单,且无堆积现象,即非同义词决不会发生冲突,因此平均查找长度较短;
②由于链接法中各链表上的结点空间是动态申请的,故它更适合于造表前无法确定表长的情况;
③开放定址法为减少冲突,要求装填因子α较小,故当结点规模较大时会浪费很多空间。而链接法中可取α≥1,且结点较大时,拉链法中增加的指针域可忽略不计,因此节省空间;
④在用链接法构造的散列表中,删除结点的操作易于实现。只要简单地删去链表上相应的结点即可。而对开放地址法构造的散列表,删除结点不能简单地将被删结点的空间置为空,否则将截断在它之后填人散列表的同义词结点的查找路径。这是因为各种开放地址法中,空地址单元(即开放地址)都是查找失败的条件。因此在 用开放地址法处理冲突的散列表上执行删除操作,只能在被删结点上做删除标记,而不能真正删除结点。
当然链接法也有其缺点,拉链法的缺点是:指针需要额外的空间,故当结点规模较小时,开放定址法较为节省空间,而若将节省的指针空间用来扩大散列表的规模,可使装填因子变小,这又减少了开放定址法中的冲突,从而提高平均查找速度。
以链接法为例,如果每次插入的值都产生碰撞,那么HashTable最终就变成了一个链表,我们称之为HashTable退化。如图1-3.
图1-3
HashTable退化成一个链表之后,性能会急剧的下降。
3.拒绝服务攻击
HashTable在所有的Web应用框架上都有应用,我们对Web应用每次发起请求所提交的参数,服务器端都会将其存储在HashTable中供后台代码调用。比如在Asp.NET应用中,我们使用Request.Form[key]和Request.QueryString[key]的方式来获取客户端提交的参数,参数就是被存储在HashTable中的,我们传入参数名称作为Key,通过Hash函数转换成对应的Value的数组下标,然后Value值被返回。
在正常的应用场景下这没什么问题,现在我们回到上面提到的HashTable退化的问题,如果客户端根据Web应用框架采用的Hash函数来通过某种Hash攻击的方式获得大量的碰撞,那么HashTable就会退化成链表,服务器有可能处理一次请求要花上十几分钟甚至几个小时的时间,一台PC机就可以搞定一台服务器,根本不用分布式攻击。当然攻击能否成功的先决条件是Web应用框架采用的Hash机制存在漏洞。如果存在这样的漏洞,攻击者可以轻而易举的实施拒绝服务攻击。
下面我们来看看现实世界中,流行的Web框架对HashTable退化的防御能力。(参考内容:http://www.nruns.com/_downloads/advisory28122011.pdf)
3.1 PHP5
PHP5的HashTable使用的函数是DJBX33A。
| DJBX33A算法,也叫time33算法,它是php、apache,、perl、bsddb的默认Hash算法。 |
| 下面的代码体现了DJBX33A算法的基本思想 uint32_t time33(char const *str, int len) { unsigned long hash = 0; for (int i = 0; i < len; i++) { hash = hash *33 + (unsigned long) str[i]; } return hash; } |
| 对于为什么使用33这个数,有这样的解释: 1到256之间的所有奇数,都能达到一个可接受的哈希分布,平均分布大概是86%。而其中33,17,31,63,127,129这几个数在面对大量的哈希运算时有一个更大的优势,就是这些数字能将乘法用位运算配合加减法替换,这样运算速度会更高。并不是所有基于DJBX33A的算法都使用33作为倍数,如Ngix使用的是time31,Tokyo Cabinet使用的是time37。 |
| PHP版本的DJBX33A算法如下所示: inline unsigned time33(char const*str, int len) |
对于DJBX33A算法,我们完全可以通过上面提到的“相等子串法”来找到碰撞,进行攻击。
目前PHP官方建议通过配置来限制表单提交的最大长度来抵御该攻击。
3.2 ASP.NET
Asp.NET使用Request.Form对象来获取表单提交的变量。内部的Hash函数是DJBX33X(Dan Bernstein's times 33, XOR)。
DJBX33X算法思想如下所示:
static ulong DJBX33X (char *arKey, uint nKeyLength)
{
ulong h = 5381;
char *arEnd = arKey + nKeyLength;
while (arKey < arEnd) {
h += (h << 5);
h ^= (ulong) *arKey++;
}
return h;
}
针对DJBX33X算法的特点,我们可以采用上面提到的中间相遇攻击的方法来寻找碰撞。
微软已经发布了针对该漏洞的补丁,如果您担心该漏洞会对您的网站造成麻烦,请更新补丁。
3.3 Java
Java 的Hash函数是对DJBX33A的改造(使用的31而不是33,另外初始值为0而不是5381),但我们仍然可以使用相等子串法来获取该Hash函数的碰撞。
基于Java的Tomcat服务器存在这样的漏洞。
3.4 其他
Python、Ruby和V8同样有这样的漏洞。