这篇文章主要介绍一下 平衡二叉树(AVL),对于 二分搜索树 来说,如果树上的 元素 是顺序 添加的,会导致数据退化成一个 链表,这样就会造成很严重的性能问题,此时就需要在 二分搜索树 的基础上,保证元素插入时平衡,在了解 AVL 之前,需要您对 二分搜索树 有一定的了解,可以参考之前的文章。
1.二分搜索树的问题
如下图所示,若向二分搜索树中添加的元素是按照 顺序 从小到大依次插入的,这样会导致最后节点退化成链表: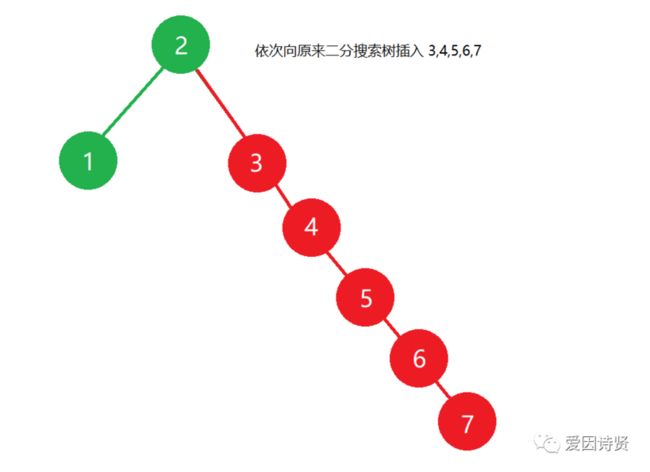
Tips:反过来依次从大到插入元素也会出现退化成
链表。
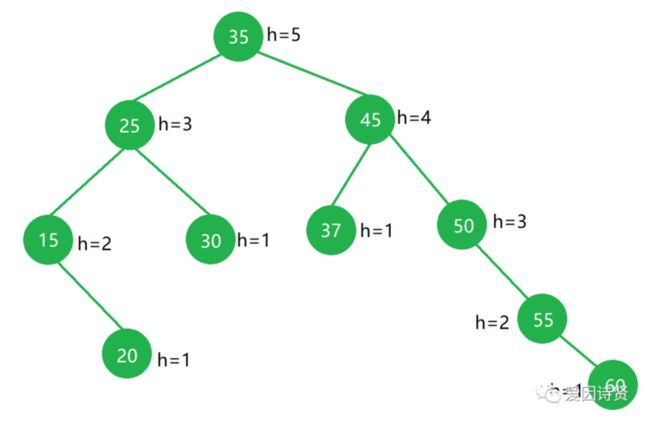
2.二叉树节点高度标注示意图
Tips:平衡因子等于左儿子高度减去右儿子高度,如45和这个节点平衡因子-2。
3.平衡二叉树特点
- 对于任何一个节点,
左儿子树和右儿子树的高度差(Δh)的绝对值不能超过1,高度差(Δh)称为平衡因子。 - 本质是带了平衡功能的
二分搜索树。 - 平衡二叉树(AVL) 的
高度(h)和节点数之间的关系是O(logn)级别的。
4.节点定义 PHP 代码
对于 二分搜索树 来说,AVL 需要在插入元素的时候保证 平衡,就需要引入节点高度(h),所以节点定义需要在 二分搜索树 节点定义的基础上增加一个 height 属性:
class AVLNode
{
public $e;
public $left = null;
public $right = null;
public $height = 1;
/**
* 构造函数 初始化节点数据
* Node constructor.
* @param $e
*/
public function __construct($e) {
$this->e = $e;
}
}5.计算平衡因子
平衡因子等于左儿子高度减去右儿子高度,代码如下:
/**
* 获取 AVL 节点的高度 h
* @param AVLNode $node
* @return int
*/
private function getHeight(AVLNode $node) {
if ($node == null) {
return 0;
}
return $node->height;
}
/**
* 获取节点平衡因子
* @param AVLNode $node
* @return int
*/
private function getBalanceFactor(AVLNode $node){
if ($node == null){
return 0;
}
return $this->getHeight($node->left) - $this->getHeight($node->right);
}6.更新节点高度
若递归插入元素时,需要更新节点高度,递归时当前节点高度 h = 1 + (左右儿子中最大h),代码如下:
/**
* 向 AVL 添加元素
* @param $e
*/
public function add($e) {
$this->root = $this->recursionAdd($this->root, $e);
}
/**
* 递归向 AVL 添加元素
* @param Node $root
* @param $e
*/
private function recursionAdd($root, $e) {
if ($root == null) { //若节点为空则添加元素 并且返回当前节点信息
$root = new AVLNode($e);
$this->size++;
} elseif ($e < $root->e) { //若元素小于当前节点元素 则向左节点递归添加元素
$root->left = $this->recursionAdd($root->left, $e);
} elseif ($e > $root->e) { //若元素大于当前节点元素 则向右节点递归添加元素
$root->right = $this->recursionAdd($root->right, $e);
} //若元素等于当前节点元素 则什么都不做
//更新节点高度
$root->height = 1 + ($this->getHeight($root->left) > $this->getHeight($root->right) ? $this->getHeight($root->left) : $this->getHeight($root->right));
return $root;
}
Tips:此处代码直接贴出之前
二分搜索树 代码添加元素方法。
7.判断二叉树是否为二分搜索树
若要判断二叉树是否为二分搜索树,则需要将二叉树中序遍历,若输出结果是按照顺序依次从小到大排列的,则表示该 二叉树 是一颗 二分搜索树,采用递归思想层序遍历然后将节点元素依次入队,代码如下,然后依次出队查看出队元素是否依次增大:
/**
* 判断二叉树是否为二分搜索树
*/
public function isBST() {
$queue = new QueueByLinkedList();
$this->inOrder($this->root, $queue);
do {
$e = $queue->dequeue();
if ($queue->getSize() > 0 && $e > $queue->getFront()) {
return false;
}
} while ($queue->getSize() > 0);
return true;
}
/**
* 中序遍历二分搜索树
*/
private function inOrder($root, $queue) {
if ($root != null) {
$this->inOrder($root->left, $queue);
$queue->enqueue($root->e);
$this->inOrder($root->right, $queue);
}
}8.判断二叉树是否为平衡二叉树(AVL)
若需要判断二叉树是否为平衡二叉树(AVL),则需要遍历二叉树,判断平衡因子 的绝对值是否大于 1,若大于 1 则不是 平衡二叉树(AVL),否则就是,代码如下,使用递归处理:
/**
* 判断二叉树是否为平衡二叉树
* @return bool
*/
public function isBalanced(): bool {
return $this->recursionIsBalanced($this->root);
}
/**
* 遍历二叉树 判断每个节点是否满足平衡因子绝对值 小于等于 1
* @param $node
* @return bool
*/
private function recursionIsBalanced($node) {
if ($node != null) {
if ($this->getBalanceFactor($node) < -1 || $this->getBalanceFactor($node) > 1) {
return false;
}
$left = $this->recursionIsBalanced($node->left);
$right = $this->recursionIsBalanced($node->right);
if (!$left || !$right) {
return false;
}
}
return true;
}9.添加元素时的平衡原理
9.1 添加元素影响节点示意图
若向 二叉树 中添加元素,则只需判断该节点的 父亲节点 和 祖先节点 的 平衡因子 即可,如下图所示:
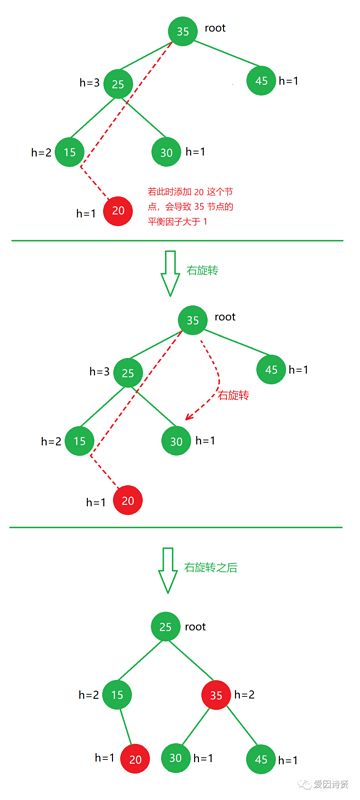
9.2 添加元素在左儿子左侧时右旋转示意图(LL)
Tips:如图所示,新添加的元素是在左儿子的左侧,此时右旋转可以纠正平衡。
9.3 添加元素在右儿子右侧时左旋转示意图(RR)
Tips:如图所示,新添加的元素是在右儿子的右侧,此时左旋转可以纠正平衡。
9.4 添加元素在左儿子右侧时先把左儿子左旋转再右旋转该节点(LR)
Tips:如图所示,新添加的元素是在左儿子的右侧,此时先把左儿子左旋转,再右旋转该节点可以纠正平衡。
9.5 添加元素在右儿子左侧时先把右儿子右旋转再左旋转该节点(RL)
Tips:如图所示,新添加的元素是在右儿子的左侧,此时先把右儿子右旋转,再左旋转该节点可以纠正平衡。
9.3 右旋转代码
/** 对节点 r 进行右旋转操作,返回旋转后的节点
* 35($r) 25($m)
* / /
* 25($m) 45 15($n) 35($r)
* / 对35节点右旋转之后 / /
* 15($n) 30($a) 10 20 30($a) 45
* /
* 10 20
* 对应的关系如下:
* $m = $r->left;
* $a = $m->right;
* $m->right = $r;
* $r->left = $a;
*/
private function rightRotate($r)
{
$m = $r->left;
$a = $m->right;
$m->right = $r;
$r->left = $a;
//右旋转之后只需要更新 $m 节点和 $r 节点的高度
$r->height = $this->getHeight($r);
$m->height = $this->getHeight($m);
return $m;
}9.5 左旋转代码
/** 对节点 r 进行右旋转操作,返回旋转后的节点
* 35($r) 25($m)
* / /
* 25($m) 45 15($n) 35($r)
* / 对35节点右旋转之后 / /
* 15($n) 30($a) 10 20 30($a) 45
* /
* 10 20
* 对应的关系如下:
* $m = $r->left;
* $a = $m->right;
* $m->right = $r;
* $r->left = $a;
*/
private function rightRotate($r)
{
$m = $r->left;
$a = $m->right;
$m->right = $r;
$r->left = $a;
//右旋转之后只需要更新 $m 节点和 $r 节点的高度
$r->height = $this->getHeight($r);
$m->height = $this->getHeight($m);
return $m;
}9.6 完整PHP代码
root = null;
$this->size;
}
/** 对节点 r 进行右旋转操作,返回旋转后的节点
* 35($r) 25($m)
* / /
* 25($m) 45 15($n) 35($r)
* / 对35节点右旋转之后 / /
* 15($n) 30($a) 10 20 30($a) 45
* /
* 10 20
* 对应的关系如下:
* $m = $r->left;
* $a = $m->right;
* $m->right = $r;
* $r->left = $a;
*/
private function rightRotate($r) {
$m = $r->left;
$a = $m->right;
$m->right = $r;
$r->left = $a;
//右旋转之后只需要更新 $m 节点和 $r 节点的高度
$r->height = $this->getHeight($r);
$m->height = $this->getHeight($m);
return $m;
}
/** 对节点 r 进行左旋转操作,返回旋转后的节点
* 35($r) 45($m)
* / /
* 30 45($m) 35($n) 55($r)
* / 对35节点左旋转之后 / /
* 40($a) 55($n) 30 40 50($a) 60
* /
* 50 60
* 对应的关系如下:
* $m = $r->right;
* $a = $m->left;
* $m->left = $r;
* $r->right = $a;
*/
private function leftRotate($r) {
$m = $r->right;
$a = $m->left;
$m->left = $r;
$r->right = $a;
//左旋转之后只需要更新 $m 节点和 $r 节点的高度
$r->height = $this->getHeight($r);
$m->height = $this->getHeight($m);
return $m;
}
/**
* 判断二叉树是否为二分搜索树
*/
public function isBST(): bool {
$queue = new QueueByLinkedList();
$this->inOrder($this->root, $queue);
do {
$e = $queue->dequeue();
if ($queue->getSize() > 0 && $e > $queue->getFront()) {
return false;
}
} while ($queue->getSize() > 0);
return true;
}
/**
* 判断二叉树是否为平衡二叉树
* @return bool
*/
public function isBalanced(): bool {
return $this->recursionIsBalanced($this->root);
}
/**
* 遍历二叉树 判断每个节点是否满足平衡因子绝对值 小于等于 1
* @param $node
* @return bool
*/
private function recursionIsBalanced($node) {
if ($node != null) {
if ($this->getBalanceFactor($node) < -1 || $this->getBalanceFactor($node) > 1) {
return false;
}
$left = $this->recursionIsBalanced($node->left);
$right = $this->recursionIsBalanced($node->right);
if (!$left || !$right) {
return false;
}
}
return true;
}
/**
* 中序遍历二分搜索树
*/
private function inOrder($root, $queue) {
if ($root != null) {
$this->inOrder($root->left, $queue);
$queue->enqueue($root->e);
$this->inOrder($root->right, $queue);
}
}
/**
* 获取 AVL 节点的高度 h
* @param AVLNode $node
* @return int
*/
private function getHeight($node) {
if ($node == null) {
return 0;
}
return $node->height;
}
/**
* 获取当前搜索树元素个数
* @return mixed
*/
public function getSize() {
return $this->size;
}
/**
* 判断当前 AVL 是否为空
* @return bool
*/
public function isEmpty(): bool {
return $this->size == 0;
}
/**
* 向 AVL 添加元素
* @param $e
*/
public function add($e) {
$this->root = $this->recursionAdd($this->root, $e);
}
/**
* 递归向 AVL 添加元素
* @param Node $root
* @param $e
*/
private function recursionAdd($root, $e) {
if ($root == null) { //递归到底的情况,若节点为空则添加元素 并且返回当前节点信息
$root = new AVLNode($e);
$this->size++;
} elseif ($e < $root->e) { //若元素小于当前节点元素 则向左节点递归添加元素
$root->left = $this->recursionAdd($root->left, $e);
} elseif ($e > $root->e) { //若元素大于当前节点元素 则向右节点递归添加元素
$root->right = $this->recursionAdd($root->right, $e);
} //若元素等于当前节点元素 则什么都不做
//更新节点高度
$root->height = 1 + ($this->getHeight($root->left) > $this->getHeight($root->right) ? $this->getHeight($root->left) : $this->getHeight($root->right));
//平衡的维护
$balanceFactor = $this->getBalanceFactor($root);
//LL 添加元素在左儿子左侧
if ($balanceFactor > 1 && $this->getBalanceFactor($root->left) >= 0) {
$this->rightRotate($root);
}
//RR 添加元素在右儿子右侧
if ($balanceFactor < -1 && $this->getBalanceFactor($root->left) <= 0) {
$this->leftRotate($root);
}
//LR 添加元素在左儿子右侧
if ($balanceFactor > 1 && $this->getBalanceFactor($root->right) < 0) {
//先把左儿子左旋转
$root->left = $this->leftRotate($root->left);
//再把该节点右旋转
$root = $this->rightRotate($root);
}
//RL 添加元素在右儿子左侧
if ($balanceFactor < -1 && $this->getBalanceFactor($root->right) < 0) {
//先把右儿子右旋转
$root->right = $this->leftRotate($root->right);
//再把该节点左旋转
$root = $this->leftRotate($root);
}
return $root;
}
/**
* 获取节点平衡因子
* @param AVLNode $node
* @return int
*/
private function getBalanceFactor($node) {
if ($node == null) {
return 0;
}
return $this->getHeight($node->left) - $this->getHeight($node->right);
}
/**
* 判断 AVL 是否包含某个元素
* @param $e
* @return bool
*/
public function contains($e): bool {
return $this->recursionContains($this->root, $e);
}
/**
* 递归判断 AVL 是否包含某元素
* @param $root
* @param $e
* @return bool
*/
private function recursionContains($root, $e): bool {
if ($root == null) { //若当前节点为空 则表示不存在元素 $e
return false;
} elseif ($e == $root->e) { //若 $e 等于当前节点元素,则表示树包含元素 $e
return true;
} elseif ($e < $root->e) { //若 $e 小于当前节点元素,则去左儿子树递归查询是否包含节点
return $this->recursionContains($root->left, $e);
} else { //若 $e 大于当前节点元素,则去右儿子树递归查询是否包含节点
return $this->recursionContains($root->right, $e);
}
}
/**
* 前序遍历
*/
public function preTraversal() {
$this->recursionPreTraversal($this->root, 0);
}
/**
* 前序遍历的递归
*/
public function recursionPreTraversal($root, $sign_num) {
echo $this->getSign($sign_num);//打印深度
if ($root == null) {
echo "null
";
return;
}
echo $root->e . "
"; //打印当前节点元素
$this->recursionPreTraversal($root->left, $sign_num + 1);
$this->recursionPreTraversal($root->right, $sign_num + 1);
}
/**
* 中序遍历
*/
public function midTraversal() {
$this->recursionMidTraversal($this->root, 0);
}
/**
* 中序遍历的递归
*/
public function recursionMidTraversal($root, $sign_num) {
if ($root == null) {
echo $this->getSign($sign_num);//打印深度
echo "null
";
return;
}
$this->recursionMidTraversal($root->left, $sign_num + 1);
echo $this->getSign($sign_num);//打印深度
echo $root->e . "
";
$this->recursionMidTraversal($root->right, $sign_num + 1);
}
/**
* 后序遍历
*/
public function rearTraversal() {
$this->recursionRearTraversal($this->root, 0);
}
/**
* 后序遍历的递归
*/
public function recursionRearTraversal($root, $sign_num) {
if ($root == null) {
echo $this->getSign($sign_num);//打印深度
echo "null
";
return;
}
$this->recursionRearTraversal($root->left, $sign_num + 1);
$this->recursionRearTraversal($root->right, $sign_num + 1);
echo $this->getSign($sign_num);//打印深度
echo $root->e . "
";
}
/**
* 前序遍历压栈实现
*/
public function preTraversalByStack() {
$stack = new StackByLinkedList();
//将根节点压入栈
$stack->push($this->root);
while (!$stack->isEmpty()) {
//出栈
$node = $stack->pop();
if ($node != null) { //若出栈的当前节点不是空
echo $node->e . "
"; //先入栈
//先入栈右儿子
$stack->push($node->right);
//然后入栈左儿子
$stack->push($node->left);
} else { //若是空
echo "null
";
}
}
}
/**
* 中序遍历压栈实现
*/
public function midTraversalByStack() {
$stack = new StackByLinkedList();
//将根节点压入栈
$stack->push($this->root);
//循环依次出栈
$node = $stack->pop();
do {
if ($node != null) { //若出栈的当前节点不是空
//先入栈右儿子
$stack->push($node->right);
echo $node->e . "
"; //然后打印当前节点信息
//最后入栈左儿子
$stack->push($node->left);
} else { //若是空
echo "null
";
}
//继续出栈
$node = $stack->pop();
} while (!$stack->isEmpty());
}
/**
* 层序遍历实现
*/
public function tierTraversalByLinkedList() {
$queue = new QueueByLinkedList();
//将根节点入队
$queue->enqueue($this->root);
//循环依次出队
$node = $queue->dequeue();
do {
if ($node != null) { //若出栈的当前节点不是空
echo $node->e . "
"; //然后打印当前节点信息
$queue->enqueue($node->left);//左儿子入队
$queue->enqueue($node->right);//右儿子入队
} else { //若是空
echo "null
";
}
//继续出队
$node = $queue->dequeue();
} while (!$queue->isEmpty());
}
/**
* 获取最小元素
* @return mixed
*/
public function getMin() {
return $this->getMinNode($this->root)->e;
}
/**
* 获取某颗树最小元素节点
* @param $root
* @return mixed
*/
private function getMinNode($root) {
for ($node = $root; $node != null; $node = $node->left) {
if ($node->left != null) {
$root = $node->left;
} else {
$root = $node;
}
}
return $root;
}
/**
* 获取最大元素
* @return mixed
*/
public function getMax() {
return $this->getMaxNode($this->root)->e;
}
/**
* 获取某颗树最大元素节点
* @param $root
* @return mixed
*/
private function getMaxNode($root) {
for ($node = $root; $node != null; $node = $node->right) {
if ($node->right != null) {
$root = $node->right;
} else {
$root = $node;
}
}
return $root;
}
/**
* 删除 AVL 元素
* @param $e
*/
public function remove($e) {
$this->root = $this->recursionRemove($this->root, $e);
}
/**
* 递归删除 AVL 元素
* @param $root
* @param $e
*/
private function recursionRemove($root, $e) {
if ($root != null) {
if ($e == $root->e) {
$root = $this->joinRemoveNode($root);
} elseif ($e < $root->e) {
$root->left = $this->recursionRemove($root->left, $e);
} else {
$root->right = $this->recursionRemove($root->right, $e);
}
}
return $root;
}
/**
* 拼接删除节点 返回新节点
*/
private function joinRemoveNode($root) {
if ($root->left != null && $root->right == null) {
$root = $root->left;
} elseif ($root->left == null && $root->right != null) {
$root = $root->right;
} else {
$leftMax = $this->getMaxNode($root->left);
$leftMax->right = $root->right;
$root = $root->left;
}
return $root;
}
public function getSign($num) {
$str = "";
for ($i = 0; $i < $num; $i++) {
$str .= "-----";
}
return $str;
}
}
class AVLNode
{
public $e;
public $left = null;
public $right = null;
public $height = 1;
/**
* 构造函数 初始化节点数据
* Node constructor.
* @param $e
*/
public function __construct($e) {
$this->e = $e;
}
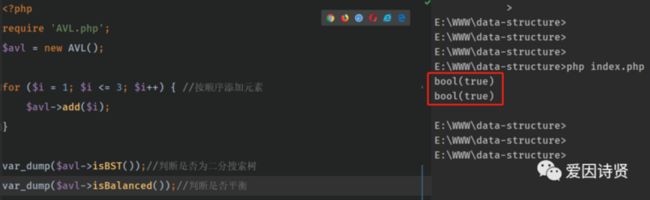
}10.输出演示
add($i);
}
var_dump($avl->isBST());//判断是否为二分搜索树
var_dump($avl->isBalanced());//判断是否平衡代码仓库 :https://gitee.com/love-for-po...
扫码关注爱因诗贤
![]()