Flash/Flex学习笔记(55):背面剔除与 3D 灯光
Animation in ActionScript3.0 这本书总算快学完了,今天继续:上一回Flash/Flex学习笔记(50):3D线条与填充 里,我们知道任何一个3D多面体上的某一个面,都可以分解为多个三角形的组合。比立方体为例,每个面都由二个三角形组成,但在那一篇的示例中明显有一个问题:不管立方体的某一个面是不是应该被人眼看见(比如转到背面的部分,应该是看不见的),这一面都被绘制出来了。
在这一篇的学习中,我将带大家一起学习如何将背面(即看不见的面)删除掉,即所谓的“背面剔除”。
先做一些预备知识的铺垫:立方体中每个面都有一个"外面"和"里面"。外面即正对观察者向外的这一面,里面指朝向立方体内部的这一面。我们在3D编程里,通常指的都是“外面”
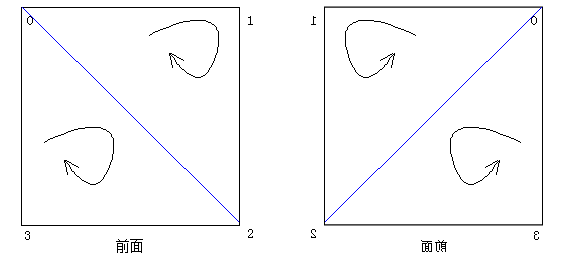
如上图:这是立方体的前面,分解为0-1-2和0-2-3二个三角形(注意三个顶点的顺序为"顺时针"方向),当立方体的"前面"旋转到"后面"所处位置时,三角形的顶点顺序由“顺时针”改变为“逆时针”。
言外之意:如果我们能判断出某个三角形的顶点顺序为“逆时针”时,这个三角形肯定处于背面,这时应该将它隐藏或不绘制。
所以,如果我们在构建立方体每个面的三角形时,都遵守上面的“三角形顶点顺时针法则”,那么上面的解决办法应该就能满足要求了,回顾一下立方体三角形数组的构建代码:
//前 triangles[0] = new Triangle(points[0], points[1], points[2], 0x6666cc); triangles[1] = new Triangle(points[0], points[2], points[3], 0x6666cc); //上 triangles[2] = new Triangle(points[0], points[5], points[1], 0x66cc66); triangles[3] = new Triangle(points[0], points[4], points[5], 0x66cc66); //后 triangles[4] = new Triangle(points[4], points[6], points[5], 0xcc6666); triangles[5] = new Triangle(points[4], points[7], points[6], 0xcc6666); //底 triangles[6] = new Triangle(points[3], points[2], points[6], 0xcc66cc); triangles[7] = new Triangle(points[3], points[6], points[7], 0xcc66cc); //右 triangles[8] = new Triangle(points[1], points[5], points[6], 0x66cccc); triangles[9] = new Triangle(points[1], points[6], points[2], 0x66cccc); //左 triangles[10] =new Triangle(points[4], points[0], points[3], 0xcccc66); triangles[11] =new Triangle(points[4], points[3], points[7], 0xcccc66);
建议大家去买一个立体魔方玩具,每个点按照上一篇里的顶点数字拿笔标记起来,对比上面的代码发现,这样的代码正好是遵守这一规则的,当然代码不必完全跟这一样,比如:
//前 triangles[0] = new Triangle(points[0], points[1], points[2], 0x6666cc); triangles[1] = new Triangle(points[0], points[2], points[3], 0x6666cc);
也可以写成:
triangles[0] = new Triangle(points[1],points[2],points[0],0x6666cc); triangles[1] = new Triangle(points[0],points[2],points[3],0x6666cc);
或
triangles[0] = new Triangle(points[1],points[2],points[3],0x6666cc); triangles[1] = new Triangle(points[1],points[3],points[0],0x6666cc);
只要满足顺时针规则即可.ok,已经成功了一半,如何判断三角形处于背面?
//判断是否在背面
private function isBackFace():Boolean {
var cax:Number = pointC.screenX - pointA.screenX;
var cay:Number = pointC.screenY - pointA.screenY;
var bcx:Number = pointB.screenX - pointC.screenX;
var bcy:Number = pointB.screenY - pointC.screenY;
return cax * bcy > cay * bcx;
}
在Triangle.cs中增加这个私有方法即可(我也不知道怎么来的,反正这个函数确实管用,就当公式死记下来好了.)
最后一个小问题:在旋转的过程中,三角形的三个顶点“z轴深度”(zPos值)都在变化,有可能出现某个三角形的顶点挡住了另外一个三角形的顶点。所以我们还得解决三角形的z轴排序问题,这里有一个法则,可以把三个顶点中离观察者最近的一个顶zPos值,认为是三角形的z轴深度,所以Triangle.cs中还得增加一个z轴属性:depth,最终Triangle.cs的内容如下:
package {
import flash.display.Graphics;
public class Triangle {
private var pointA:Point3D;
private var pointB:Point3D;
private var pointC:Point3D;
private var color:uint;
public function Triangle(a:Point3D,b:Point3D,c:Point3D,color:uint) {
pointA = a;
pointB = b;
pointC = c;
this.color = color;
}
public function draw(g:Graphics):void {
//如果是背面,则不绘制
if (isBackFace()) {
return;
}
g.beginFill(color);
g.moveTo(pointA.screenX,pointA.screenY);
g.lineTo(pointB.screenX,pointB.screenY);
g.lineTo(pointC.screenX,pointC.screenY);
g.lineTo(pointA.screenX,pointA.screenY);
g.endFill();
}
//判断是否在背面
private function isBackFace():Boolean {
// 见 http://www.jurjans.lv/flash/shape.html
var cax:Number = pointC.screenX - pointA.screenX;
var cay:Number = pointC.screenY - pointA.screenY;
var bcx:Number = pointB.screenX - pointC.screenX;
var bcy:Number = pointB.screenY - pointC.screenY;
return cax * bcy > cay * bcx;
}
//取得三角形所在的z轴深度(以三个顶点中离观察者最近的点为准)
public function get depth():Number {
var zpos:Number = Math.min(pointA.z,pointB.z);
zpos = Math.min(zpos,pointC.z);
return zpos;
}
}
}
罗嗦了一堆,激动人心的时刻终于来了,原来的立方体示例代码中,只要增加一行代码:
function EnterFrameHandler(e:Event):void {
var dx:Number = mouseX - vpX;
var dy:Number = mouseY - vpY;
var angleX:Number = dy * 0.001;
var angleY:Number = dx * 0.001;
var angleZ:Number = Math.sqrt(dx * dx + dy * dy) * 0.0005;
if (dx > 0) {
angleZ *= -1;
}
for (var i:uint = 0; i < pointNum; i++) {
var point:Point3D = points[i];
point.rotateX(angleX);
point.rotateY(angleY);
point.rotateZ(angleZ);
}
triangles.sortOn("depth", Array.DESCENDING | Array.NUMERIC);//增加三角形数组的z轴排序
graphics.clear();
for (i = 0; i < triangles.length; i++) {
triangles[i].draw(graphics);
}
}
编译运行,最终将得到一个仅2.7k的swf动画,而且还带有鼠标交互的3D立方体,cool 吧!
其它示例修改后,效果如下:
3D光线:
这部分内容比较难理解(需要有一定的线性代数基础),先上最终的效果图(光源的位置在左顶点,z轴“-100”处--即flash动画左上顶点距离屏幕垂直向外100的地方,需要一点想象力)
理解原理需要线性代数中“向量的矢量积”以及“向量的数量积”、“向量夹角计算”这三个关键概念(不熟悉的童鞋们,请先下载“高等数学-07章空间解释几何与向量代数.pdf”回忆一下数学老师教给我们的东西,有点痛苦!)
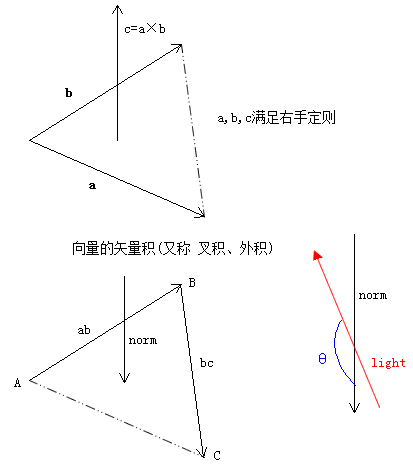
如上图,对于每个三角形必须先确定其“法向”向量norm,norm即为向量ab与向量bc的叉积。然后光源light本身也是一个向量,向量light与向量norm会形成一个夹角θ,θ的取值范围在0~PI(即180度)之间,θ为180度时即为正面直射,θ为0度时即为背面照射(实际上小于等于90度时,已经照不到了),直射意味着三角形所在平面颜色应该正常显示(最明亮),背面或照不到时,应该颜色变暗,接近黑色。
关于这个结论,可以先来看下面的演示:(光源的位置我设置为动画中心,距离屏幕向外100px的位置,即正对着屏幕中心照射)
一步一步来,先定义Light向量类:
package {
public class Light {
public var x:Number;
public var y:Number;
public var z:Number;
private var _brightness:Number;
public function Light(x:Number=-200,y:Number=-200,z:Number=-200,brightness:Number=1) {
//light向量的空间坐标
this.x = x;
this.y = y;
this.z = z;
//亮度
this.brightness = brightness;
}
public function set brightness(b:Number):void {
//亮度值通常要求在0与1之间
_brightness = Math.max(b,0);
_brightness = Math.min(_brightness,1);
}
public function get brightness():Number {
return _brightness;
}
}
}
那么,如果计算向量的矢量积,以及夹角呢?先给出数学公式:
叉积公式:
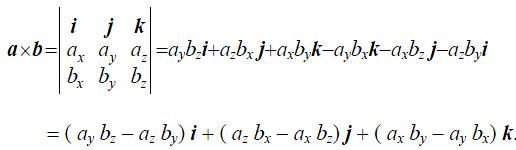
夹角公式

点积(也称数量积或内积)公式
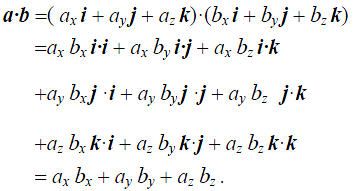
ok,理论知识准备得差不多了,下面来改造Triangle三角形基类:
package {
import flash.display.Graphics;
public class Triangle {
private var pointA:Point3D;
private var pointB:Point3D;
private var pointC:Point3D;
private var color:uint;
public var light:Light;//每个三角形增加一个光源Light
public function Triangle(a:Point3D,b:Point3D,c:Point3D,color:uint) {
pointA = a;
pointB = b;
pointC = c;
this.color = color;
}
public function draw(g:Graphics):void {
if (isBackFace()) {
return;
}
g.beginFill(getAdjustedColor());//★★★这里改为根据光线的角度来动态填充颜色
g.moveTo(pointA.screenX,pointA.screenY);
g.lineTo(pointB.screenX,pointB.screenY);
g.lineTo(pointC.screenX,pointC.screenY);
g.lineTo(pointA.screenX,pointA.screenY);
g.endFill();
}
//★★★根据光线得到动态调整后的颜色
private function getAdjustedColor():uint {
//取出红,绿,蓝三色分量
var red:Number = color >> 16;
var green:Number = color >> 8 & 0xff;
var blue:Number = color & 0xff;
var lightFactor:Number = getLightFactor();//★★★根据光线得到的颜色调整因子!!! 这是关键!
red *= lightFactor;
green *= lightFactor;
blue *= lightFactor;
return red << 16 | green << 8 | blue;
}
//根据光线得到的颜色调整因子(最难理解的的一个函数)
private function getLightFactor():Number {
var ab:Object = new Object();
ab.x = pointA.x - pointB.x;
ab.y = pointA.y - pointB.y;
ab.z = pointA.z - pointB.z;
var bc:Object = new Object();
bc.x = pointB.x - pointC.x;
bc.y = pointB.y - pointC.y;
bc.z = pointB.z - pointC.z;
var norm:Object = new Object();
//计算法向向量norm的坐标值
norm.x = (ab.y * bc.z) - (ab.z * bc.y);
norm.y = -((ab.x * bc.z) - (ab.z * bc.x));
norm.z = (ab.x * bc.y) - (ab.y * bc.x);
//向量norm与向量light的点积(数量积)
var dotProd:Number = norm.x * light.x + norm.y * light.y + norm.z * light.z;
//向量norm的模长
var normMag:Number = Math.sqrt(norm.x * norm.x + norm.y * norm.y + norm.z * norm.z);
//向量light的模长
var lightMag:Number = Math.sqrt(light.x * light.x + light.y * light.y + light.z * light.z);
//夹角angle
var angle:Number = Math.acos(dotProd / (normMag * lightMag);
return (angle / Math.PI) * light.brightness; //夹角除取值范围最大值PI,将得到一个0到1之间的小数,然后再乘light的亮度值,即得到最终的光线调整因子
}
//是否处于背面
private function isBackFace():Boolean {
var cax:Number = pointC.screenX - pointA.screenX;
var cay:Number = pointC.screenY - pointA.screenY;
var bcx:Number = pointB.screenX - pointC.screenX;
var bcy:Number = pointB.screenY - pointC.screenY;
return cax * bcy > cay * bcx;
}
//z轴深度
public function get depth():Number {
var zpos:Number = Math.min(pointA.z,pointB.z);
zpos = Math.min(zpos,pointC.z);
return zpos;
}
}
}
可以看到,我们几乎把所有的处理工作都放在Triangle.cs中完成了,好好体会一下。这一切完成之后,主动画中就能自动体现出3D光线的效果了么?No,我们还没给立方体添加光源呢!不过这个很容易,改一个地方即可:
function Init():void {
//前面四个点
points[0] = new Point3D(-50,-50,-50);
points[1] = new Point3D(50,-50,-50);
points[2] = new Point3D(50,50,-50);
points[3] = new Point3D(-50,50,-50);
//后面四个点
points[4] = new Point3D(-50,-50,50);
points[5] = new Point3D(50,-50,50);
points[6] = new Point3D(50,50,50);
points[7] = new Point3D(-50,50,50);
for (var i:uint = 0; i < pointNum; i++) {
points[i].setVanishingPoint(vpX, vpY);
points[i].setCenter(0, 0, 50);
}
//根据顶点赋值三角形数组
triangles = new Array();
var _t:Number = 0xFF0000;
//前面
triangles[0] = new Triangle(points[1],points[2],points[0],_t);
triangles[1] = new Triangle(points[0],points[2],points[3],_t);
_t = 0xFF0000;;
//后面
triangles[4] = new Triangle(points[5],points[4],points[6],_t);
triangles[5] = new Triangle(points[4],points[7],points[6],_t);
_t = 0x00FF00;;
//上面
triangles[2] = new Triangle(points[1],points[0],points[4],_t);
triangles[3] = new Triangle(points[1],points[4],points[5],_t);
_t = 0x00FF00;;
//下面
triangles[6] = new Triangle(points[3],points[2],points[6],_t);
triangles[7] = new Triangle(points[3],points[6],points[7],_t);
_t = 0x0000FF;
//右面
triangles[8] = new Triangle(points[2],points[1],points[5],_t);
triangles[9] = new Triangle(points[2],points[5],points[6],_t);
_t = 0x0000FF;
//左面
triangles[10] = new Triangle(points[4],points[0],points[3],_t);
triangles[11] = new Triangle(points[4],points[3],points[7],_t);
//★★★只要增加下面的代码,给每个三角形赋值同样的光源实例即可!
var light:Light = new Light(-275,-200,-150);
for (i = 0; i < triangles.length; i++) {
triangles[i].light = light;
}
addEventListener(Event.ENTER_FRAME, EnterFrameHandler);
stage.addEventListener(KeyboardEvent.KEY_DOWN, KeyDownHandler);
}
注意打星号的部分,只需要给三角形数组中的每个三角形赋值同样的光源实例即可,其它地方都不用动。
总算写完了,累啊,这一章确实有些难度,想起了毛主席的经典语录:“学好数理化,走遍天下都不怕!”