- 作者:小漾
- 来源:https://github.com/suukii/91-...
大家好,我是 lucifer,众所周知,我是一个小前端 (不是) 。其实,我是 lucifer 的 1379 号迷妹观察员,我是一粒纳米前端。(不要回答,不要回答,不要回答!!!)
这是第一次投稿,所以可以废话几句,说一下我为什么做题和写题解。刚开始做算法题的时候,只是纯粹觉得好玩,所以不仅没有刷题计划,写题解也只是随便记下几笔,几个月后自己也看不懂的那种。一次偶然机会发现了 lucifer 的明星题解仓库,是找到了 onepiece 的感觉。受他的启发,我也开始写些尽量能让人看懂的题解,虽然还赶不上 lucifer,但跟自己比总算是有了些进步。
身为迷妹观察员,lucifer 的 91 天学算法当然是不能错过的活动,现在活动的第二期正在 热进行中,有兴趣的同学了解一下呀。言归正传,跟着 91 课程我不再是漫无目的,而是计划清晰,按照课程安排的专题来做题,这样不仅更有利于了解某一类题涉及的相关知识,还能熟悉这类题的套路,再次遇见相似题型也能更快有思路。
废话就这么多,以下是正文部分。等等,还有最后一句,上面的"不要回答"是个三体梗,不知道有没有人 GET 到我。
今天给大家带来一道力扣简单题,官方题解只给出了一种最优解。本文比较贪心,打算带大家用四种姿势来解决这道题。
题目描述
题目地址:https://leetcode-cn.com/probl...
给定一个字符串 S 和一个字符 C。返回一个代表字符串 S 中每个字符到字符串 S 中的字符 C 的最短距离的数组。
示例 1:
输入: S = "loveleetcode", C = 'e'
输出: [3, 2, 1, 0, 1, 0, 0, 1, 2, 2, 1, 0]
说明:
字符串 S 的长度范围为 [1, 10000]。
C 是一个单字符,且保证是字符串 S 里的字符。
S 和 C 中的所有字母均为小写字母。解法 1:中心扩展法
思路
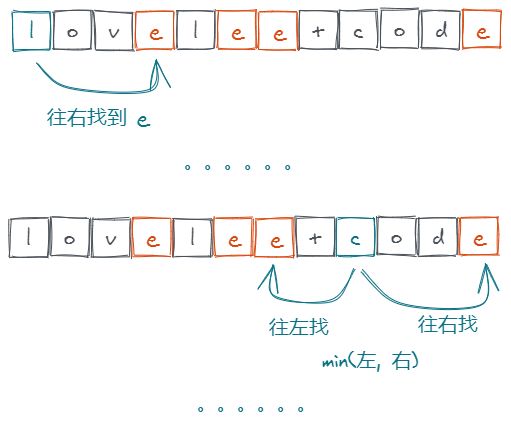
这是最符合直觉的思路,对每个字符分别进行如下处理:
- 从当前下标出发,分别向左、右两个方向去寻找目标字符
C。 - 只在一个方向找到的话,直接计算字符距离。
- 两个方向都找到的话,取两个距离的最小值。
复杂度分析
我们需要对每一个元素都进行一次扩展操作,因此时间复杂度就是 $N$ * 向两边扩展的总时间复杂度。
而最坏的情况是目标字符 C 在字符串 S 的左右两个端点位置,这个时候时间复杂度是 $O(N)$,因此总的时间复杂度就是 $O(N^2)$
- 时间复杂度:$O(N^2)$,N 为 S 的长度。
- 空间复杂度:$O(1)$。
代码
JavaScript Code
/**
* @param {string} S
* @param {character} C
* @return {number[]}
*/
var shortestToChar = function (S, C) {
// 结果数组 res
var res = Array(S.length).fill(0);
for (let i = 0; i < S.length; i++) {
// 如果当前是目标字符,就什么都不用做
if (S[i] === C) continue;
// 定义两个指针 l, r 分别向左、右两个方向寻找目标字符 C,取最短距离
let l = i,
r = i,
shortest = Infinity;
while (l >= 0) {
if (S[l] === C) {
shortest = Math.min(shortest, i - l);
break;
}
l--;
}
while (r < S.length) {
if (S[r] === C) {
shortest = Math.min(shortest, r - i);
break;
}
r++;
}
res[i] = shortest;
}
return res;
};解法 2:空间换时间
思路
空间换时间是编程中很常见的一种 trade-off (反过来,时间换空间也是)。
因为目标字符 C 在 S 中的位置是不变的,所以我们可以提前将 C 的所有下标记录在一个数组 cIndices 中。
然后遍历字符串 S 中的每个字符,到 cIndices 中找到距离当前位置最近的下标,计算距离。
复杂度分析
和上面方法类似,只是向两边扩展的动作变成了线性扫描 cIndices,因此时间复杂度就是 $N$ * 线性扫描 cIndices的时间复杂度。
- 时间复杂度:$O(N*K)$,N 是 S 的长度,K 是字符
C在字符串中出现的次数。由于 $K <= N$。因此时间上一定是优于上面的解法的。 - 空间复杂度:$O(K)$,K 为字符
C出现的次数,这是记录字符C出现下标的辅助数组消耗的空间。
实际上,由于 cIndices 是一个单调递增的序列,因此我们可以使用二分来确定最近的 index,时间可以优化到 $N*logK$,这个就留给各位来解决吧。如果对二分不熟悉的,可以看看我往期的《二分专题》
代码
JavaScript Code
/**
* @param {string} S
* @param {character} C
* @return {number[]}
*/
var shortestToChar = function (S, C) {
// 记录 C 字符在 S 字符串中出现的所有下标
var cIndices = [];
for (let i = 0; i < S.length; i++) {
if (S[i] === C) cIndices.push(i);
}
// 结果数组 res
var res = Array(S.length).fill(Infinity);
for (let i = 0; i < S.length; i++) {
// 目标字符,距离是 0
if (S[i] === C) {
res[i] = 0;
continue;
}
// 非目标字符,到下标数组中找最近的下标
for (const cIndex of cIndices) {
const dist = Math.abs(cIndex - i);
// 小小剪枝一下
// 注:因为 cIndices 中的下标是递增的,后面的 dist 也会越来越大,可以排除
if (dist >= res[i]) break;
res[i] = dist;
}
}
return res;
};解法 3:贪心
思路
其实对于每个字符来说,它只关心离它最近的那个 C 字符,其他的它都不管。所以这里还可以用贪心的思路:
- 先
从左往右遍历字符串S,用一个数组 left 记录每个字符左侧出现的最后一个C字符的下标; - 再
从右往左遍历字符串S,用一个数组 right 记录每个字符右侧出现的最后一个C字符的下标; - 然后同时遍历这两个数组,计算距离最小值。
优化 1
再多想一步,其实第二个数组并不需要。因为对于左右两侧的 C 字符,我们也只关心其中距离更近的那一个,所以第二次遍历的时候可以看情况覆盖掉第一个数组的值:
- 字符左侧没有出现过
C字符 i - left>right - i(i 为当前字符下标,left 为字符左侧最近的C下标,right 为字符右侧最近的C下标)
如果出现以上两种情况,就可以进行覆盖,最后再遍历一次数组计算距离。
优化 2
如果我们是直接记录 C 与当前字符的距离,而不是记录 C 的下标,还可以省掉最后一次遍历计算距离的过程。
复杂度分析
上面我说了要开辟一个数组。而实际上题目也要返回一个数组,这个数组的长度也恰好是 $N$,这个空间是不可避免的。因此我们直接利用这个数组,而不需要额外开辟空间,因此这里空间复杂度是 $O(1)$,而不是 $O(N)$,具体可以看下方代码区。
- 时间复杂度:$O(N)$,N 是 S 的长度。
- 空间复杂度:$O(1)$。
代码
JavaScript Code
/**
* @param {string} S
* @param {character} C
* @return {number[]}
*/
var shortestToChar = function (S, C) {
var res = Array(S.length);
// 第一次遍历:从左往右
// 找到出现在左侧的 C 字符的最后下标
for (let i = 0; i < S.length; i++) {
if (S[i] === C) res[i] = i;
// 如果左侧没有出现 C 字符的话,用 Infinity 进行标记
else res[i] = res[i - 1] === void 0 ? Infinity : res[i - 1];
}
// 第二次遍历:从右往左
// 找出现在右侧的 C 字符的最后下标
// 如果左侧没有出现过 C 字符,或者右侧出现的 C 字符距离更近,就更新 res[i]
for (let i = S.length - 1; i >= 0; i--) {
if (res[i] === Infinity || res[i + 1] - i < i - res[i]) res[i] = res[i + 1];
}
// 计算距离
for (let i = 0; i < res.length; i++) {
res[i] = Math.abs(res[i] - i);
}
return res;
};直接计算距离:
JavaScript Code
/**
* @param {string} S
* @param {character} C
* @return {number[]}
*/
var shortestToChar = function (S, C) {
var res = Array(S.length);
for (let i = 0; i < S.length; i++) {
if (S[i] === C) res[i] = 0;
// 记录距离:res[i - 1] + 1
else res[i] = res[i - 1] === void 0 ? Infinity : res[i - 1] + 1;
}
for (let i = S.length - 1; i >= 0; i--) {
// 更新距离:res[i + 1] + 1
if (res[i] === Infinity || res[i + 1] + 1 < res[i]) res[i] = res[i + 1] + 1;
}
return res;
};Python Code:
class Solution:
def shortestToChar(self, S: str, C: str) -> List[int]:
pre = -len(S)
ans = []
for i in range(len(S)):
if S[i] == C: pre = i
ans.append(i - pre)
pre = len(S) * 2
for i in range(len(S) - 1, -1, -1):
if S[i] == C: pre = i
ans[i] = min(ans[i], pre - i)
return ans解法 4:窗口
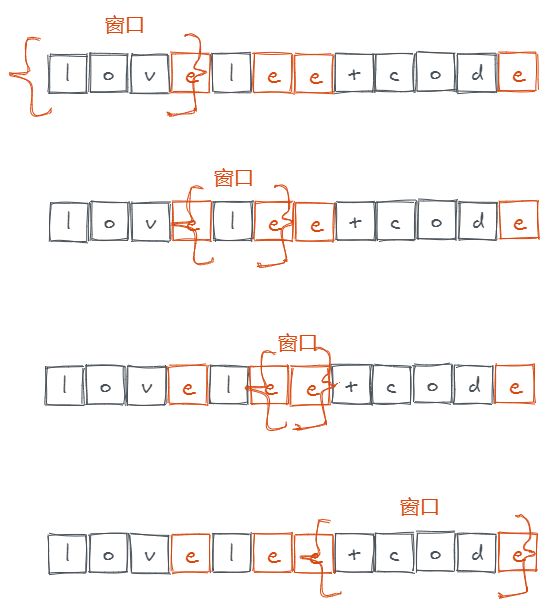
思路
把 C 看成分界线,将 S 划分成一个个窗口。然后对每个窗口进行遍历,分别计算每个字符到窗口边界的距离最小值,并在遍历的过程中更新窗口信息即可。
复杂度分析
由于更新窗口里的“搜索”下一个窗口的操作总共只需要 $N$ 次,因此时间复杂度仍然是 $N$,而不是 $N^2$。
- 时间复杂度:$O(N)$,N 是 S 的长度。
- 空间复杂度:$O(1)$。
代码
JavaScript Code
/**
* @param {string} S
* @param {character} C
* @return {number[]}
*/
var shortestToChar = function (S, C) {
// 窗口左边界,如果没有就初始化为 Infinity
let l = S[0] === C ? 0 : Infinity,
// 窗口右边界
r = S.indexOf(C, 1);
const res = Array(S.length);
for (let i = 0; i < S.length; i++) {
// 计算字符到当前窗口左右边界的最小距离
res[i] = Math.min(Math.abs(i - l), Math.abs(r - i));
// 遍历完了当前窗口的字符后,将整个窗口右移
if (i === r) {
l = r;
r = S.indexOf(C, l + 1);
}
}
return res;
};小结
本文给大家介绍了这道题的四种解法,从直觉思路入手,到使用空间换时间的策略,再到贪心算法思想,最后是一个简单直白,同时复杂度也是最优的思路。
对于刚开始做题的人来说,"做出来"是首要任务,但如果你有余力的话,也可以试试这样"一题多解",多锻炼一下自己。
但无论怎样,只要你对算法感兴趣,一定要考虑关注 lucifer 这个算法灯塔哦。不要嫌我啰嗦,真话不啰嗦。
更多题解可以访问:https://github.com/suukii/91-days-algorithm
end
大家对此有何看法,欢迎给我留言,我有时间都会一一查看回答。更多算法套路可以访问我的 LeetCode 题解仓库:https://github.com/azl3979858... 。 目前已经 37K star 啦。大家也可以关注我的公众号《力扣加加》带你啃下算法这块硬骨头。
我整理的 1000 多页的电子书已限时免费下载,大家可以去我的公众号《力扣加加》后台回复电子书获取。