前言需求
本篇算法介绍的十大常用算法的:分治算法,那么在前面的一些算法文章中就有分治算法的概念
一、什么是分治算法?
简单来说字面意思就是‘分而治之’,就是把一个复杂的问题分成两个或者更多的相同或类似的子问题,再把子问题分成更小的子问题
这种思想是很多高效算法的基础,如:快速排序、归并排序、博立叶交换等
分治法在每一层递归上都有三个步骤:
1.分解:将原问题分解为若干个规模较小,相互独立,与原问题形式相同的子问题
2.解决:若子问题规模较小而容易被解决则直接解,否则递归地解各个子问题
3.合并:将各个子问题的解合并为原问题的解。
二、分治算法的设计模式
if |P|≤n0 then return(ADHOC(P))其中|P|表示问题P的规模;n0为一阈值,表示当问题P的规模不超过n0时,问题已容易直接解出,不必再继续分解,ADHOC(P)是该分治法中的基本子算法,用于直接解小规模的问题P。
//将P分解为较小的子问题 P1 ,P2 ,…,Pk
for i←1 to k
do yi ← Divide-and-Conquer(Pi) 递归解决Pi
T ← MERGE(y1,y2,…,yk) 合并子问题
return(T)因此,当P的规模不超过n0时直接用算法ADHOC(P)求解,否则拆为其他子问题。算法MERGE(y1,y2,…,yk)是该分治法中的合并子算法,用于将P的子问题P1 ,P2 ,…,Pk的相应的解y1,y2,…,yk合并为P的解
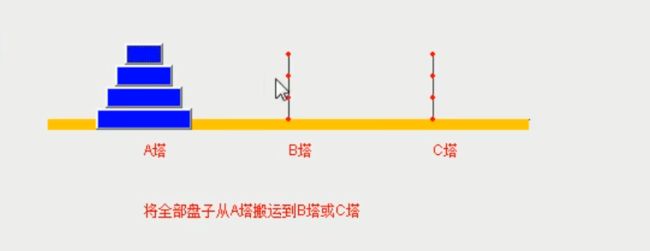
三、分治算法最佳实践-汉诺塔
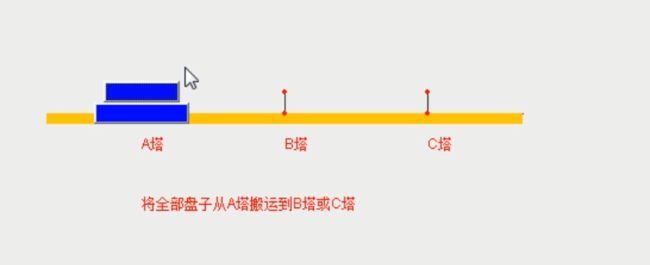
简单盘汉诺塔的演示
1.最简单的时候,只有一个盘,A、B、C塔,只需一步到位
2.复杂一点时有两个盘,A、B、C塔,会怎么操作呢?
汉诺塔思路分析
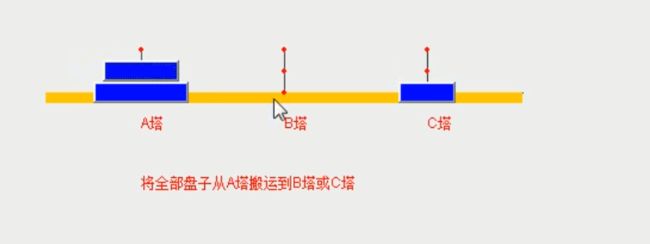
1.从两种情况来说,我们可以不管A塔有多少盘,我们都可以看成二个盘(最上、最下)
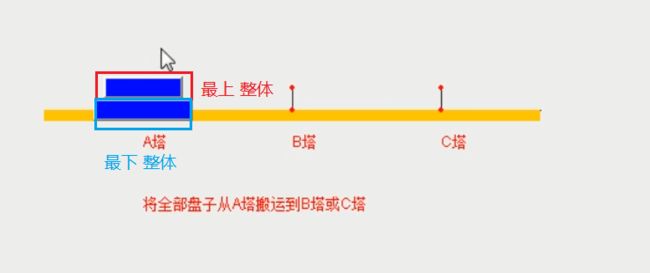
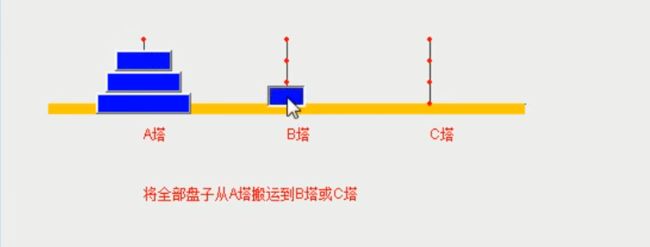
2.第一步:将最上面的盘移至B塔
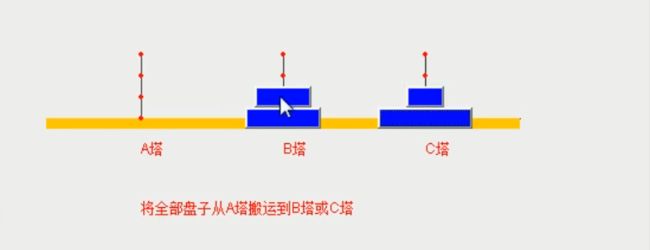
3.第二步:将最下面的盘移至C塔
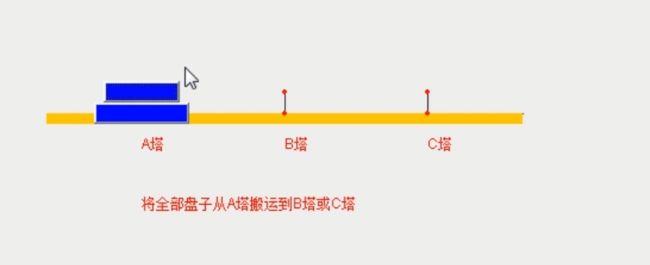
4.第三步:将B塔上的所有盘移至C塔
更多盘的汉诺塔演示
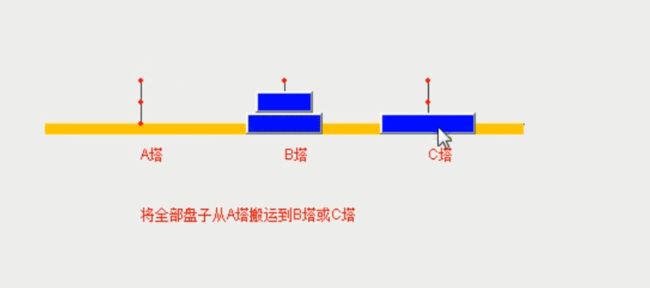
3.再复杂一点时有三个盘,A、B、C塔,会怎么操作呢?
那么根据我们的思路分析,此时我们应该是分成看做二个盘(最上、最下)
那么第一步:我们先将最上面的塔移至B塔
接下来执行第二步:将最下面的盘移至C塔
接下来第三步:将B塔上的所有盘移至C塔
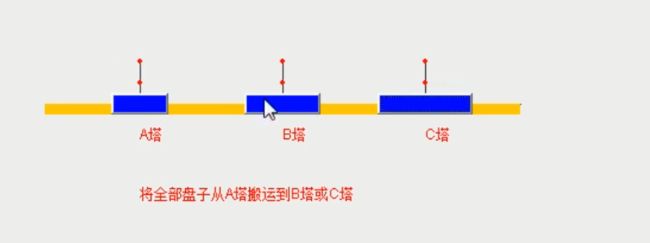
4.再复杂一点时有四个盘,A、B、C塔,会怎么操作呢?
那么根据我们的思路分析,此时我们应该是分成看做二个盘(最上、最下)
那么第一步:我们先将最上面的塔移至B塔
接下来执行第二步:将最下面的盘移至C塔
接下来第三步:将B塔上的所有盘移至C塔
汉诺塔代码思路分析
1.如果只有一个盘的时候,只需要一步到位即可
2.如果我们盘的数量n,它是 n >= 2的时候,我们看做两个盘(最上、最下)
2.1第一步:我们需要将最上面的盘移至B塔
2.2第二步:我们需要将最下面的盘移至C塔
2.3第三步:我们需要将B塔上的所有盘移至C塔
//汉诺塔移动的方法
//使用分治算法
public static void hanioTower(int num,char a ,char b,char c){
//如果只有一个盘,那么就是移动一次
if(num == 1){
System.out.println("第1个盘从 " + a + " ->" + c);
}else{
//如果我们盘的数量n,它是 n >= 2的时候,我们看做两个盘(最上、最下)
//2.1第一步:我们需要将最上面的盘移至B塔
hanioTower(num -1,a,c,b);
//2.2第二步:我们需要将最下面的盘移至C塔
System.out.println("第" + num +"个盘从 " + a +" ->"+ c);
//2.3第三步:我们需要将B塔上的所有盘移至C塔
hanioTower(num -1 ,b , a , c);
}
}我们根据不同盘数情况,使用demo 测试看看吧
public static void main(String[] args) {
//只有一个盘的情况
hanioTower(1,'a','b','c');
}
运行结果如下:
第1个盘从 a ->cpublic static void main(String[] args) {
//有二个盘的情况
hanioTower(2,'a','b','c');
}
运行结果如下:
第1个盘从 a ->b
第2个盘从 a ->c
第1个盘从 b ->cpublic static void main(String[] args) {
//有三个盘的情况
hanioTower(3,'a','b','c');
}
运行结果如下:
第1个盘从 a ->c
第2个盘从 a ->b
第1个盘从 c ->b
第3个盘从 a ->c
第1个盘从 b ->a
第2个盘从 b ->c
第1个盘从 a ->c