-----------
通知:如果本站对你学习算法有帮助,请收藏网址,并推荐给你的朋友。由于 labuladong 的算法套路太火,很多人直接拿我的 GitHub 文章去开付费专栏,价格还不便宜。我这免费写给你看,多宣传原创作者是你唯一能做的,谁也不希望劣币驱逐良币对吧?
咱们的公众号有很多硬核的算法文章,今天就聊点轻松的,就具体聊聊我非常“鼓吹”的《算法4》。这本书我在之前的文章多次推荐过,但是没有具体的介绍,今天就来正式介绍一下。。
我的推荐不会直接甩一大堆书目,而是会联系实际生活,讲一些书中有趣有用的知识,无论你最后会不会去看这本书,本文都会给你带来一些收获。
首先这本书是适合初学者的。总是有很多读者问,我只会 C 语言,能不能看《算法4》?学算法最好用什么语言?诸如此类的问题。
经常看咱们公众号的读者应该体会到了,算法其实是一种思维模式,和你用什么语言没啥关系。我们的文章也不会固定用某一种语言,而是什么语言写出来容易理解就用什么语言。再退一步说,到底适不适合你,网上找个 PDF 亲自看一下不就知道了?
《算法4》看起来挺厚的,但是前面几十页是教你 Java 的;每章后面还有习题,占了不少页数;每章还有一些数学证明,这些都可以忽略。这样算下来,剩下的就是基础知识和疑难解答之类的内容,含金量很高,把这些基础知识动手实践一遍,真的就可以达到不错的水平了。
我觉得这本书之所以能有这么高的评分,一个是因为讲解详细,还有大量配图,另一个原因就是书中把一些算法和现实生活中的使用场景联系起来,你不仅知道某个算法怎么实现,也知道它大概能运用到什么场景,下面我就来介绍两个图算法的简单应用。
一、二分图的应用
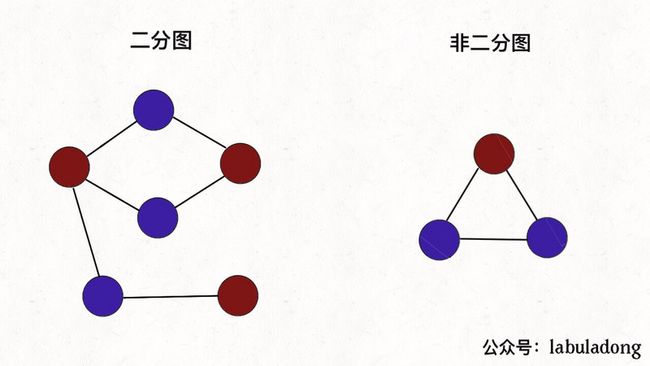
我想举的第一个例子是二分图。简单来说,二分图就是一幅拥有特殊性质的图:能够用两种颜色为所有顶点着色,使得任何一条边的两个顶点颜色不同。
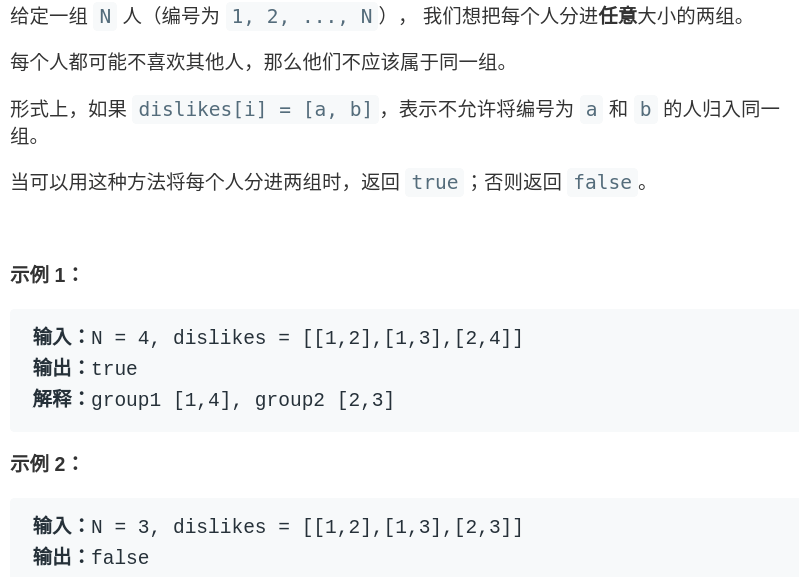
明白了二分图是什么,能解决什么实际问题呢?算法方面,常见的操作是如何判定一幅图是不是二分图。比如说下面这道 LeetCode 题目:
你想想,如果我们把每个人视为一个顶点,边代表讨厌;相互讨厌的两个人之间连接一条边,就可以形成一幅图。那么根据刚才二分图的定义,如果这幅图是一幅二分图,就说明这些人可以被分为两组,否则的话就不行。
这是判定二分图算法的一个应用,其实二分图在数据结构方面也有一些不错的特性。
比如说我们需要一种数据结构来储存电影和演员之间的关系:某一部电影肯定是由多位演员出演的,且某一位演员可能会出演多部电影。你使用什么数据结构来存储这种关系呢?
既然是存储映射关系,最简单的不就是使用哈希表嘛,我们可以使用一个 HashMap 来存储电影到演员列表的映射,如果给一部电影的名字,就能快速得到出演该电影的演员。
但是如果给出一个演员的名字,我们想快速得到该演员演出的所有电影,怎么办呢?这就需要「反向索引」,对之前的哈希表进行一些操作,新建另一个哈希表,把演员作为键,把电影列表作为值。
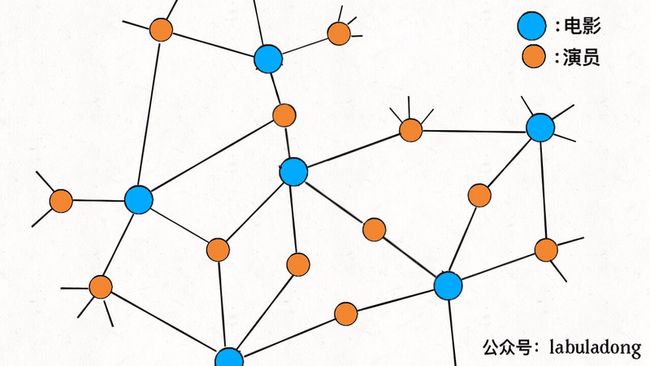
对于上面这个例子,可以使用二分图来取代哈希表。电影和演员是具有二分图性质的:如果把电影和演员视为图中的顶点,出演关系作为边,那么与电影顶点相连的一定是演员,与演员相邻的一定是电影,不存在演员和演员相连,电影和电影相连的情况。
回顾二分图的定义,如果对演员和电影顶点着色,肯定就是一幅二分图:
如果这幅图构建完成,就不需要反向索引,对于演员顶点,其直接连接的顶点就是他出演的电影,对于电影顶点,其直接连接的顶点就是出演演员。
当然,对于这个问题,书中还提到了一些其他有趣的玩法,比如说社交网络中「间隔度数」的计算(六度空间理论应该听说过)等等,其实就是一个 BFS 广度优先搜索寻找最短路径的问题,具体代码实现这里就不展开了。
二、套汇的算法
如果我们说货币 A 到货币 B 的汇率是 10,意思就是 1 单位的货币 A 可以换 10 单位货币 B。如果我们把每种货币视为一幅图的顶点,货币之间的汇率视为加权有向边,那么整个汇率市场就是一幅「完全加权有向图」。
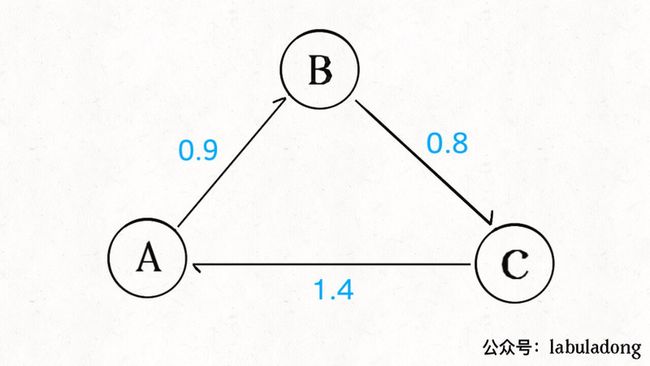
一旦把现实生活中的情景抽象成图,就有可能运用算法解决一些问题。比如说图中可能存在下面的情况:
图中的加权有向边代表汇率,我们可以发现如果把 100 单位的货币 A 换成 B,再换成 C,最后换回 A,就可以得到 100×0.9×0.8×1.4 = 100.8 单位的 A!如果交易的金额大一些的话,赚的钱是很可观的,这种空手套白狼的操作就是套汇。
现实中交易会有种种限制,而且市场瞬息万变,但是套汇的利润还是很高的,关键就在于如何快速找到这种套汇机会呢?
借助图的抽象,我们发现套汇机会其实就是一个环,且这个环上的权重之积大于 1,只要在顺着这个环交易一圈就能空手套白狼。
图论中有一个经典算法叫做 Bellman-Ford 算法,可以用于寻找负权重环。对于我们说的套汇问题,可以先把所有边的权重 w 替换成 -ln(w),这样「寻找权重乘积大于 1 的环」就转化成了「寻找权重和小于 0 的环」,就可以使用 Bellman-Ford 算法在 O(EV) 的时间内寻找负权重环,也就是寻找套汇机会。
《算法4》就介绍到这里,关于上面两个例子的具体内容,可以自己去看书,公众号后台回复关键词「算法4」就有 PDF。
三、最后说几句
首先,前文说对于数学证明、章后习题可以忽略,可能有人要抬杠了:难道习题和数学证明不重要吗?
那我想说,就是不重要,起码对大多数人来说不重要。我觉得吧,学习就要带着目的性去学,大部分人学算法不就是巩固计算机知识,对付面试题目吗?如果是这个目的,那就学些基本的数据结构和经典算法,明白它们的时间复杂度,然后去刷题就好了,何必和习题、证明过不去?
这也是我从来不推荐《算法导论》这本书的原因。如果有人给你推荐这本书,只可能有两个原因,要么他是真大佬,要么他在装大佬。《算法导论》中充斥大量数学证明,而且很多数据结构是很少用到的,顶多当个字典用。你说你学了那些有啥用呢,饶过自己呗。
另外,读书在精不在多。你花时间《算法4》过个大半(最后小半部分有点困难),同时刷点题,看看咱们的公众号文章,算法这块真就够了,别对细节问题太较真。