前言
此文根据左老师课程和自己理解整理成该篇文章。写的比较详细,所以文章较长,请耐心看完。
问题引入
本文先不给出线段树的定义,先来看一个问题,从而了解线段树这个数据结构是干嘛的。
假设现在有一个数组arr,长度为n,希望可以提供三个接口来完成用户的需求。
第一个接口是void add(int L,int R,int v) ,该接口表示的含义是在arr数组的[L,R]范围上的每一个数字都加上v。
第二个接口是void update(int L,int R,int v),该接口表示的含义是在arr数组的[L,R]范围上的每一个数字都变成v。
第三个接口是int getSum(int L,int R),该接口表示的含义是返回arr数组的[L,R]范围上的累加和。我们先来看看朴素求解法是怎么做到的。
public void update(int L, int R, int C) {
for (int i = L; i <= R; i++) {
arr[i] = C;
}
}
public void add(int L, int R, int C) {
for (int i = L; i <= R; i++) {
arr[i] += C;
}
}
public long getSum(int L, int R) {
long ans = 0;
for (int i = L; i <= R; i++) {
ans += arr[i];
}
return ans;
}显而易见,朴素求解法的时间复杂度为$O(n)$,那么线段树其实也是做得相同的事情,只不过其时间复杂度降低到了$O(logn)$。
定义
线段树是用来存放给定区间内对应信息的一种数据结构。在此基础上,它提供的区间元素的查询,修改和更新操作。并且所有操作的时间复杂度为$O(logn)$.
基本实现
线段树为什么可以在O(logn)的时间内进行查询和修改操作呢?
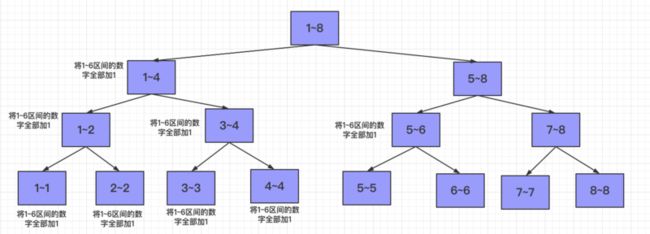
根据logn和树这两个信息就可以大概知道它的操作过程和树基本一致,线段树实际上是采用了分而治之的思想来处理区间信息,举个例子就知道了。现在假设arr的长度为8,那么初始区间范围为[1,8] (起点从1开始),那么初始我们使用一个节点来存储[1,8]的总和。然后我们进行二分后就得到了区间[1,4]和[5,8]分别作为[1,8]的左右孩子,同样的这两个区间也记录了自己的区间总和,依次类推得到下图
那么该树的叶子节点保存的就是arr数组的信息,对于每一个非叶节点只要获取左右孩子的信息后就可以获得当前节点的信息。同时对于只要在根节点范围内的信息都可以由该树所生成。
比如要获得区间[1,5]的部分和信息就可以通过获得[1,4]和[5,5]的信息来获得,而[1,4]只要获得[1,2]和[3,4]的信息进行累加即可,对于[1,2]和[3,4]亦是如此。并且可以证明只要是[1,8]的子区间的信息一定可以通过该树获得。
Q:为什么下标从1开始而不是从0开始?
A:因为从1开始就可以通过数组来保存一个满二叉树的信息了,对于任意节点i的左孩子为2i,右孩子为2i+1。
Q:线段树的长度一定是$2^n$吗?
A:不一定,对于$2^n$长度的数组,其构成的线段树没有任何冗余信息,但是对于不是$2^n$长度的数组我们需要将其扩展,保证从底层构建起来的二叉树是一颗满二叉树,对于不存在的节点,我们将其区间和置为0即可。
Q:存储线段树的数组得开多大?
A:arr的数组长度为n的话,存储线段树的数组得开到4n。
Q:为什么数组得开到4n?
A:假设数组长度为n,并且n可以写成$2^m$的形式,那么其构建出来的满二叉树的节点个数为2n-1(叶子节点n个,非叶节点n-1个),这是最为理想的情况,现在考虑最坏的情况,如果此时数组长度为n+1,就说明对于构建的满二叉树恰好多出来一个节点,为了保证构建出来的二叉树是满二叉树,我们需要人为添加一些区间和为0的节点保证构建起来的二叉树为满二叉树。对于多出来的1个节点,需要添加n-1个叶子节点来构造满二叉树(实际就是保证叶子节点的个数为2的m次幂),也就是说,此时的叶子节点为2n个,非叶节点为2n-1个,也就是存储该树需要4n-1的容量,所以需要将数组开到4n。画个图看的更加直观。
Q:线段树的结构是否一定需要是满二叉树?
A:是的,因为为了保证每一次二分区间均等,需要将其构建为满二叉树。
线段树的构建过程
从上面线段树的基本实现上可以知道,我们只需要构建树中的非叶节点,而每一个非叶节点都是通过左右孩子的信息累加所获得的,这恰好满足二叉树后序遍历的定义,那么我们可以使用后序递归遍历的方法进行建树。
假设现在初始数组为origin,下标从0开始,长度为n,构建二叉树之前需要将其拷贝到arr数组中,使其下标从1开始,然后我们使用sum数组保存树中每一个节点代表的区间和信息,比如$sum[1]$代表了arr数组中$[1,n]$的部分和,$sum[2]$代表了arr数组中$[1,n/2]$的部分和。构建过程如下图所示。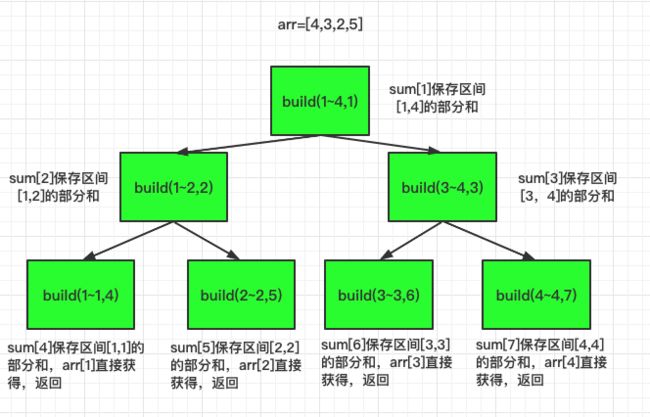
上图表示的调用build的递归过程。其代码实现如下:
public static class SegmentTree {
// arr[]为原序列的信息从0开始,但在arr里是从1开始的
// sum[]模拟线段树维护区间和
// lazy[]为累加懒惰标记
private int MAXN;
private int[] arr;
private int[] sum;
public SegmentTree(int[] origin) {
MAXN = origin.length + 1;
arr = new int[MAXN]; // arr[0] 不用 从1开始使用
for (int i = 1; i < MAXN; i++) {
arr[i] = origin[i - 1];
}
sum = new int[MAXN << 2]; // 用来支持脑补概念中,某一个范围的累加和信息
}
private void pushUp(int rt) {
sum[rt] = sum[rt << 1] + sum[rt << 1 | 1];
}
// 在初始化阶段,先把sum数组,填好
// 在arr[l~r]范围上,去build,1~N,
// rt : 这个范围在sum中的下标
public void build(int l, int r, int rt) {
if (l == r) {
sum[rt] = arr[l];
return;
}
int mid = (l + r) >> 1;
build(l, mid, rt << 1);
build(mid + 1, r, rt << 1 | 1);
pushUp(rt);
}
}
线段树的添加操作:将[L,R]区间上的每一个元素都添加数值v
假设现在arr的区间为[1,8],而我们希望在区间[1,6]上添加一个1,那么会发生什么?
1~6无法覆盖1~8区间,所以根节点不能直接在1~8上全部加1,1~6和1~8的左右孩子都有交集,将其任务下发到左右孩子。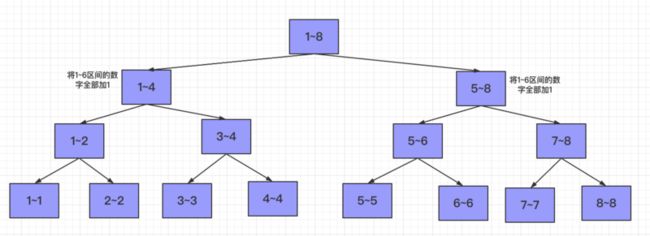
先看左边1~4区间恰好可以完全被1~6覆盖,所以以1~4为根节点的子树的所有节点的区间和都得加$1*区间大小$,而对于右边5~8没有被1~6完全覆盖,同样不能直接在该区间将所有元素加1,得下发给左孩子进行处理(右孩子没有交集)。
对于5~6区间恰好可以被1~6覆盖,说明以5~6为根节点的子树的所有节点的区间和都需要加上$1*区间大小$。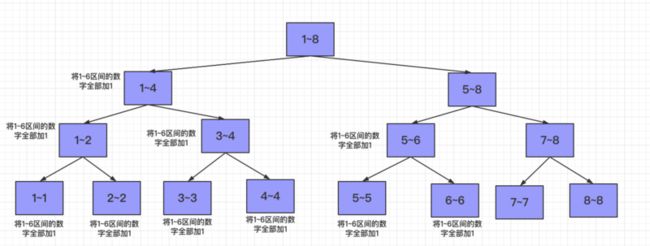
这样每一个节点更新完毕后,就往上返回更新的值,从而更新非叶节点存储的区间部分和。
我们仔细看看该过程存在哪些问题,每一次对某一个区间上的元素加v的操作都会传递到叶子节点,但其实完全可以没有必要这么做,因为数据的更新过程往往是为了数据的查询过程来服务的,如果我们只有需要查询某一个区间的信息的时候再往下更新更小子区间的信息,这样就做到了更新操作的剪枝,也叫做懒更新。
比如对区间$[1,6]$的所有元素都加1的过程中,实际上,对于$[1,4]$区间就没有必要往下再传递该任务,因为1~6完全覆盖了1~4区间,我们就只需要更新1~4区间的部分和就可以提供最新的1~8的左子区间的部分和了,只有在确切需要知道1~4的子节点的区间部分和的时候再将该任务往下传递就好。
这样做的好处在于,可以将多次add操作压缩为一次add操作,如果后面还有将1~5区间的每一个元素加2的任务,那么1~4就会累计1~4区间每一个元素加3的任务,在需要获得1~2的任务的时候,直接将1~2的每一个元素加3就可以获得最小的信息,而不是先加1,再加2。
具体的做法就是使用一个lazy数组存储每一个节点堆积的add任务,比如lazy[1]代表的就是1~8上堆积的add任务(具体加多少),lazy初始为0。
Q:那么什么时候会产生这个任务呢?
A:当需要执行add任务的区间[L,R]完全覆盖当前节点的区间的时候就在当前节点的lazy数组上累计。比如在1~4上会累计在1~6上每一个元素加1的任务,那么lazy[2] += 1;5~6区间也是如此,lazy[6] += 1;
Q:什么时候无法进行懒更新,需要将任务往下发呢?
A:当需要执行的任务的区间[L,R]无法完全覆盖当前节点的区间的时候,就需要将当前节点上累计的lazy任务全部往下发,更新子节点的数据,知道再次出现完全覆盖子节点区间即可。这里的任务可以是添加也可以是查询。
对于在区间[L,R]上的每一个元素添加v的操作流程总结如下:
1)如果当前任务区间[L,R]可以完全覆盖当前节点所表示的区间[l,r],那么可以进行懒更新,累计sum和lazy数组,然后返回。否则转2)
2)先下发之前积累的lazy任务给自己的左右孩子,具体做法就是将该lazy任务累加到左右孩子的lazy任务上并且更新左右孩子的sum数组为lazy数值*左右孩子区间的长度。
3)如果[L,R]和左孩子区间有交集,将该任务下发到左孩子
4)如果[L,R]和右孩子区间有交集,将该任务下发到右孩子
5)左右孩子处理完毕后,更新当前节点区间和的信息。实现代码如下:
// ln表示左子树元素结点个数,rn表示右子树结点个数
private void pushDown(int rt, int ln, int rn) {
if (lazy[rt] != 0) {
lazy[rt << 1] += lazy[rt];
sum[rt << 1] += lazy[rt] * ln;
lazy[rt << 1 | 1] += lazy[rt];
sum[rt << 1 | 1] += lazy[rt] * rn;
lazy[rt] = 0;
}
}
// L..R -> 任务范围 ,所有的值累加上V
// l,r -> 表达的范围
// rt 去哪找l,r范围上的信息
public void add(
int L, int R, int V,
int l, int r,
int rt) {
// 任务的范围彻底覆盖了,当前表达的范围
if (L <= l && r <= R) {
sum[rt] += V * (r - l + 1);
lazy[rt] += V;
return;
}
// 要把当前任务往下发
// 任务 L, R 没有把本身表达范围 l,r 彻底包住
int mid = (l + r) >> 1; // l..mid (rt << 1) mid+1...r(rt << 1 | 1)
// 下发之前所有攒的懒任务
pushDown(rt, mid - l + 1, r - mid);
// 左孩子是否需要接到任务
if (L <= mid) {
add(L, R, V, l, mid, rt << 1);
}
// 右孩子是否需要接到任务
if (R > mid) {
add(L, R, V, mid + 1, r, rt << 1 | 1);
}
// 左右孩子做完任务后,我更新我的sum信息
pushUp(rt);
}
线段树的更新操作:将区间[L,R]上的每一个元素都置为v
首先得明确一点,如果当前节点接受到一个更新每一个元素为v的任务,那么在当前节点上累计的lazy任务一定会被丢弃,也就是置为0,因为没有必要进行累计了,每一个元素一定变为v。
在讲述其过程的之前,先引入两个数组,一个为update数组,表示当前节点是否有积累的更新任务,另外一个为change数组,表示当前节点积累的更新数字是多少。只有在update[i]为true的时候,才会使用到change数组,两者需要搭配使用。
接下来通过一个理解演示如何进行add和update操作(混合进行),假设数组初始全部为0,区间范围为[1,8],那么sum数组自然也全部为0,方便计算。
第一个任务:将[1,4]范围内的每一个数字都加2。
那么只有1~4节点更新$sum += 2*4,lazy += 2$。然后更新父节点1~8的sum为左右孩子节点sum之和。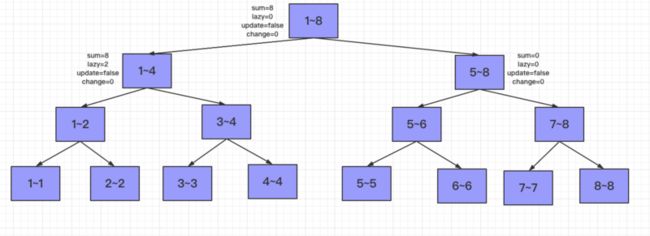
第二个任务:将[5,8]范围内的每一个数字都加1。
那么只有5~8节点更新$sum += 1*4,lazy += 1$。然后更新父节点1~8的sum为左右孩子节点sum之和。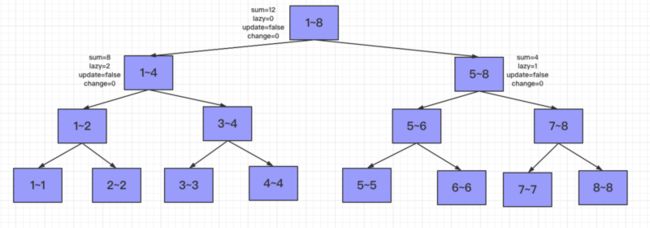
第三个任务:将[1,8]范围内的数字都更新为2.
那么只有1~8节点的$update=true,change=2$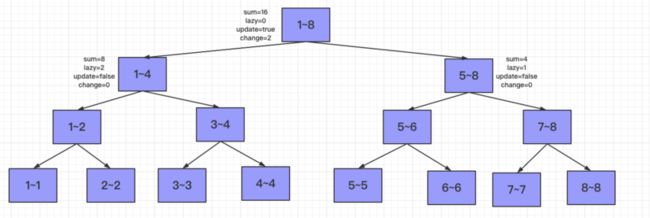
第四个任务:将[1,8]范围内的数字都增加3.
那么只有1~8节点的$sum += 3*8,lazy += 3$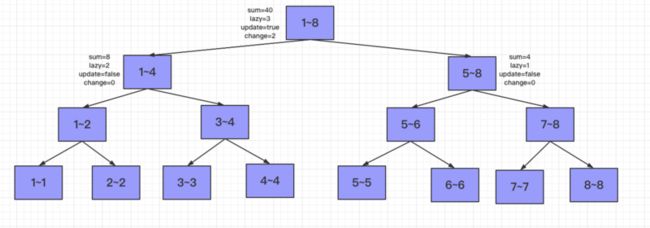
第五个任务:将[1,6]范围的数字都增加1
由于1~8无法被1~6覆盖,所以需要将该任务下发给自己的孩子节点,但是此时当前节点有懒更新操作,所以需要先将懒更新任务发下去,首先是将update任务进行下发,先将左孩子1~4和右孩子5~8的sum,lazy全部置为0,然后update置为true,change更改为当前节点的change(值为2)。然后将当前节点的update置为false,change置为0.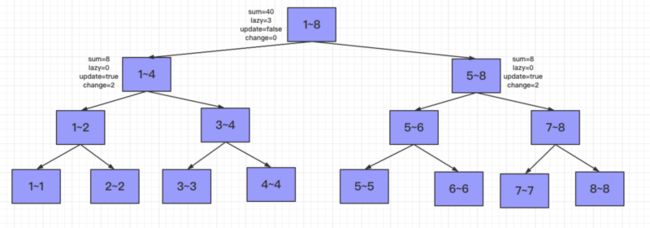
接下来得分发lazy任务,左右孩子的$sum += 3*4(当前节点lazy值*孩子节点区间长度),lazy += 3$,然后将当前节点的lazy置为0.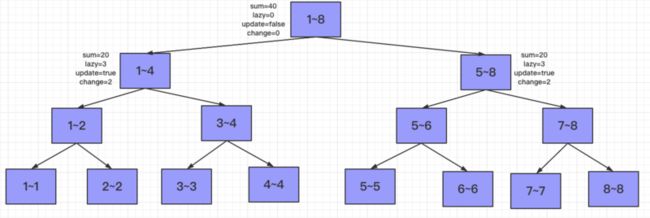
最后得分发在1~6的元素都添加1的任务了,由于和左右区间都有交集,所以分发给左右孩子节点,左节点1~4可以被1~6覆盖,所以进行懒更新,$lazy += 1,sum += 1*4$,右节点无法完全覆盖,并且5~8节点还有自己累积的懒更新操作,同样的需要先下发update任务,再下发lazy任务。5~8节点的左右孩子同时更新$update=true,change=2,sum+=2*2+3*2,lazy+=3$。并将5~8节点的$update$置为$false,change=0,lazy=0$。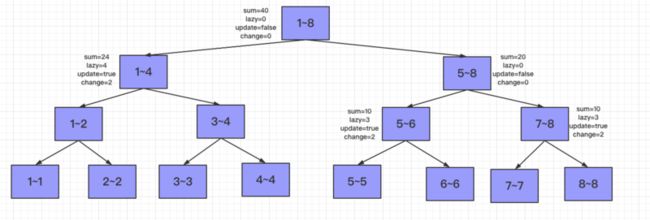
接下来就可以分发1~6的元素都添加1的任务给5~6节点了(7~8没有交集),将5~6节点可以被1~6完全覆盖,所以将$sum+=2*1,lazy+=1。$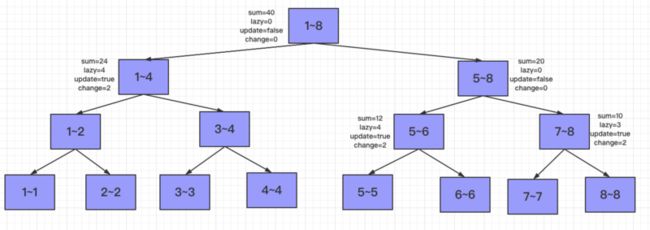
最后得将更新的结果向上汇总,首先是5~6和7~8的总和22作为5~8的新的sum,然后1~4和5~8的总和46作为1~8新的sum。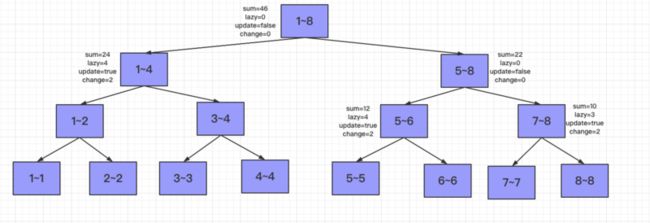
从上述例子中,我们发现在往下发懒更新任务的时候,会同时存在update任务和add任务的情形,这种情况下,先下发update,然后再下发add任务。
update任务下发过程总结如下:
1)将当前节点的update和change数值赋值给左右孩子的update和change
2)左右孩子的lazy数字全部为0
3)左右孩子的sum数字累加change数值*左右孩子区间长度
4)当前节点的update置为false,change置为0(可以不要,因为有新的更新操作懒更新的时候会直接覆盖)
lazy任务下发过程总结如下
1)将左右孩子的lazy数值累加当前节点的lazy数值
2)将左右孩子的sum数字累加lazy数值*左右孩子区间长度
3)当前节点的lazy数值置为0.其代码实现如下:
// 之前的,所有懒增加,和懒更新,从父范围,发给左右两个子范围
// 分发策略是什么
// ln表示左子树元素结点个数,rn表示右子树结点个数
private void pushDown(int rt, int ln, int rn) {
if (update[rt]) {
update[rt << 1] = true;
update[rt << 1 | 1] = true;
change[rt << 1] = change[rt];
change[rt << 1 | 1] = change[rt];
lazy[rt << 1] = 0;
lazy[rt << 1 | 1] = 0;
sum[rt << 1] = change[rt] * ln;
sum[rt << 1 | 1] = change[rt] * rn;
update[rt] = false;
}
if (lazy[rt] != 0) {
lazy[rt << 1] += lazy[rt];
sum[rt << 1] += lazy[rt] * ln;
lazy[rt << 1 | 1] += lazy[rt];
sum[rt << 1 | 1] += lazy[rt] * rn;
lazy[rt] = 0;
}
}更新操作与添加操作不同的地方在于当前节点区间被覆盖的时候需要更新update和change数组,sum和lazy不在是累计而是直接赋值操作。
更新操作流程总结如下:
1)如果当前节点所表示的区间可以被更新任务区间[L,R]覆盖,那么直接更新update=true,change=更新值,sum+=更新值*节点区间长度,lazy=0,并返回。
2)如果没有办法覆盖,先将累计的懒加载操作进行下发,下发该更新任务给左右孩子。
3)如果左孩子代表区间与[L,R]有交集,下发任务到左孩子。
4)如果右孩子代表区间与[L,R]有交集,下发任务到右孩子。
5)最后更新当前节点区间部分和。其实现代码如下:
public SegmentTree(int[] origin) {
MAXN = origin.length + 1;
arr = new int[MAXN]; // arr[0] 不用 从1开始使用
for (int i = 1; i < MAXN; i++) {
arr[i] = origin[i - 1];
}
sum = new int[MAXN << 2]; // 用来支持脑补概念中,某一个范围的累加和信息
lazy = new int[MAXN << 2]; // 用来支持脑补概念中,某一个范围沒有往下傳遞的纍加任務
change = new int[MAXN << 2]; // 用来支持脑补概念中,某一个范围有没有更新操作的任务
update = new boolean[MAXN << 2]; // 用来支持脑补概念中,某一个范围更新任务,更新成了什么
}public void update(int L, int R, int C, int l, int r, int rt) {
if (L <= l && r <= R) {
update[rt] = true;
change[rt] = C;
sum[rt] = C * (r - l + 1);
lazy[rt] = 0;
return;
}
// 当前任务躲不掉,无法懒更新,要往下发
int mid = (l + r) >> 1;
pushDown(rt, mid - l + 1, r - mid);
if (L <= mid) {
update(L, R, C, l, mid, rt << 1);
}
if (R > mid) {
update(L, R, C, mid + 1, r, rt << 1 | 1);
}
pushUp(rt);
}线段树查询:查询[L,R]区间上的部分和
假设现在的线段树状态如上面的例子所示,虽然已经完成了更新操作,但是依然存在懒更新操作没有往下发。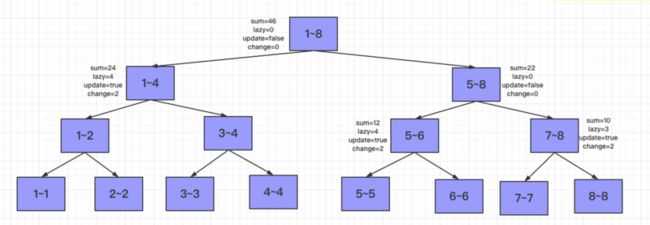
我们现在需要查询[3,5]区间的部分和,那么1~8范围无法被3~5覆盖,并且没有懒更新操作积累,所以可以直接将该任务下发给左右孩子节点。
先来看左孩子1~4,当前节点所表示的范围依然无法被3~5覆盖,并且有懒更新操作积累,需要先进行懒更新操作下发,先将update任务下发,左右孩子的$update=true,change=2,sum += 2*2$,然后再将lazy任务下发,左右孩子的$lazy += 4,sum += 2*2+2*4$。并更新1~4节点的$lazy=0,update=false,change=0$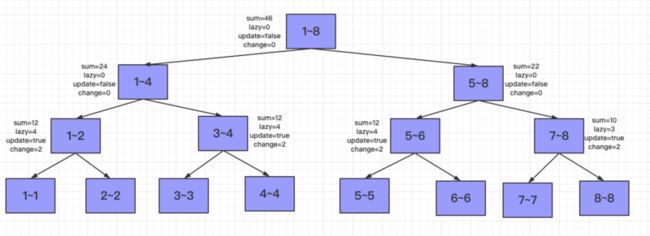
然后下发3~5查询任务到右孩子3~4,3~4可以被3~5完全覆盖,直接返回查询结果12。
现在来看右节点5~8,5~8依然不能被3~5覆盖,但是没有积累懒更新操作,所以可以直接下发给左孩子(7~8没有交集)。来到5~6之后,发现5~6也无法被3~5覆盖,但是5~6节点积累了懒更新操作,所以需要先将update操作下发,左右孩子的$sum+=2*1,update=true,change=2$,然后将lazy任务往下发,左右孩子节点的$sum+=2*1+4*1,lazy+=4$。并更新5~6节点的$lazy=0,update=false,change=0$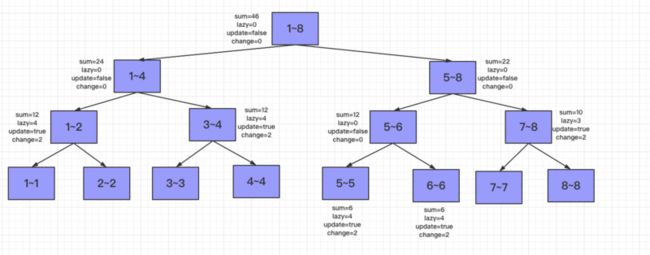
然后再将查询3~5区间和任务往左孩子发送,直接来到5~5节点可以被3~5覆盖,返回结果6.这样得到区间[3,5]的部分和6+12=18.
查询[L,R]部分和操作流程总结:
1)如果当前节点所表示区间可以被[L,R]覆盖,直接返回结果。否则转2)
2)如果当前节点存在懒更新任务,先下发懒更新任务,然后下发查询任务。
3)如果左区间和查询区间有交集,累计左区间部分和
4)如果右区间和查询区间有交集,累计右区间部分和
5)返回左右区间累计和。实现代码如下:
public long getSum(int L, int R, int l, int r, int rt) {
if (L <= l && r <= R) {
return sum[rt];
}
int mid = (l + r) >> 1;
pushDown(rt, mid - l + 1, r - mid);
long ans = 0;
if (L <= mid) {
ans += getSum(L, R, l, mid, rt << 1);
}
if (R > mid) {
ans += getSum(L, R, mid + 1, r, rt << 1 | 1);
}
return ans;
}线段树查询,添加和更新完整代码
public static class SegmentTree {
// arr[]为原序列的信息从0开始,但在arr里是从1开始的
// sum[]模拟线段树维护区间和
// lazy[]为累加懒惰标记
// change[]为更新的值
// update[]为更新慵懒标记
private int MAXN;
private int[] arr;
private int[] sum;
private int[] lazy;
private int[] change;
private boolean[] update;
public SegmentTree(int[] origin) {
MAXN = origin.length + 1;
arr = new int[MAXN]; // arr[0] 不用 从1开始使用
for (int i = 1; i < MAXN; i++) {
arr[i] = origin[i - 1];
}
sum = new int[MAXN << 2]; // 用来支持脑补概念中,某一个范围的累加和信息
lazy = new int[MAXN << 2]; // 用来支持脑补概念中,某一个范围沒有往下傳遞的纍加任務
change = new int[MAXN << 2]; // 用来支持脑补概念中,某一个范围有没有更新操作的任务
update = new boolean[MAXN << 2]; // 用来支持脑补概念中,某一个范围更新任务,更新成了什么
}
private void pushUp(int rt) {
sum[rt] = sum[rt << 1] + sum[rt << 1 | 1];
}
// 之前的,所有懒增加,和懒更新,从父范围,发给左右两个子范围
// 分发策略是什么
// ln表示左子树元素结点个数,rn表示右子树结点个数
private void pushDown(int rt, int ln, int rn) {
if (update[rt]) {
update[rt << 1] = true;
update[rt << 1 | 1] = true;
change[rt << 1] = change[rt];
change[rt << 1 | 1] = change[rt];
lazy[rt << 1] = 0;
lazy[rt << 1 | 1] = 0;
sum[rt << 1] = change[rt] * ln;
sum[rt << 1 | 1] = change[rt] * rn;
update[rt] = false;
}
if (lazy[rt] != 0) {
lazy[rt << 1] += lazy[rt];
sum[rt << 1] += lazy[rt] * ln;
lazy[rt << 1 | 1] += lazy[rt];
sum[rt << 1 | 1] += lazy[rt] * rn;
lazy[rt] = 0;
}
}
// 在初始化阶段,先把sum数组,填好
// 在arr[l~r]范围上,去build,1~N,
// rt : 这个范围在sum中的下标
public void build(int l, int r, int rt) {
if (l == r) {
sum[rt] = arr[l];
return;
}
int mid = (l + r) >> 1;
build(l, mid, rt << 1);
build(mid + 1, r, rt << 1 | 1);
pushUp(rt);
}
public void update(int L, int R, int C, int l, int r, int rt) {
if (L <= l && r <= R) {
update[rt] = true;
change[rt] = C;
sum[rt] = C * (r - l + 1);
lazy[rt] = 0;
return;
}
// 当前任务躲不掉,无法懒更新,要往下发
int mid = (l + r) >> 1;
pushDown(rt, mid - l + 1, r - mid);
if (L <= mid) {
update(L, R, C, l, mid, rt << 1);
}
if (R > mid) {
update(L, R, C, mid + 1, r, rt << 1 | 1);
}
pushUp(rt);
}
// L..R -> 任务范围 ,所有的值累加上C
// l,r -> 表达的范围
// rt 去哪找l,r范围上的信息
public void add(
int L, int R, int C,
int l, int r,
int rt) {
// 任务的范围彻底覆盖了,当前表达的范围
if (L <= l && r <= R) {
sum[rt] += C * (r - l + 1);
lazy[rt] += C;
return;
}
// 任务并没有把l...r全包住
// 要把当前任务往下发
// 任务 L, R 没有把本身表达范围 l,r 彻底包住
int mid = (l + r) >> 1; // l..mid (rt << 1) mid+1...r(rt << 1 | 1)
// 下发之前所有攒的懒任务
pushDown(rt, mid - l + 1, r - mid);
// 左孩子是否需要接到任务
if (L <= mid) {
add(L, R, C, l, mid, rt << 1);
}
// 右孩子是否需要接到任务
if (R > mid) {
add(L, R, C, mid + 1, r, rt << 1 | 1);
}
// 左右孩子做完任务后,我更新我的sum信息
pushUp(rt);
}
// 1~6 累加和是多少? 1~8 rt
public long getSum(int L, int R, int l, int r, int rt) {
if (L <= l && r <= R) {
return sum[rt];
}
int mid = (l + r) >> 1;
pushDown(rt, mid - l + 1, r - mid);
long ans = 0;
if (L <= mid) {
ans += getSum(L, R, l, mid, rt << 1);
}
if (R > mid) {
ans += getSum(L, R, mid + 1, r, rt << 1 | 1);
}
return ans;
}
}线段树应用
用Leetcode 699题 掉落的方块作为例子进行说明线段树如何使用。
在无限长的数轴(即 x 轴)上,我们根据给定的顺序放置对应的正方形方块。
第 i 个掉落的方块(positions[i] = (left, side_length))是正方形,其中 left 表示该方块最左边的点位置(positions[i][0]),side_length表示该方块的边长(positions[i][1])。
每个方块的底部边缘平行于数轴(即 x 轴),并且从一个比目前所有的落地方块更高的高度掉落而下。在上一个方块结束掉落,并保持静止后,才开始掉落新方块。
方块的底边具有非常大的粘性,并将保持固定在它们所接触的任何长度表面上(无论是数轴还是其他方块)。邻接掉落的边不会过早地粘合在一起,因为只有底边才具有粘性。
返回一个堆叠高度列表 ans 。每一个堆叠高度 ans[i] 表示在通过 positions[0], positions[1], ..., positions[i] 表示的方块掉落结束后,目前所有已经落稳的方块堆叠的最高高度。
示例 1:
输入: [[1, 2], [2, 3], [6, 1]]
输出: [2, 5, 5]
解释:
第一个方块 positions[0] = [1, 2] 掉落:
_aa
_aa
-------
方块最大高度为 2 。
第二个方块 positions[1] = [2, 3] 掉落:
__aaa
__aaa
__aaa
_aa__
_aa__
--------------
方块最大高度为5。
大的方块保持在较小的方块的顶部,不论它的重心在哪里,因为方块的底部边缘有非常大的粘性。
第三个方块 positions[1] = [6, 1] 掉落:
__aaa
__aaa
__aaa
_aa
_aa___a
--------------
方块最大高度为5。
因此,我们返回结果[2, 5, 5]。题目解释:position二维数组中保存了一堆掉落的方块,每一个方块为一个长度为2的数组,第一个为x轴下标,第二个为方块的长度,现在需要给出每一个方块下落后,x轴上的最高高度,并将结果防止数组中,最后返回。
此题就可以使用线段树来解决,因为该题只需要每一次更新方块掉落后的最大高度和查询最大高度两个操作,并且对于一个大范围的最大高度一定是两个子范围的最大高度的最大值。
首先得注意到数据范围,position中方块掉落的位置可以达到$10^8$,而个数才1000个,如果直接使用x轴坐标表示区间会出现溢出的情况,我们可以采用离散化的处理,具体来说就是先对方块按照x的起始位置进行排序,然后再给每一个方块掉落在x的起始位置和终止位置标号,这样的话,最差的情况只需要2000个标号就可以完成所有的方块形成的区间表示。之所以可以这么做的原因,是因为无论方块掉落的顺序如何,最终方块的x轴上的相对位置不会发生变化。
离散化代码如下:
public HashMap index(int[][] positions) {
TreeSet pos = new TreeSet<>();
for (int[] arr : positions) {
pos.add(arr[0]);
pos.add(arr[0] + arr[1] - 1);
}
HashMap map = new HashMap<>();
int count = 0;
for (Integer index : pos) {
map.put(index, ++count);
}
return map;
} 返回的map的大小就是方块占用下标的个数,同时也是区间的最大值N。
然后我们就开始模拟方块掉落的过程,遍历每一个方块的左右边界在map中的编号L和R,然后在[1,N]中查询[L,R]上的最大高度,在其基础上加上当前方块的高度就是[L,R]的最新高度height,然后使用max作为全局最高高度进行更新,并添加到返回集合res中,最后在更新[L,R]上高度为height即可。
主体代码如下:
public List fallingSquares(int[][] positions) {
HashMap map = index(positions);
// 100 -> 1 306 -> 2 403 -> 3
// [100,403] 1~3
int N = map.size(); // 1 ~ N
SegmentTree segmentTree = new SegmentTree(N);
int max = 0;
List res = new ArrayList<>();
// 每落一个正方形,收集一下,所有东西组成的图像,最高高度是什么
for (int[] arr : positions) {
int L = map.get(arr[0]);
int R = map.get(arr[0] + arr[1] - 1);
int height = segmentTree.query(L, R, 1, N, 1) + arr[1];
max = Math.max(max, height);
res.add(max);
segmentTree.update(L, R, height, 1, N, 1);
}
return res;
} 这里的查询和更新操作将求和变为了取最大值,整体的代码框架没有一点变化。
查询操作:
public int query(int L, int R, int l, int r, int rt) {
if (L <= l && r <= R) {
return max[rt];
}
int mid = (l + r) >> 1;
pushDown(rt, mid - l + 1, r - mid);
int left = 0;
int right = 0;
if (L <= mid) {
left = query(L, R, l, mid, rt << 1);
}
if (R > mid) {
right = query(L, R, mid + 1, r, rt << 1 | 1);
}
return Math.max(left, right);
}更新操作:
public void update(int L, int R, int C, int l, int r, int rt) {
if (L <= l && r <= R) {
update[rt] = true;
change[rt] = C;
max[rt] = C;
return;
}
int mid = (l + r) >> 1;
pushDown(rt, mid - l + 1, r - mid);
if (L <= mid) {
update(L, R, C, l, mid, rt << 1);
}
if (R > mid) {
update(L, R, C, mid + 1, r, rt << 1 | 1);
}
pushUp(rt);
}完整代码:
public static class SegmentTree {
private int[] max;
private int[] change;
private boolean[] update;
public SegmentTree(int size) {
int N = size + 1;
max = new int[N << 2];
change = new int[N << 2];
update = new boolean[N << 2];
}
private void pushUp(int rt) {
max[rt] = Math.max(max[rt << 1], max[rt << 1 | 1]);
}
// ln表示左子树元素结点个数,rn表示右子树结点个数
private void pushDown(int rt, int ln, int rn) {
if (update[rt]) {
update[rt << 1] = true;
update[rt << 1 | 1] = true;
change[rt << 1] = change[rt];
change[rt << 1 | 1] = change[rt];
max[rt << 1] = change[rt];
max[rt << 1 | 1] = change[rt];
update[rt] = false;
}
}
public void update(int L, int R, int C, int l, int r, int rt) {
if (L <= l && r <= R) {
update[rt] = true;
change[rt] = C;
max[rt] = C;
return;
}
int mid = (l + r) >> 1;
pushDown(rt, mid - l + 1, r - mid);
if (L <= mid) {
update(L, R, C, l, mid, rt << 1);
}
if (R > mid) {
update(L, R, C, mid + 1, r, rt << 1 | 1);
}
pushUp(rt);
}
public int query(int L, int R, int l, int r, int rt) {
if (L <= l && r <= R) {
return max[rt];
}
int mid = (l + r) >> 1;
pushDown(rt, mid - l + 1, r - mid);
int left = 0;
int right = 0;
if (L <= mid) {
left = query(L, R, l, mid, rt << 1);
}
if (R > mid) {
right = query(L, R, mid + 1, r, rt << 1 | 1);
}
return Math.max(left, right);
}
}
public HashMap index(int[][] positions) {
TreeSet pos = new TreeSet<>();
for (int[] arr : positions) {
pos.add(arr[0]);
pos.add(arr[0] + arr[1] - 1);
}
HashMap map = new HashMap<>();
int count = 0;
for (Integer index : pos) {
map.put(index, ++count);
}
return map;
}
public List fallingSquares(int[][] positions) {
HashMap map = index(positions);
// 100 -> 1 306 -> 2 403 -> 3
// [100,403] 1~3
int N = map.size(); // 1 ~ N
SegmentTree segmentTree = new SegmentTree(N);
int max = 0;
List res = new ArrayList<>();
// 每落一个正方形,收集一下,所有东西组成的图像,最高高度是什么
for (int[] arr : positions) {
int L = map.get(arr[0]);
int R = map.get(arr[0] + arr[1] - 1);
int height = segmentTree.query(L, R, 1, N, 1) + arr[1];
max = Math.max(max, height);
res.add(max);
segmentTree.update(L, R, height, 1, N, 1);
}
return res;
} c++版本:
int max[4100]={};
int update[4100]={};
int change[4100]={};
set allPos;
unordered_map hash;
int cnt = 0;
void init(vector>& positions){
for(vector a:positions){
int L = a[0];
int R = a[0]+a[1]-1;
allPos.insert(L);
allPos.insert(R);
}
// 为每一个位置从左往右编号,防止数字溢出
for(auto it=allPos.begin();it!=allPos.end();++it){
hash[*it] = ++cnt;
}
}
void pushDown(int rt,int lsize,int rsize){
if(update[rt]){
update[rt<<1] = true;
update[rt<<1 | 1] = true;
change[rt<<1] = change[rt];
change[rt<<1 | 1] = change[rt];
max[rt<<1] = change[rt];
max[rt<<1 | 1] = change[rt];
update[rt] = false;
}
}
// 查询[L,R]范围上的高度
// rt为当前根节点下标
// [l,r]为max[rt]所代表的范围
int getHeight(int L,int R,int l,int r,int rt){
if(L<=l&&r<=R){
//[l,r]被[L,R]覆盖
return max[rt];
}
// 无法覆盖,先下发懒更新
int mid = (l+r) >> 1;
pushDown(rt,mid-l+1,r-mid);
// 懒更新任务下发完毕,下发查询任务
int Lheight=0,Rheight=0;
if(L<=mid){
// 左半区间有交集
Lheight = getHeight(L,R,l,mid,rt<<1);
}
if(R>mid){
// 右半区间有交集
Rheight = getHeight(L,R,mid+1,r,rt<<1 | 1);
}
return Lheightmax[rt<<1 | 1]?max[rt<<1]:max[rt<<1 | 1];
}
void updateHeight(int L,int R,int l,int r,int rt,int height){
if(L<=l&&r<=R){
//[l,r]被[L,R]覆盖
max[rt] = height;
update[rt] = true;
change[rt] = height;
return ;
}
// 无法覆盖,先下发懒更新
int mid = (l+r) >> 1;
pushDown(rt,mid-l+1,r-mid);
// 懒更新任务下发完毕,下发更新任务
if(L<=mid){
// 左半区间有交集
updateHeight(L,R,l,mid,rt<<1,height);
}
if(R>mid){
// 右半区间有交集
updateHeight(L,R,mid+1,r,rt<<1 | 1,height);
}
// 汇总
pushUp(rt);
}
vector fallingSquares(vector>& positions) {
init(positions);
int maxHeight = 0;
vector result;
for(vector a:positions){
int L = hash[a[0]];
int R = hash[a[0]+a[1]-1];
// 获得[L,R]返回的最新高度
int height = getHeight(L,R,1,cnt,1) + a[1];
maxHeight = maxHeight