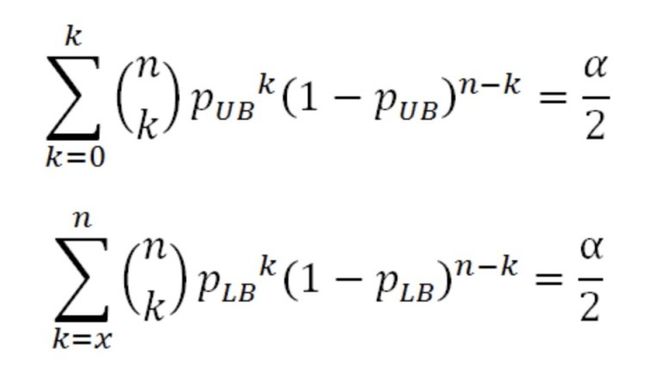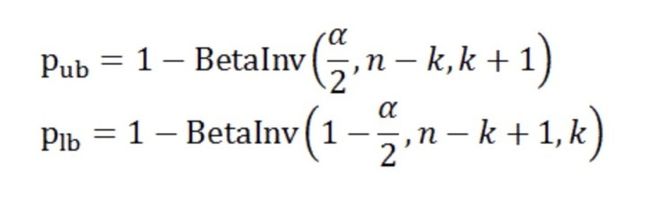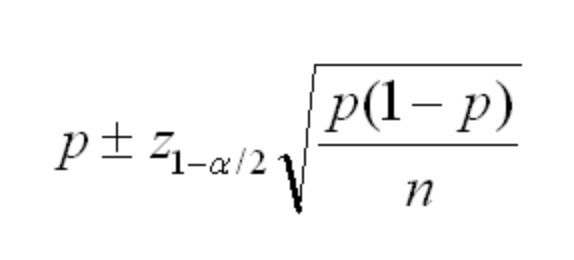前言
日常开发测试可能会遇到这样一种情况,有一个接口或方法概率触发,那么需要多少次抽样,落在一个什么区间内,才能断定是否按照设定概率进行呢?
本文将以二项分布作为研究手段,分两种情况求解此类问题的置信区间范围,并结合实际案例进行分析。
背景
某一天,测试同学在验证一个接口时遇到了一个问题。
该接口设定为50%概率触发,测试同学写了自动化脚本进行多次调用。
但是问题来了,他并不知道应该调用多少次,然后落在一个什么区间内才算测试通过。
极大的扩大样本容量,然后给一个模糊的范围边界确实能解决这个问题,但是测试同学并不满足于此,他要一个精确的数字!
因此我只能满足他任性的要求,提笔拯救测试同学。
解题思路
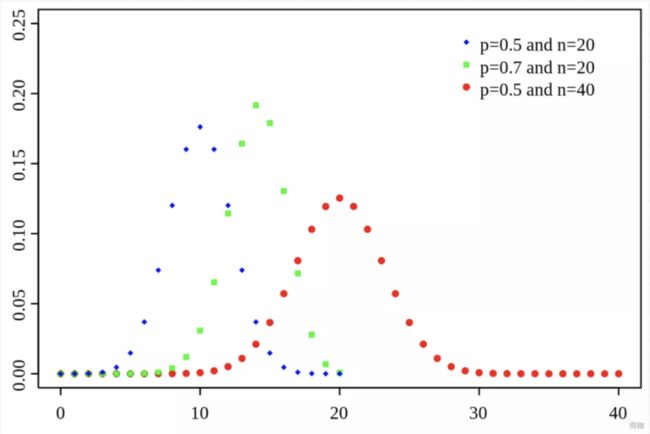
在这种情况下,触发 or 不触发 此类概率问题可以看作一个二项分布,我们的目的在于经过一定量的样本测试之后判断测试出来的概率是否落在置信区间内。
那么就需要考虑这几种极端情况:
1.概率太小
2.概率太大
3.样本数很小
4.样本数很大
在二项分布中,可以将样本数与事件概率综合起来考虑,合并为以下两种情况
(a) 概率比较正常或样本数较大 —— np > 5 and n(1-p) > 5
(b) 概率比较极端或样本数较小 —— np <= 5 or n(1-p) <= 5
(n :样本总数,p:概率)
二项分布的置信区间估计方法常用的有两种,一是正态分布近似方法,即 Normal Approximation Method;二是精确置信区间法,即 Clopper-Pearson Method。
对于这两种情况可分别应用这两种方法进行求解。
Normal Approximation Method
很容易可以想象出当样本数足够大的情况下,二项分布的曲线分布会愈发趋向于近似正态分布。
因此在情况a中适用于正态分布近似。
置信区间计算公式:
因此使用了正态分布近似,因此Z value用的也是正态分布的Z value。
p: 样本中所测得的事件发生概率
a: I类错误率
Z: Z value常量,可查表得知
n: 样本总数
该方法的优点在于简单易于理解,但是在极端情况中精度会很差。
Clopper-Pearson Method
在情况b中适用于精确置信区间法
置信区间计算公式(贼复杂,网上大多数贴的都是这个):
但是可以发现上述公式是基于Binomial Cumulative Distribution Function,可以通过Beta Distribution来计算,因此经过简化可得如下置信区间计算公式。
置信区间计算公式(经过简化):
n: 样本总数
k: 成功数量
a: I类错误率
BetaInv: 一个算法函数,完全不用理解具体细节,找个别人实现的直接调用即可(包括excel)
这样一来就简单的多了,我甚至可以拿excel解出来。
该方法的优点就在于可以处理极端情况,p是0或1的情况也阔以。
实际案例
案例一(正态分布近似法)
问题:一个50%概率的接口,测试50次,成功28次,判断是否正常。
p = 28/50 = 0.56
np = 0.56* 50 = 28 > 5
n(1-p) = 0.45 * 50 = 22 > 5
因此使用正态分布近似法。
置信度假设为95%,因此查表得知Z值为1.96
Z = 1.96
p = 28/50 = 0.56
n = 50
代入可得,置信区间为[0.56 - 0.14, 0.56 + 0.14]这个范围,因此0.5确实落入这个置信区间,所以可以暂时认为这个我这个接口没问题!
案例二(精确置信区间法)
问题:一个17%概率的接口,测试50次,成功3次,判断是否正常。
p = 3 / 50 = 0.06
np = 0.06* 50 = 3 < 5
适用于精确置信区间法。
假设置信度为95%
a = 0.05
n = 50
k = 3
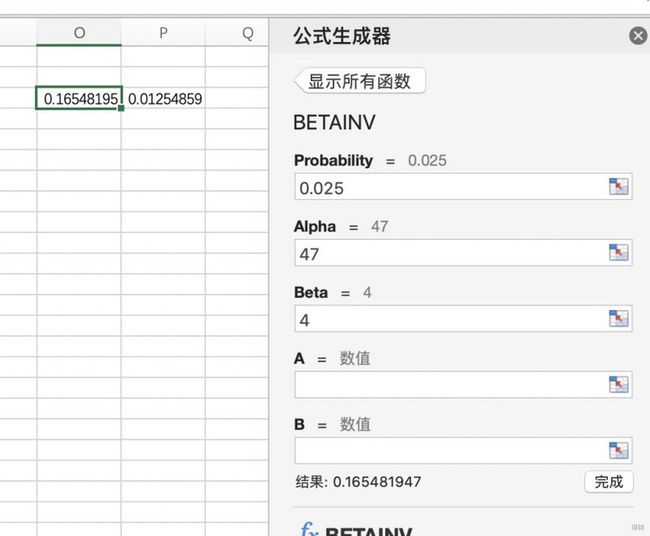
使用Excel或其他方法
计算可得:
Pub = 0.1655
Plb = 0.0125
置信区间为[0.0125, 0.1655],所以17%概率的接口没有落在置信区间内,可以认为在95%置信度的情况下,该接口出现了问题。
接着有请测试同学发言=。=!
测试的实践
实践的功能与背景
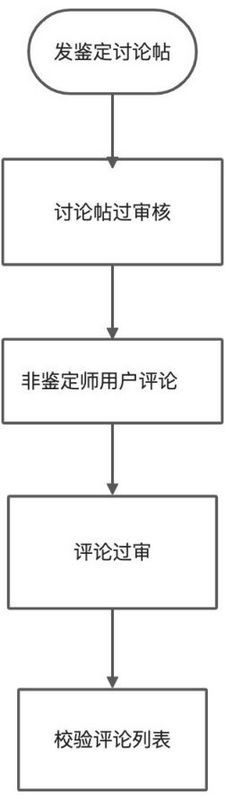
基于鉴定460版ai鉴定师智能回复这个功能。简单来说这个功能就是,当你对鉴定贴进行回复时,你的回复内容完全匹配到回复词库时,就会触发ai自动回复。而触发ai自动回复是有一个概率控制的,在测试的时候想不单单校验返回值,也想同时校验这个概率功能的准确性。
测试执行
首先遇到这个功能,我想到的测试步骤就是:
目前就是这个测试步骤,然后通过接口的返回值来判断做判定:
1.检查回复中有没有子评论
2.检查子评论的回复人是不是ai鉴定师
校验的代码如下
if (replyListResponse.getJSONObject("data").getJSONObject("simpleReply").
getJSONArray("list").getJSONObject(j).getJSONObject("childReply").
getJSONArray("list")!=null){
DuAssert.getInstance().assertTrue(replyListResponse.
getJSONObject("data").getJSONObject("simpleReply").
getJSONArray("list").getJSONObject(j).getJSONObject("childReply").
getJSONArray("list").getJSONObject(0).getString("userName").equals("ai鉴别"));
}有人会问,为什么没有检查回复的信息的正确性呢?首先,测试服的数据不可控因素比较多,比如今天校验了他的回复信息,但是过两天回复信息在验收之后改了,那就还需要对用例进行改动。其次,在正常的测试流程中肯定会覆盖不同的入参信息与不同的返回信息对应情况,只要验证一次这个逻辑,剩下这个数据准确性的验证反而觉得有一些冗余,写针对这么长的测试用例更像是为了保证整个流程:从发帖到审核,从回复到审核这两个老流程的准确性保证;非鉴定师触发ai鉴别这个基础流程的保证情况。
概率验证
进行到概率验证,做法很简单,比如我们随机50次,然后有子评论,且评论用户为ai鉴别,则n+1。但是这样又会引入一个新问题,这个最后叠加出的n肯定是在一定区间内波动的。比如服务端现在设置为50%回复,那n就是25左右,那这个具体要怎样来设置这个区间,才能较为准确的验证这个概率的正确性,从而在数值没有落在区间内的时候,可以光明正大的给开发提bug,说你的概率算的不准确呢?
从上文中我们得知,需要测试的事件概率为50%,尝试的次数为50次,所以:
np=50X50%;
n(1-p)=50X50%,
均大于5,由此可知概率应符合正态分布曲线,所以用来计算这个置信区间的公式为:
代码实现
public static double getProbability(int times,double targetP) {
double z=1.96;
return Math.sqrt(targetP*(1-targetP)/times)*z;
}很简单,一行代码就搞定了。有同学可能会问这个1.96是哪来的,实际上这个是查表查的,暂定要求的准确度为95%,于是根据下方的表格查得0.975对应的横纵坐标为0.06和1.9,于是相加得1.96
最后用例代码添加
double realP=n/50.00;
double max =Math.ceil(50*realP+50* Probability.getProbability(50,realP));
double min =Math.ceil(50*realP-50* Probability.getProbability(50,realP));
if (25<=max &&25>min){
DuAssert.getInstance().assertEquals("在区间内,概率可信","在区间内,概率可信");
}
else{
DuAssert.getInstance().assertEquals("不在区间内,不可信,提bug!","在区间内,概率可信");
}综上所述,我们基于统计的原理校验了这个功能的准确性。
总结
测试概率是测试过程中一个比较模棱两可的事情,如何进行概率事件的测试并有效的发现问题是非常必要的。
因此在上文中主要将此类问题模拟成二项分布进行求解,求得置信区间从而进行较为准确的判断。
但是有一点要注意的是在上文两个案例中都是以95%置信度作为前提,实际上是存在发生I类错误的可能性,所以测出了问题只能说大概率可能出现了问题,而不能立马给一个绝对性的结论,这样是不科学的。
建议是根据统计学经验,先测30+次,能用正态分布近似覆盖就尽量先使用正态分布近似。