复旦大学961-数据结构-第三章-查找(4)平衡树(AVL)的定义,性质,ADT及其实现,平衡树查找,插入算法,平衡因子的概念
961全部内容链接
文章目录
- 平衡二叉树(AVL)的定义
- 平衡二叉树的性质
- 平衡二叉树的ADT
-
- 平衡树的查找
- 平衡树的插入
-
-
- LL(右单旋转)
- RR(左单旋转)
- RL(先右后左旋转)
- LR(先左后右旋转)
-
- 平衡树的插入Java实现
- 平衡树的删除
- 完整代码如下
平衡二叉树(AVL)的定义
在上一节中,提到了BST(二叉排序树),它的最坏查找时间复杂度为O(n)。若插入顺序是有序的,就会产生这种现象。为了解决这个问题,所以引出了平衡树。平衡树也是一棵BST,只不过它有更多的约束条件。即每个节点的左右子树的高度不能差太多。
即一棵二叉排序树,若该树的所有节点的左子树和右子树的高度之差不超过1,则该树称为平衡二叉树,简称平衡树,又称AVL树(AVL是发明人名字的字母缩写),也称BT(Balanced Binary Tree)。
其中左右子树的高度之差称为平衡因子。 在平衡二叉树中,平衡因子只可能是-1,0,1。
平衡二叉树的性质
除了定义中提到的性质,还具有二叉排序树的一切性质。除此之外,
- 含有n个节点的平衡二叉树的最大深度为 O ( log 2 n ) O(\log_2n) O(log2n)
- 由(1)知,平衡二叉树的查找时间复杂度为 O ( log 2 n ) O(\log_2n) O(log2n)
平衡二叉树的ADT
public class AvlTree<AnyType extends Comparable<? super AnyType>> {
private static class AvlNode<AnyType> {
AnyType element;
AvlNode<AnyType> left;
AvlNode<AnyType> right;
int height;
public AvlNode(AnyType theElement) {
this.element = theElement;
}
}
private AvlNode<AnyType> root;
public AvlTree() {
root = null;
}
public boolean contains(AnyType x) {
}
public void insert(AnyType x) {
}
public void remove(AnyType x) {
}
}
平衡树的查找
与二叉排序树的查找没有区别
平衡树的插入
平衡树的插入要比二叉排序树的插入算法要复杂一些,前面的和二叉排序树一样,但是插入的最后,要对其进行“调整”操作,目的是保证该二叉排序树是一棵平衡树。
先理解一个概念,最小不平衡子树,就是指在一棵树中,最小的那个不平衡的子树,就是最小不平衡子树。如图所示:

在该树中,以50为根节点的子树和以66为根节点的子树,它们俩的平衡因子都是-2,以70为根节点的子树,它的最小不平衡因子为2,但是70那棵子树是这三棵子树中最小的那棵,所以70是最小不平衡子树。 对二叉树的调整都是调整最小不平衡子树。
主要分为以下情况:
LL(右单旋转)
LL:左孩子的左孩子导致树不平衡。此时应该使用右旋转,即将根节点(最小子树的根节点)的左孩子作为根节点,然后根节点变成它左孩子的右孩子。如图:
在该图中,最小不平衡子树为678这棵。以根节点的左孩子为轴心,向右旋转,即将7节点作为新的根节点,8节点作为7节点的右孩子
RR(左单旋转)
RR:与LL正好相反。由右孩子的右孩子导致的不平衡,则使用左单旋转,即将根节点的右孩子作为新的根节点,原来的根节点作为新根节点的左孩子。如图:
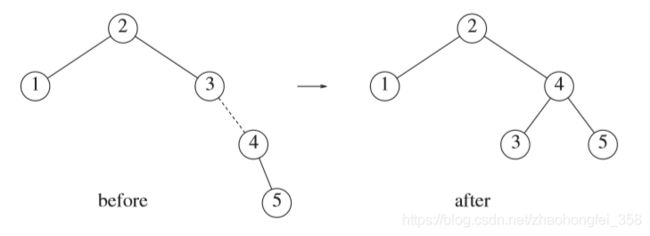
在该图中,345为最小不平衡子树。进行左单旋转,以4为轴线,向左旋转。即4作为新的根节点,3作为4的左孩子。
特殊的,如果根节点的右孩子有左孩子,则该左孩子需要链接到原根节点的右孩子,如图所示:

该树为一棵树中的最小不平衡子树,该树进行旋转,依照上面的原则,以4为轴心,将4作为新的根节点,2作为4的左孩子,但是因为4已经有左孩子了,所以需要将4的左孩子链接到2的右孩子上。
RL(先右后左旋转)
RL:由右孩子的左孩子引起的不平衡。需要先进行右旋转,再进行左旋转。 右旋转指的是不平衡子树的右子树进行右旋转,即右单旋转。然后不平衡子树就会变成RR型,然后再对整个不平衡子树进行左单旋转即可。如图所示:

在该图中,最小不平衡子树为 7 16 15,属于RL型,所以第一步是对 16 15 这个节点进行右单旋转,变成 15 16(图中没有体现)。这样整个不平衡子树就变成了 7 15 16,即RR型。然后再对整个不平衡子树进行左单旋转,就变成了图二所示的样子。
例二:
在该图中,最小不平衡子树为6为根节点的子树。也是RL型,所以先对15这个子树进行右单6旋转,然后变成右图中k2,k3那部分(图中没有具体体现中间过程)。然后再对6这整个子树进行左单旋转,就变成了右图中的结果。
LR(先左后右旋转)
LR:与RL相反,不平衡子树是由左子树的右子树引起的。所以先对不平衡子树的左子树进行左单旋转,然后再对整个不平衡子树进行右单旋转。TODO,暂时没找到合适的图,没有具体例子,建议先把上面3个看懂。等考完试我再慢慢补充吧。
平衡树的插入Java实现
private int height(AvlNode x) {
// 返回节点的高度,若节点为空,则认为高度为-1,若不为空,则返回节点高度
return x == null ? -1 : x.height;
}
public void insert(AnyType x) {
root = insert(root, x);
// printTree(); // 打印过程,查看变换过程
// System.out.println("------------------------------------");
}
private AvlNode insert(AvlNode<AnyType> node, AnyType x) {
if (node == null) return new AvlNode<>(x);
int result = x.compareTo(node.element);
if (result > 0) {
// x需要插入到右子树中
node.right = insert(node.right, x);
} else if (result < 0) {
// x需要插入到左子树中
node.left = insert(node.left, x);
} else {
// nothing to do
}
// 前面的代码和二叉搜索树没有区别
return balance(node); // 插入完成后,对其进行调整操作。使树保持平衡。
// 该递归可以使得每次插入位置依次往上调整,每层都进行判断“是否存在不平衡子树”
}
private AvlNode balance(AvlNode node) {
if (node == null) return null; // 这个如果remove节点时,会出现null的情况,所以需要加判断
int factor = height(node.left) - height(node.right); // 计算该节点的平衡因子
if (factor > 1) {
// 左子树比右子树高,需要调节左子树
node = balanceLeft(node);
} else if (factor < -1) {
// 右子树比左子树高,需要调节左子树
node = balanceRight(node);
} else {
// factor == -1,0,1,不存在不平衡,不需要调整
}
// 更新该节点的高度。该高度是以该节点作为根节点时,子树的高度。当为空节点时为-1,当为单个节点时为0,与书上有些区别。
node.height = Math.max(height(node.left), height(node.right)) + 1;
return node;
}
private AvlNode balanceLeft(AvlNode node) {
int factor = height(node.left.left) - height(node.left.right); // 计算该节点左孩子的平衡因子
if (factor >= 0) {
// 左子树比右子树高(或相等),再加上这是调节左子树,说明是个LL型,需要进行右单旋转
node = rightRotate(node);
} else if (factor < 0) {
// 右子树比左子树高,说明是LR型,需要左旋转,再右旋转
node.left = leftRotate(node.left); // 对左子树进行左旋转
node = rightRotate(node); // 对整个不平衡子树进行右旋转
}
return node;
}
private AvlNode balanceRight(AvlNode node) {
int factor = height(node.right.left) - height(node.right.right); // 计算该节点右孩子的平衡因子
if (factor > 0) {
// 左子树比右子树高,再加上这是调节右子树,说明是个RL型,需要先右旋转,再左旋转
node.right = rightRotate(node.right); // 对右子树进行右旋转
node = leftRotate(node); //对整体进行左旋转
} else if (factor <= 0) {
// 右子树比左子树高(或相等),说明是RR型,需要左单旋转
node = leftRotate(node); // 对整个不平衡子树进行左单旋转
}
return node;
}
// 左单旋转
private AvlNode leftRotate(AvlNode node) {
AvlNode root = node.right; // node的右孩子作为新的根节点
node.right = root.left; // 新的根节点的左孩子链接到原节点的右孩子上
root.left = node; // 原节点作为新的根节点的左孩子
// 重新计算高度
root.left.height = Math.max(height(root.left.left), height(root.left.right)) + 1; // 新根节点的左子树高度改变了
root.height = Math.max(height(root.left), height(root.right)) + 1; // 新根节点的右子树高度改变了
return root; // 返回新的根节点
}
// 右单旋转
private AvlNode rightRotate(AvlNode node) {
AvlNode root = node.left; // node的左孩子作为新的根节点
node.left = root.right; // 新的根节点的右孩子作为原节点的左孩子
root.right = node; // 原节点作为新根节点的右孩子。
// 重新计算高度
root.right.height = Math.max(height(root.right.left), height(root.right.right)) + 1; // 新根节点的右子树高度改变了
root.height = Math.max(height(root.left), height(root.right)) + 1; // 新根节点的高度也改变了
return root; //返回新的根节点
}
该代码与书上的代码不一致,没有进行中间步骤的省略。个人认为虽然冗余,但是思路比较清晰。
其中涉及到几个比较关键的知识点,我认为考试的时候有可能单独考察,毕竟考察整个代码不太可能,太多了:
- LL型,RR型,LR型和RL型如何旋转
- 左单旋转和右单旋转的具体代码实现
- 旋转过程中,高度的重新计算
以上三个,有时间展开讲解,TODO
平衡树的删除
平衡树的删除操作与二叉排序树的删除操作基本一致,区别在于最后要对节点进行“调整(balance)”操作。代码如下:
public void remove(AnyType x) {
root = remove(root, x);
root = balance(root);
}
private AvlNode remove(AvlNode<AnyType> node, AnyType x) {
if (node == null) return null; // 查找失败
int result = x.compareTo(node.element);
if (result > 0) {
// 要删除的x在右子树上
node.right = remove(node.right, x);
} else if (result < 0) {
// 要删除的x在左子树上
node.left = remove(node.left, x);
} else {
// 找到了要删除的节点
if (node.left != null && node.right != null) {
// 左孩子和右孩子都不为空,则从右子树中找到最小值,然后替换该节点,再删除右子树中的最大节点
AvlNode minNode = findMin(node.right);
node.element = (AnyType) minNode.element;
node.right = remove(node.right, node.element);
} else {
node = (node.left != null) ? node.left : node.right;
}
}
return balance(node);
}
完整代码如下
public class AvlTree<AnyType extends Comparable<? super AnyType>> {
private static class AvlNode<AnyType> {
AnyType element;
AvlNode<AnyType> left;
AvlNode<AnyType> right;
int height;
public AvlNode(AnyType theElement) {
this.element = theElement;
}
}
private AvlNode<AnyType> root;
public AvlTree() {
root = null;
}
private boolean contains(AvlNode<AnyType> node, AnyType x) {
if (node == null) return false; // 如果都空了还没找到,那么就是不存在
int result = x.compareTo(node.element);
if (result == 0) return true; // 查找成功
else if (result > 0) return contains(node.right, x); // x在右子树中
else return contains(node.left, x); // x在左子树中
}
public boolean contains(AnyType x) {
return contains(root, x);
}
private int height(AvlNode x) {
// 返回节点的高度,若节点为空,则认为高度为-1,若不为空,则返回节点高度
return x == null ? -1 : x.height;
}
public void insert(AnyType x) {
root = insert(root, x);
// printTree(); // 打印过程,查看变换过程
// System.out.println("------------------------------------");
}
private AvlNode insert(AvlNode<AnyType> node, AnyType x) {
if (node == null) return new AvlNode<>(x);
int result = x.compareTo(node.element);
if (result > 0) {
// x需要插入到右子树中
node.right = insert(node.right, x);
} else if (result < 0) {
// x需要插入到左子树中
node.left = insert(node.left, x);
} else {
// nothing to do
}
// 前面的代码和二叉搜索树没有区别
return balance(node); // 插入完成后,对其进行调整操作。使树保持平衡。
// 该递归可以使得每次插入位置依次往上调整,每层都进行判断,是否存在不平衡子树
}
private AvlNode balance(AvlNode node) {
if (node == null) return null; // 这个如果remove节点时,会出现null的情况,所以需要加判断
int factor = height(node.left) - height(node.right); // 计算该节点的平衡因子
if (factor > 1) {
// 左子树比右子树高,需要调节左子树
node = balanceLeft(node);
} else if (factor < -1) {
// 右子树比左子树高,需要调节左子树
node = balanceRight(node);
} else {
// factor == -1,0,1,不存在不平衡,不需要调整
}
// 更新该节点的高度。该高度是以该节点作为根节点时,子树的高度。当为空节点时为-1,当为单个节点时为0,与书上有些区别。
node.height = Math.max(height(node.left), height(node.right)) + 1;
return node;
}
private AvlNode balanceLeft(AvlNode node) {
int factor = height(node.left.left) - height(node.left.right); // 计算该节点左孩子的平衡因子
if (factor >= 0) {
// 左子树比右子树高(或相等),再加上这是调节左子树,说明是个LL型,需要进行右单旋转
node = rightRotate(node);
} else if (factor < 0) {
// 右子树比左子树高,说明是LR型,需要左旋转,再右旋转
node.left = leftRotate(node.left); // 对左子树进行左旋转
node = rightRotate(node); // 对整个不平衡子树进行右旋转
}
return node;
}
private AvlNode balanceRight(AvlNode node) {
int factor = height(node.right.left) - height(node.right.right); // 计算该节点右孩子的平衡因子
if (factor > 0) {
// 左子树比右子树高,再加上这是调节右子树,说明是个RL型,需要先右旋转,再左旋转
node.right = rightRotate(node.right); // 对右子树进行右旋转
node = leftRotate(node); //对整体进行左旋转
} else if (factor <= 0) {
// 右子树比左子树高(或相等),说明是RR型,需要左单旋转
node = leftRotate(node); // 对整个不平衡子树进行左单旋转
}
return node;
}
// 左单旋转
private AvlNode leftRotate(AvlNode node) {
AvlNode root = node.right; // node的右孩子作为新的根节点
node.right = root.left; // 新的根节点的左孩子链接到原节点的右孩子上
root.left = node; // 原节点作为新的根节点的左孩子
// 重新计算高度
root.left.height = Math.max(height(root.left.left), height(root.left.right)) + 1; // 新根节点的左子树高度改变了
root.height = Math.max(height(root.left), height(root.right)) + 1; // 新根节点的右子树高度改变了
return root; // 返回新的根节点
}
// 右单旋转
private AvlNode rightRotate(AvlNode node) {
AvlNode root = node.left; // node的左孩子作为新的根节点
node.left = root.right; // 新的根节点的右孩子作为原节点的左孩子
root.right = node; // 原节点作为新根节点的右孩子。
// 重新计算高度
root.right.height = Math.max(height(root.right.left), height(root.right.right)) + 1; // 新根节点的右子树高度改变了
root.height = Math.max(height(root.left), height(root.right)) + 1; // 新根节点的高度也改变了
return root; //返回新的根节点
}
public void remove(AnyType x) {
root = remove(root, x);
root = balance(root);
System.out.println("------------------------------------------");
printTree();
}
private AvlNode remove(AvlNode<AnyType> node, AnyType x) {
if (node == null) return null; // 查找失败
int result = x.compareTo(node.element);
if (result > 0) {
// 要删除的x在右子树上
node.right = remove(node.right, x);
} else if (result < 0) {
// 要删除的x在左子树上
node.left = remove(node.left, x);
} else {
// 找到了要删除的节点
if (node.left != null && node.right != null) {
// 左孩子和右孩子都不为空,则从右子树中找到最小值,然后替换该节点,再删除右子树中的最大节点
AvlNode minNode = findMin(node.right);
node.element = (AnyType) minNode.element;
node.right = remove(node.right, node.element);
} else {
node = (node.left != null) ? node.left : node.right;
}
}
return balance(node);
}
private AvlNode<AnyType> findMin(AvlNode<AnyType> node) {
if (node.left == null) return node;
return findMin(node.left); // 递归查找左孩子
}
// 用于获得树的层数
public static int getTreeDepth(AvlNode node) {
return node == null ? 0 : (1 + Math.max(getTreeDepth(node.left), getTreeDepth(node.right)));
}
private static void writeArray(AvlNode currNode, int rowIndex, int columnIndex, String[][] res, int treeDepth) {
// 保证输入的树不为空
if (currNode == null) return;
// 先将当前节点保存到二维数组中
res[rowIndex][columnIndex] = String.valueOf(currNode.element);
// 计算当前位于树的第几层
int currLevel = ((rowIndex + 1) / 2);
// 若到了最后一层,则返回
if (currLevel == treeDepth) return;
// 计算当前行到下一行,每个元素之间的间隔(下一行的列索引与当前元素的列索引之间的间隔)
int gap = treeDepth - currLevel - 1;
// 对左儿子进行判断,若有左儿子,则记录相应的"/"与左儿子的值
if (currNode.left != null) {
res[rowIndex + 1][columnIndex - gap] = "/";
writeArray(currNode.left, rowIndex + 2, columnIndex - gap * 2, res, treeDepth);
}
// 对右儿子进行判断,若有右儿子,则记录相应的"\"与右儿子的值
if (currNode.right != null) {
res[rowIndex + 1][columnIndex + gap] = "\\";
writeArray(currNode.right, rowIndex + 2, columnIndex + gap * 2, res, treeDepth);
}
}
public void printTree() {
AvlNode node = root;
if (node == null) System.out.println("EMPTY!");
// 得到树的深度
int treeDepth = getTreeDepth(node);
// 最后一行的宽度为2的(n - 1)次方乘3,再加1
// 作为整个二维数组的宽度
int arrayHeight = treeDepth * 2 - 1;
int arrayWidth = (2 << (treeDepth - 2)) * 3 + 1;
// 用一个字符串数组来存储每个位置应显示的元素
String[][] res = new String[arrayHeight][arrayWidth];
// 对数组进行初始化,默认为一个空格
for (int i = 0; i < arrayHeight; i++) {
for (int j = 0; j < arrayWidth; j++) {
res[i][j] = " ";
}
}
// 从根节点开始,递归处理整个树
// res[0][(arrayWidth + 1)/ 2] = (char)(node.val + '0');
writeArray(node, 0, arrayWidth / 2, res, treeDepth);
// 此时,已经将所有需要显示的元素储存到了二维数组中,将其拼接并打印即可
for (String[] line : res) {
StringBuilder sb = new StringBuilder();
for (int i = 0; i < line.length; i++) {
sb.append(line[i]);
if (line[i].length() > 1 && i <= line.length - 1) {
i += line[i].length() > 4 ? 2 : line[i].length() - 1;
}
}
System.out.println(sb.toString());
}
}
public static void main(String[] args) {
AvlTree<Integer> tree = new AvlTree<>();
tree.insert(10);
tree.insert(20);
tree.insert(30);
tree.insert(50);
tree.insert(40);
tree.insert(25);
tree.insert(60);
tree.insert(70);
tree.insert(80);
tree.insert(90);
tree.insert(100);
tree.printTree();
tree.remove(70);
tree.remove(50);
tree.remove(60);
tree.remove(40);
tree.remove(90);
tree.remove(100);
tree.remove(80);
}
}