复旦大学961-数据结构-第五章-图（三）最小生成树基本概念,Prim算法,Kruskal算法

961全部内容链接

最小生成树的概念

首先，最小生成树是针对①连通图和②带权图的。生成树就是对一个连通图砍掉一些边，然后将这个图变成一个树。而最小生成树（Minimum-Spanning-Tree，MST）就是，如何砍边，然后能让这棵树的权值最小。

最小生成树具有以下特点：

1. 最小生成树不唯一。一个图可以可能对应多个最小生成树
2. 最小生成树的权值唯一。虽然树不唯一，但是他们的权值一定是唯一的，且是最小的。
3. 最小生成树的边数等于顶点数减1。这是树的性质

带权图ADT及其实现

public interface WeightedGraph<VertexType> extends Graph<VertexType> {
     

    int getEdgeWeight(VertexType x, VertexType y); // 获取(x,y)边的权值

    void addEdge(VertexType x, VertexType y, int weight); // 插入边  或 (x,y)

}

带权图的ADT继承自普通图，多了获取边的权值。增添边时需要多传一个权值的参数。

具体实现如下：

// 邻接矩阵无向带权图
public class AdjacencyMatrixUndirectedWeightedGraph<VertexType>
        extends AdjacencyMatrixUndirectedGraph<VertexType>
        implements WeightedGraph<VertexType> {
     

    public AdjacencyMatrixUndirectedWeightedGraph(int maxVertexNum) {
     
        super(maxVertexNum);
    }

    @Override
    public int getEdgeWeight(VertexType x, VertexType y) {
     
        return edges[findIndex(x)][findIndex(y)];
    }

    @Override
    public void addEdge(VertexType x, VertexType y, int weight) {
     
        int xIndex = findIndex(x);
        int yIndex = findIndex(y);
        edges[xIndex][yIndex] = weight;  // 因为是无向图，所以 (x,y)和(y,x)都要为weight
        edges[yIndex][xIndex] = weight;
    }
}

这是邻接矩阵方式实现的无向带权图。也是继承了之前的无权图。具体的无权图代码可以看之前的章节。

Prim算法

prim算法是用于构造最小生成树的，大致思想如下：

1. 首先树中选取一个顶点，一般取第一个。将其加到树T（最开始为空树）中
2. 然后距离树T最近的一个顶点。最开始只有一个顶点，所以就是选取距离该顶点最近的顶点。
3. 将距离树最近的节点加入树中
4. 循环2,3步骤，直到所有的顶点都加入到树中。

如图：

public static WeightedGraph prim(WeightedGraph graph) {
     
    // 使用带权图的形式存储树
    WeightedGraph resultGraph = new AdjacencyMatrixUndirectedWeightedGraph(graph.getVertexNumber());

    Object initVertex = graph.getVertexByIndex(0);  // 选择第一个顶点作为起始顶点
    resultGraph.insertVertex(initVertex);  // 将起始节点插入树
    while (resultGraph.getVertexNumber() < graph.getVertexNumber()) {
      // 若树中的节点小于图中的节点，则说明还有节点没有加入树中
        Object[] treeVertexes = resultGraph.getVertexes(); // 获取当前树中的所有节点
        Object[] closetVertex = findClosestVertex(treeVertexes, graph); // 找出图中距离该树最近的一个节点，并返回树的节点和图的节点
        Object x = closetVertex[0]; // x为树的节点，y为图中的节点。意思是：图中的y节点距离树中的x节点最近
        Object y = closetVertex[1];
        resultGraph.insertVertex(y);  // 将y节点插入树
        resultGraph.addEdge(x, y, graph.getEdgeWeight(x, y)); // 增加(x,y)这条边，权值就是图中(x,y)边的权值
    }
    return resultGraph;
}

// 找出图中距离这棵树最近的节点，并返回树的节点和图的节点
private static Object[] findClosestVertex(Object[] treeVertexes, WeightedGraph graph) {
     
    HashSet treeVertexesSet = new HashSet(Arrays.asList(treeVertexes)); // 将树节点变成HashSet用于比较是否该节点在树中
    int minWeight = Integer.MAX_VALUE;  // 初始化最小权值为无穷
    Object treeVertex = null;  // 图中的closestVertex节点距离树中的treeVertex节点最近
    Object closestVertex = null;
    for (int i = 0; i < treeVertexes.length; i++) {
       // 遍历树的所有节点，找出距离该树最近的节点
        Object[] neighbors = graph.neighbors(treeVertexes[i]);  // 获取树节点i的所有邻接节点

        for (int j = 0; j < neighbors.length; j++) {
        // 遍历所有i的邻接节点，找出最小的那个
            if (!treeVertexesSet.contains(neighbors[j]) &&  // 若该邻接节点不是树中的节点，且距离不为0（定义0为不可达），并且该权值小于最小权值
                    graph.getEdgeWeight(treeVertexes[i], neighbors[j]) > 0 &&
                    graph.getEdgeWeight(treeVertexes[i], neighbors[j]) < minWeight) {
     
                minWeight = graph.getEdgeWeight(treeVertexes[i], neighbors[j]);  // 满足if条件，则更改最小权值
                treeVertex = treeVertexes[i]; // 记录当前权值最小的两个节点。
                closestVertex = neighbors[j];
            }
        }
    }
    return new Object[]{
     treeVertex, closestVertex};
}

复杂度分析（王道解释）：
Prim算法的时间复杂度为O(|V|^2)，不依赖于|E|，因此它适合求解边稠密的图的最小生成树。虽然采用其他方法能改进Prim算法的时间复杂度，但增加了实现的复杂性。

Kruskal算法

这个算法也是求最小生成树的，不过它是依赖边的。大致思想如下：

1. 先初始化树所有的节点。没有任何边。
2. 然后从图中选取一条权值最小的边，连接树中相应的节点。
3. 重复2操作，若边使得树形成了回路，则舍弃该条边。然后继续2
4. 直到边的数量=节点数量-1时，即连通分量数为1，查找完成。

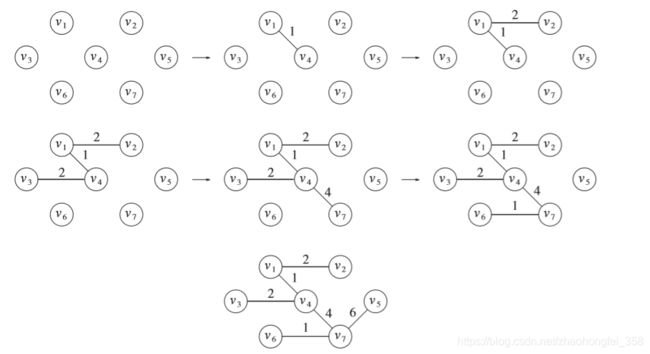
举例，这是Kruskal算法的过程。

算法需要解决的两个关键问题：

• 如何找出当前最小的边？这个简单，只需对当前所有边进行排序，然后从小到大依次取就行了。更好的方式是使用最小堆来每次选择一个最小的元素。
• 如何判断加入当前边后，树是否形成了回路？如上图，最开始为7个节点，可以将这七个节点看成是7个连通分量，加入一条表。连通分量就会减1，当连通分量数量为1时，则构建完成。在这个过程中，若加入的边的两个节点属于同一个连通分量，则一定会形成回路。若两个节点属于不同的连通分量，则一定不会形成回路。

Java代码如下：

    public static WeightedGraph kruskal(WeightedGraph graph) {
     
        WeightedGraph treeGraph = new AdjacencyMatrixUndirectedWeightedGraph(graph.getVertexNumber());  // 使用带全图的方式存储最小生成树
        for (int i = 0; i < graph.getVertexNumber(); i++) {
       // 初始化树中的节点
            treeGraph.insertVertex(graph.getVertexByIndex(i));
        }

        Union union = new Union(Arrays.asList(treeGraph.getVertexes()));  // 将所有节点加入并查集
        int n = treeGraph.getVertexNumber();  // 记录当前连通分量的数量
        BinaryHeap heapEdge = new BinaryHeap(graph.getEdges());  // 使用图的边构建一个最小堆

        while (n > 1) {
       // 如果连通分量的数量为1时，说明最小生成树已经生成。
            WeightedGraph.Edge edge = (WeightedGraph.Edge) heapEdge.deleteMin();  // 从最小堆中拿出最小的那条边 
            if (union.isConnected(edge.vertex1, edge.vertex2)) continue;  // 判断这条边的两个节点是否属于同一个连通分量，即加入该条边后是否会形成回路，如果会，则舍弃这条边
            union.union(edge.vertex1, edge.vertex2);  // 将这条边的两个节点合并成到一个连通分量中
            treeGraph.addEdge(edge.vertex1, edge.vertex2, edge.weight);  // 将树中的这两个节点连接起来
            n--;  // 连通分量的数量-1
        }

        return treeGraph;
    }

这个算法不长，但是用到了之前章节学到的两个重要的数据结构。一个是并查集（961大纲中没有）。另一个是堆。其中堆的代码在之前就有。

这里给出并查集的Java实现：

// 并查集
public class Union<AnyType> {
     

    private Map<AnyType/*当前节点*/, AnyType/*当前节点的父节点*/> map; // 存储并查集

    public Union(Collection<AnyType> collection) {
     
        map = new HashMap<>();
        // 初始化并查集
        for (AnyType item: collection) {
     
            map.put(item, item); // 初始条件下，定义各个元素的父节点就是它自身，即该集合的根节点就是它自己
        }
    }

    // 将并查集中的两个不相连的元素x,y合并成一个
    public void union(AnyType x, AnyType y) {
     
        AnyType xRoot = findRoot(x); // 找出x所在集合的根节点
        AnyType yRoot = findRoot(y); // 找出y所在集合的根节点
        map.put(yRoot, xRoot);  // 将y所在集合的根节点连接到x的根节点上
    }

    // 判断x,y两个节点是否连接
    public boolean isConnected(AnyType x, AnyType y) {
     
        return findRoot(x) == findRoot(y);  // 如果x,y同属于一个根节点，则说明他们两个互相连接
    }

    // 找出x节点的根节点
    private AnyType findRoot(AnyType x) {
     
        // 如果自身等于自身，说明找到根节点，否则就将x赋值为它的父节点。
        while (!map.get(x).equals(x)) {
     
            x = map.get(x);
        }
        return x;
    }
}

因为kruskal算法需要获取到图的所有边，所以WeightEdge中增加了一个抽象方法：

public interface WeightedGraph<VertexType> extends Graph<VertexType> {
     

    static class Edge implements Comparable<Edge> {
     

        public int weight; // 边的权值
        public Object vertex1;  // 变得
        public Object vertex2;  // 该边连接的两个节点

        public Edge(int theWeight, Object theVertex1, Object theVertex2) {
     
            this.weight = theWeight;
            this.vertex1 = theVertex1;
            this.vertex2 = theVertex2;
        }

        @Override
        public int compareTo(Edge o) {
     
            return Integer.compare(weight, o.weight);
        }
    }

    List<Edge> getEdges(); // 返回所有的边
    
    int getEdgeWeight(VertexType x, VertexType y); // 获取(x,y)边的权值

    void addEdge(VertexType x, VertexType y, int weight); // 插入边  或 (x,y)
}

邻接矩阵的具体实现为：

public List<Edge> getEdges() {
     
    ArrayList<Edge> edgeList = new ArrayList<>();
    for (int i = 0; i < edges.length; i++) {
     
        for (int j = i+1; j < edges[i].length; j++) {
     
            if (edges[i][j] != 0) {
     
                edgeList.add(new Edge(edges[i][j], vertexes[i], vertexes[j]));
            }
        }
    }
    return edgeList;
}

复杂度分析（王道）：
通常在Kruskal算法中，使用堆来存放边的集合，因此每次选择最小权值的边只需要O(log|E|)的时间。由于总共有|E|条边，所以总时间复杂度为O(|E|log|E|)。所以这个适合稀疏图