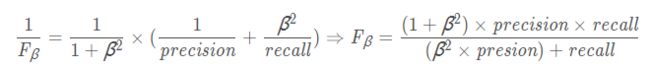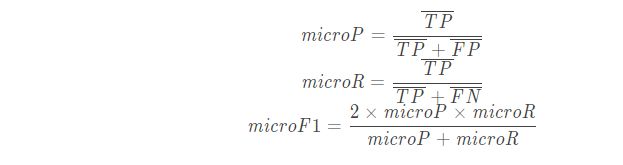机器学习笔记三——模型评估与选择2——性能度量(分类问题）

对学习器的泛化性能进行评估，不仅需要有效可行的实验估计方法，还需要有衡量模型泛化能力的评价标准，这就是性能度量 （performance measure）。

性能度量反映了任务需求，在对比不同模型的能力时，使用不同的性能度量往往会导致不同的评判结果。这意味着模型的‘好坏’是相对的，什么样的模型是好的，不仅取决于算法和数据，还决定于任务需求。

在预测任务中，给定数据集 D=$(x_1,y_1),(x_2,y_2),...,(x_m,y_m)$，其中$y_i$ 是示例$x_i$ 的真实标记。要估计学习器 f 的性能，就要把学习器预测结果 f(x)与真实标记 y 进行比较。

为了说明各性能度量指标，我们以鸢尾花数据集为例，模型选择决策树 CART 算法，通过 train_test_split() 划分数据集，最后评估各项性能指标。

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split


# 引入数据集
dataset = load_iris()
data = dataset.data
target = dataset.target
features = dataset.feature_names

# 划分数据集以及模型训练
data_train, data_test, target_train, target_test = train_test_split(data, target, test_size=0.33, random_state=7)
model = DecisionTreeClassifier()
model.fit(data_train, target_train)

1、错误率和精度

错误率： 在分类任务中，错分的样本数占样本总数的比例称为错误率（error rate）。

精度 = 1 - 错误率。

错误率和精度，是分类任务中最常用的两种性能度量，即适用于二分类任务，也适用于多分类任务。

【代码实现】

from sklearn.metrics import accuracy_score
accuracy_score(target_test,model.predict(data_test))
#输出：0.94

【精度的局限性】
当负样本占 99% 时，分类器把所有样本都预测为负样本也可以获得 99% 的准确率。所以，当不同类别的样本比例非常不均衡时，占比大的类别往往成为影响精度的最主要因素。虽然模型的整体分类精度高，但不代表对占比小的类别的分类精度也高。

解决方案： 平均精度——每个类别下的样本精度的算术平均。例如一个二分类问题，分类 0 共有 270 个样本，其中正确的有 240；分类 1 共有 30 个样本，其中正确的有 24。最终计算出的精度为 (240 + 24) / 300 = 0.88，而平均精度为 (240 / 270 + 24 / 30) / 2 = 0.844。可以看出在分类不均衡情况下，平均精度比精度更能反映客观情况。

【代码实现】

from sklearn.metrics import balanced_accuracy_score

balanced_accuracy_score(target_test, model.predict(data_test))
# 输出：0.944

2、查准率，查全率，混淆矩阵，P-R 曲线，F1

假设我们正常处理一个二分类问题，按照模型预测值和真实值可以把测试样本划分为四种情形：真正例（true positive），假正例（false positive），真反例（true negative），假反例（false negative）。可以把结果表示为下图这个矩阵——混淆矩阵(confusion matrix)。

真实情况	预测结果	预测结果
	正例	反例
正例	TP（真正例）	FN（假反例)
反例	FP（假正例）	TN（真反例）

显然有TP+FP+TN+FN=样例总数。

查准率：又称准确率（precision），在所有被预测为正类的样本中真实结果也为正类的占比。也就是说，分类正确的正样本个数占分类器判定为正样本的样本个数的比例。其用于衡量模型避免错误的能力。
$$P=\frac{TP}{TP+FP}$$

查全率：又称召回率（recall）， 在所有真实结果为正类的样本中预测结果也为正类的占比。也就是说，分类正确的正样本个数占真正的正样本个数的比例。其用于衡量模型避免缺漏的能力。

$$R=\frac{TP}{TP+FN}$$

【查准率和查全率代码实现】

from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
print(precision_score(target_test, model.predict(data_test), average='weighted'))
# 输出：0.941
print(recall_score(target_test, model.predict(data_test), average='weighted'))
# 输出：0.94

\quad \quad 需要注意的是，precision_score 和 recall_score 方法默认用来计算二分类问题，若要计算多分类问题，则需要设置 average 参数，更多内容请参考官方文档：
precision_score、recall_score

\quad \quad 一般来说，这两者是矛盾的，查准率高时，查全率往往偏低；而查全率高时，查准率往往偏低。通常只有在一些简单任务中才可能使查全率和查准率都很高。

混淆矩阵以及可视化实现

模板：

# 混淆矩阵的可视化显示，以下代码可以直接作为模板
import matplotlib.pyplot as plt
import itertools
import numpy as np
from sklearn.metrics import confusion_matrix
#计算混淆矩阵，confusion_matrix(y_true,y_pred)
cnf_matrix = confusion_matrix(y_true,y_pred)
# 参数：cm:混淆矩阵，classes:数据集目标类别数
def plot_confusion_matrix(cm, classes,
                          title='Confusion matrix',
                          cmap=plt.cm.Blues):
    """
    绘制混淆矩阵
    """
    plt.imshow(cm, interpolation='nearest', cmap=cmap)
    plt.title(title)
    plt.colorbar()
    tick_marks = np.arange(len(classes))
    plt.xticks(tick_marks, classes, rotation=0)
    plt.yticks(tick_marks, classes)

    thresh = cm.max() / 2.
    for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
        plt.text(j, i, cm[i, j],
                 horizontalalignment="center",
                 color="white" if cm[i, j] > thresh else "black")

    plt.tight_layout()
    plt.ylabel('True label')
    plt.xlabel('Predicted label')

应用在鸢尾花数据集上试一试
1、导入数据集

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
# 引入数据集
dataset = load_iris()
data = dataset.data
target = dataset.target
features = dataset.feature_names

# 划分数据集以及模型训练
data_train, data_test, target_train, target_test = train_test_split(data, target, test_size=0.33, random_state=7)
model = DecisionTreeClassifier()
model.fit(data_train, target_train)
# 查看类别数
print(target_train)

结果：

[0 0 2 0 2 1 1 1 0 0 0 1 2 1 1 0 2 0 0 2 2 0 2 0 1 2 1 0 1 0 2 2 1 0 0 1 2
 0 2 2 1 0 1 0 2 2 0 0 2 1 2 2 1 0 0 2 0 0 1 2 2 1 1 0 2 0 0 1 1 2 0 1 1 2
 2 1 2 0 1 1 0 0 0 1 1 0 2 2 1 2 0 2 1 1 0 2 1 2 1 0]

说明鸢尾花类别有0，1，2

2、定义混淆矩阵可视化函数

# 混淆矩阵的可视化显示，以下代码可以直接作为模板
import matplotlib.pyplot as plt
import itertools
import numpy as np
from sklearn.metrics import confusion_matrix
# 参数：cm:混淆矩阵，classes:数据集目标类别数
def plot_confusion_matrix(cm, classes,
                          title='Confusion matrix',
                          cmap=plt.cm.Blues):
    """
    绘制混淆矩阵
    """
    plt.imshow(cm, interpolation='nearest', cmap=cmap)
    plt.title(title)
    plt.colorbar()
    tick_marks = np.arange(len(classes))
    plt.xticks(tick_marks, classes, rotation=0)
    plt.yticks(tick_marks, classes)

    thresh = cm.max() / 2.
    for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
        plt.text(j, i, cm[i, j],
                 horizontalalignment="center",
                 color="white" if cm[i, j] > thresh else "black")

    plt.tight_layout()
    plt.ylabel('True label')
    plt.xlabel('Predicted label')

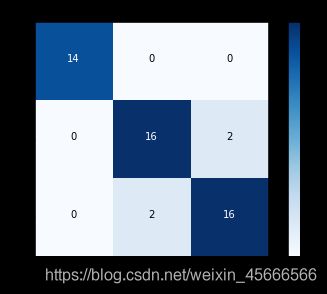
3、计算混淆矩阵并可视化

#计算混淆矩阵，confusion_matrix(y_true,y_pred)
cnf_matrix = confusion_matrix(target_test,model.predict(data_test))
#画出非标准化的混淆矩阵
class_names = [0,1,2]
plt.figure()
plot_confusion_matrix(cnf_matrix,classes=class_names,title='Confusion matrix')
plt.show()

结果：

到此，完工！

【P-R曲线】

\quad \quad 在很多情形下，我们可根据学习器的预测结果对样例进行排序，排在前面的是学习器认为"最可能"是正例的样本，排在最后的则是学习器认为"最不可能"是正例的样本。按此顺序逐个把样本作为正例进行预测，则每次可以计算出当前的查全率、查准率以查准率为纵轴、查全率为横轴作图，就得到了查准率-查全率曲线，简称" P-R 曲线"，显示该曲线的图称为" P-R图"。

\quad \quad 以信息检索为例，刚开始在页面上显示的信息是用户可能最感兴趣的信息，此时查准率高，但只显示了部分数据，所以查全率低。随着用户不断地下拉，信息符合用户兴趣的匹配程度逐渐降低，查准率不断下降，查全率逐渐上升。当下拉到信息底部时，此时的信息是最不符合用户兴趣，因此查准率最低，但所有的信息都已经展示，查全率最高。可以用sklearn.metrics.precision_recall_curve计算PR曲线

需要注意的是 P-R 曲线只能用于二分类问题， 官方文档明确指出：

因此我们需要对鸢尾花数据集进行改造，只取其中两分类。

import numpy as np
from matplotlib import pyplot as plt
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import average_precision_score
from sklearn.svm import LinearSVC
from inspect import signature

iris = load_iris()
X = iris.data
y = iris.target

# 添加噪声
random_state = np.random.RandomState(0)
n_samples, n_features = X.shape
X = np.c_[X, random_state.randn(n_samples, 200 * n_features)]
X_train, X_test, y_train, y_test = train_test_split(X[y < 2], y[y < 2], test_size=.5, random_state=random_state)

# 模型训练
classifier = LinearSVC(random_state=random_state)
classifier.fit(X_train, y_train)
y_score = classifier.decision_function(X_test)
average_precision = average_precision_score(y_test, y_score)
#其中y_test是正确标签，y_score是概率输出值，thresholds是阈值，当y_score>=thresholds，则预测为正样本，当y_score
precision, recall, _ = precision_recall_curve(y_test, y_score)

# 绘制 P-R 图
step_kwargs = ({
     'step': 'post'}
               if 'step' in signature(plt.fill_between).parameters
               else {
     })
plt.step(recall, precision, color='b', alpha=0.2, where='post')
plt.fill_between(recall, precision, alpha=0.2, color='b', **step_kwargs)

plt.xlabel('Recall')
plt.ylabel('Precision')
plt.ylim([0.0, 1.05])
plt.xlim([0.0, 1.0])
plt.title('2-class Precision-Recall curve: AP={0:0.2f}'.format(average_precision))

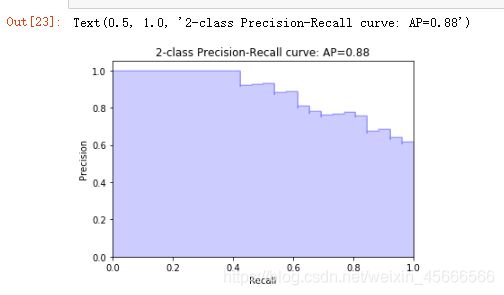
具体代码以及 precision_recall_curve 用法可参考官方文档：

• precision_recall_curve
• 具体代码

P-R 图可以用于学习器的比较：

• 若一个学习器的 P-R 曲线被另一个学习器的 P-R 曲线完全“包住”，则可断言后者的性能优于前者。例如上图中学习器 A 的性能优于学习器 C。
• 若两个学习器的 P-R 曲线发生了交叉，例如学习器 A 与 B，则难以一般性地断言两者孰优孰劣，只能在具体的查准率或查全率条件下进行比较。若要综合性考虑，可使用如下方法。

【交叉时的判断方法】：

• 平衡点（Break-Even Point，简称 BEP）：查准率=查全率时的取值。BEP越大，学习器的性能越好。

  例如图2.3 中学习器C 的BEP 是0 . 64，学习器A的BEP是0.8，学习器B的BEP是0.7而基于BEP的比较，可认为学习器A 优于B 。但BEP 还是过于简化了些，更常用的是F1 度量

• F1 度量：基于查准率与查全率的调和平均（harmonic mean）定义。
  
  F1,是查准率和查全率的调和平均，用于综合考虑这两个性能度量。F1越大，学习器的性能越好。

  有时候我们对查准率，查全率的需求是不同的。比方说广告推荐，要尽量避免打扰用户，因此查准率更重要；而逃犯检索，因为漏检的危害很大，所以查全率更重要。这时就需要使用$F_{\beta }$了，它是F1度量的一般形式，能让我们表达出对查准率/查全率的不同好。

• $F_{\beta }$，是查准率和查全率的加权调和平均，用于综合考虑这两个性能度量，并采用不同的权重。

其中 β>0 度量查全率对查准率的相对重要性，

• β等于1时$F_{\beta }$退化为F1，
• β小于1时查准率更重要，
• β大于1时查全率更重要。

【F1、$F_{\beta }$ 代码实现】

from sklearn.metrics import f1_score
from sklearn.metrics import fbeta_score


# 标准的 F1
print(f1_score(target_test, model.predict(data_test), average='weighted'))
# 输出：0.93995

#  Fβ
print(fbeta_score(target_test, model.predict(data_test), beta=1, average='weighted'))
# 输出：0.93995，可以看到 beta = 1 时，Fb 退化为标准 F1

print(fbeta_score(target_test, model.predict(data_test), beta=2, average='weighted'))
# 输出：0.939859 查全率有更大影响

print(fbeta_score(target_test, model.predict(data_test), beta=0.5, average='weighted'))
# 输出：0.940415 查准率有更大影响

很多时候我们有多个二分类混淆矩阵（鸢尾花数据集就是一个多分类问题，因此上述代码实现中需要添加 average 参数），例如需要进行多次训练/测试，每次得到一个混淆矩阵；或是在多个数据集上进行训练/测试，希望估计算法的“全局”性能，甚或是执行多分类任务，每两两类别的组合都对应一个混淆矩阵。总之，希望在 n 个二分类混淆矩阵上综合考察查准率和查全率。

【做法 1】：
1、在各混淆矩阵上分别计算出查准率和查全率，记为$(P_1,R_1),(P_2,R_2),...,(P_n,R_n)$。
2、计算平均值。
3、得到宏查准率（macro-P）、宏查全率（macro-R）以及相应的宏F1（macro-F1）。

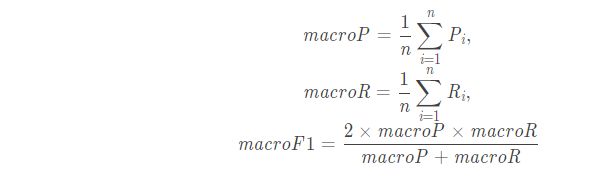
【代码实现】

print(f1_score(target_test, model.predict(data_test), average='macro'))
# 输出：0.9444

【做法 2】：

1、将各混淆矩阵的对应元素进行平均，得到 TP、FP、TN、FN 的平均值，分别记为

2、基于上述平均值计算出微查准率（micro-P）、微查全率（micro-R）和微F1（micro-F1）

print(f1_score(target_test, model.predict(data_test), average='micro'))
# 输出：0.94

关于 F1 和 Fbeta 的更多用法请参考官方文档：

• f1_score
• fbeta_score

3、ROC 与 AUC

\quad \quad 很多学习器是为测试样本产生一个实值或概率预测，然后将这个预测值与一个分类阈值进行比较，若大于阈值则分为正类，否则为反类（如神经网络）。这个实值或概率预测结果的好坏，直接决定了学习器的泛化能力。

\quad \quad 实际上，根据这个实值或概率预测结果，我们可将测试样本进行排序:最可能是正例的排前面，最不能是正例的排后面。这样分类过程就像是在这个序列中以某个截断点（cut point）把样本分成两部分：前一部分判作正例，后一部分则判作反例。我们需要根据任务需求来设置截断点。比如广告推荐更重视查准率，可能就会把截断点设置得更靠前。

在不同的应用任务中，可根据任务需求来采用不同的截断点。

• 若更重视查准率：选择排序中靠前的位置进行截断。
• 若更重视查全率：选择排序中靠后的位置进行截断。

ROC 曲线基于借助排序本身质量好坏来体现综合考虑学习器在不同任务下的“期望泛化性能”的好坏角度出发，研究学习器泛化性能的有力工具。

ROC 全称是“受试者工作特征”（Receiver Operating Characteristic）曲线。根据学习器的预测结果对样例进行排序，按此顺序逐个把样本作为正例进行预测，每次计算出两个重要量的值：假正例率、真正例率，分别以它们为横、纵坐标作图。仍然以二分类混淆矩阵为例：

真实情况	预测结果	预测结果
	正例	反例
正例	TP（真正例）	FN（假反例
反例	FP（假正例）	TN（真反例）

• 纵轴：真正例率（True Positive Rate，简称 TPR）。

  

• 横轴：假正例率（False Positive Rate，简称 FPR）。
  
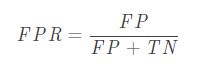
  TPR其实就等于召回率。在绘制ROC曲线时，纵轴为TPR，横轴为FPR。首先按预测值对样本进行排序，然后按序逐个把样本预测为正例，并计算此时的TPR和FPR，然后在图上画出该点，并与前一个点连线。如下图：
  

• 经过 (0,1) 点的曲线，这代表所有正例都在反例之前出现（否则会先出现假正例从而无法经过 (0,1) 点），这是一个理想模型，我们可以设置一个阈值，完美地分割开正例和反例。

• 对角线，这对应于随机猜测模型，可以理解为真正例和假正例轮换出现，即每预测对一次接下来就预测错一次，可以看作是随机猜测的结果。

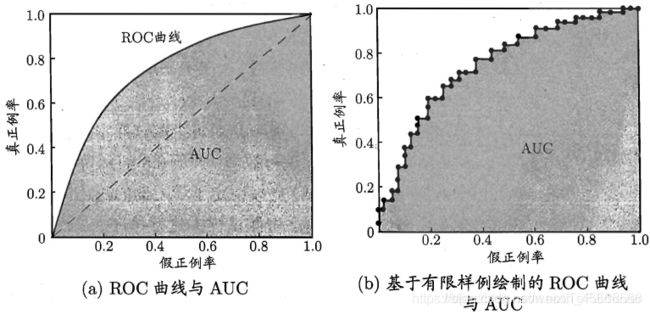
• 现实任务中通常是利用有限个测试样例来绘制 ROC 图，此时仅能获得有限个坐标对，无法产生平滑的 ROC 曲线如图a。

【绘图过程】：给定 $m^{+}$个正例和 $m^{-}$ 个反例，根据学习器预测结果对样例进行排序，然后把分类阈值设为最大，即把所有样例均预测为反例，此时真正例率和假正例率均为 0，在坐标 (0, 0) 处标记一个点，然后，将分类阈值依次设为每个样例的预测值，即依次将每个样例划分为正例。设前一个标记点坐标为 (x, y)，当前若为真正例，则对应标记点的坐标为 $(x,y+\frac{1}{m^{+}})$；若为假正例，则对应标记点的坐标为 $(x+\frac{1}{m^{-}},y)$，然后用线段连接相邻点即得。
如下例：

样本序号	真实标签	预测正类概率	样本序号	真实标签	预测正类概率
1	P	0.9	11	P	0.4
2	P	0.8	12	N	0.39
3	N	0.7	13	P	0.38
4	P	0.6	14	N	0.37
5	P	0.5	15	N	0.36
6	P	0.55	16	N	0.35
7	N	0.54	17	P	0.34
8	N	0.53	18	N	0.33
9	P	0.52	19	P	0.3
10	N	0.51	20	N	0.1

$m^{+}$ = 10，$m^{-}$ = 10，按照绘图过程的步骤，首先将所有样例都预测为反例，则在坐标 (0, 0) 处标记一个点。然后判断第一个样本，将分类阈值设置为当前样本的预测值，即 0.9，同时将该样本当做正例，而恰好当前样本的真实标签是正例，也就是说当前样本属于真正例，那么当前标记点的坐标为 (0, 0 + 1/10) = (0, 0.1)。同理，第二个样本也为真正例，所以坐标为 (0, 0.1 + 1/10) = (0, 0.2)。第三个样本为假正例，故而坐标为 (0 + 1/10, 0.2) = (0.1, 0.2)。依次循环，直到将所有样本的坐标点都计算完毕后，我们根据这些坐标点即可将 ROC 曲线绘制出来，见下图。

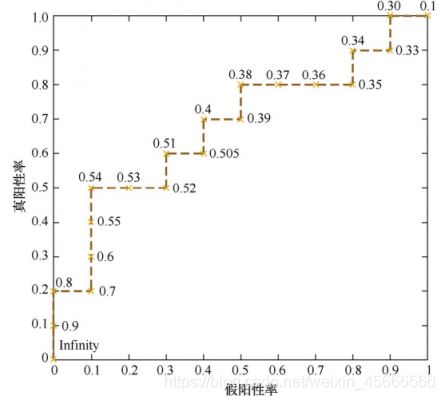
ROC 曲线与 P-R 曲线一样，也可以用来比较不同的学习器：

• 若一个学习器的 ROC 曲线被另一个学习器的曲线完全“包住”，则可断言后者的性能优于前者。
• 若两个学习器的 ROC 曲线发生交叉，则难以一般性地断言两者孰优孰劣。此时如果一定要进行比较，则较为合理的判据是比较 ROC 曲线下的面积，即 AUC（Area Under ROC Curve）。

【AUC】：AUC 指的是 ROC 曲线下的面积大小，该值能够量化地反映基于 ROC 曲线衡量出的模型性能。假定 ROC 曲线是由坐标为 { $(x_1,y_1),(x_2,y_2),...,(x_m,y_m)$} 的点按序连接而形成$(x_1=0,x_m=1)$如图b，则 AUC 可估算为

需要注意的是 roc_curve 同 precision_recall_curve，都只能用于二分类问题，但 sklearn 的 roc_auc_score() 方法支持计算多分类问题的 auc 面积。

关于 auc、roc_curve 以及 roc_auc_score 的用法请参考官方文档：

• auc
• roc_curve
• roc_auc_score

4、代价敏感错误率与代价曲线

现实任务中，有时会遇到不同类型错误造成后果不同的状况。例如在医疗诊断中，错误地把患者诊断为健康人与错误地把健康人诊断为患者，看起来都是犯了"一次错误"但后者的影响是增加了进→步检查的麻烦，前者的后果却可能是丧失了拯救生命的最佳时机；再如，门禁系统错误地把可通行人员拦在门外，将使得用户体验不佳，但错误地把陌生人放进门内，则会造成严重的安全事故。为权衡不同类型错误带来的不同损失，可以为这些错误类型赋以非均等代价（unequal cost）。
以二分类任务为例，可以根据任务的领域知识来设定一个代价矩阵（cost matrix）:

真实类别	预测类别 第0类	第1类
第0类	0	$cos{t}_{01}$
第1类	$cos{t}_{10}$	0

其中，$cos{t}_{ij}$表示将第i类样本预测为第j类样本的代价。
预测值与真实值相等时，自然错误代价为0。但把第0类错预测为第1类和把第1类错预测为第0类这两种错误的代价是不同的。注意，重要的不是代价在数值上的大小，而是它们的比值。比方说
$\frac{cos{t}_{01}}{cos{t}_{10}}>1$, 这就说明把第0类错预测为第1类的代价更高。

使用了非均等代价之后，我们在使用性能度量时自然也需要作出相应的改变，比方说代价敏感（cost-sensitive） 版本的错误率，令$D^{+}$、$D^{-}$分别代表样例集D的正例子集和反例子集，则代价敏感错误率为：

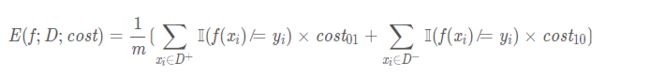
由于ROC曲线不能反应使用非均等代价之后的期望总体代价，所以改用代价曲线（cost curve） 来取替。

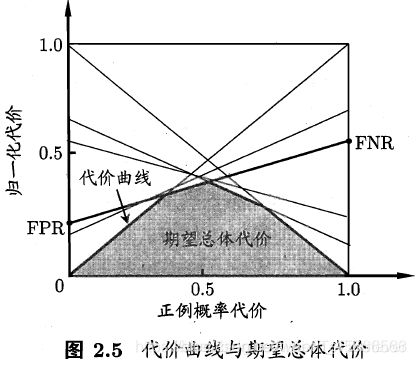
代价曲线图：

横轴是取值为[0,1]的正例概率代价：
$P(+)cost=\frac{p\ast cos{t}_{01}}{p\ast cos{t}_{01}+(1-p)\ast cos{t}_{10}}$

其中p是样例为正例的概率。

纵轴是取值为[0,1]的归一化代价（将代价映射到 [0,1] 区间）

$cos{t}_{norm}=\frac{FNR\ast p\ast cos{t}_{01}+FPR\ast (1-p)\ast cos{t}_{10}}{p\ast cos{t}_{01}+(1-p)\ast cos{t}_{10}}$

其中FPR是假正例率，FNR=1-TPR。

画法类似于ROC曲线，它是将ROC曲线的每一个点转为图中的一条线。依次计算出ROC曲线每个点对应的FPR和FNR，然后把点 (0,FPR) 和点 (1,FNR) 连线。最终所得的图中，所有线的下界所围成的面积就是该模型的期望总体代价。

5、分类报告

\quad \quad scikit-learn 中提供了一个非常方便的工具，可以给出对分类问题的评估报告，Classification_report() 方法能够给出精确率（precision）、召回率（recall）、F1 值（F1-score）和样本数目（support）。

from sklearn.metrics import classification_report


print(classification_report(target_test, model.predict(data_test)))
# 输出：
            precision    recall     f1-score   support

           0       1.00      1.00      1.00        14
           1       0.94      0.89      0.91        18
           2       0.89      0.94      0.92        18

   micro avg       0.94      0.94      0.94        50
   macro avg       0.95      0.94      0.94        50
weighted avg       0.94      0.94      0.94        50

因此，我们在处理多分类问题时，不妨先找一个处理速度最快的模型，然后用分类报告查看一下查准率、查全率、f1 值等信息，以便为后续的优化做一个基准。

总结
\quad \quad 错误率、精度、查准率、查全率、混淆矩阵以及分类报告都可以用于单个模型的性能度量评估，P-R 曲线以及 ROC 也可以用于单个模型的性能度量评估，但更多的是用作多个模型的直观对比。我们把多个模型的 P-R 曲线或 ROC 曲线绘制出来，然后通过上述所讲的比较方法，就可以轻松地选出最优的模型。因此，我个人认为 P-R 曲线和 ROC 曲线一方面是为了查准率和查全率服务，另一面用于多个模型的性能对比。

参考资料：
1、《机器学习》，周志华 著。即西瓜书。
2、南瓜书，是西瓜书的辅助，对西瓜书的一些公式的推导进行进行了一些详解。
3、sklearn 度量官方文档
4、https://blog.csdn.net/weixin_43378396/article/details/90695013