LeetCode刷题笔记——(8/17 - 8/27)
- 2020/8/17:Pow(x, n)、最大子序和 、最多元素
-
- 第一题:pow(x,n):
- 第二题:最大子序和
- 第三题:最多元素
- 2020/8/18:最长回文子串 / 编辑距离
-
- 最长回文子串
- 编辑距离
- 2020/8/19:打家劫舍I/II、最长回文子序列
-
- 打家劫舍
- 最长回文子序列
- 2020/8/20:最长连续递增序列 / 搜索插入位置
-
- 最长连续递增序列
- 搜索插入位置
- 2020/8/25:快乐数、字符出现频率排序、同构字符串
2020/8/17:Pow(x, n)、最大子序和 、最多元素
三道题目都属于分治,分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题,这些子问题相互独立且与原问题性质相同。求出子问题的解,就可得到原问题的解,具体将在下面的题目中体现。
第一题:pow(x,n):
实现 pow(x, n) ,即计算 x 的 n 次幂函数:
示例 1:
输入: 2.00000, 10
输出: 1024.00000
示例 2:
输入: 2.10000, 3
输出: 9.26100
示例 3:
输入: 2.00000, -2
输出: 0.25000
解释: 2-2 = 1/22 = 1/4 = 0.25
说明:
-100.0 < x < 100.0
n 是 32 位有符号整数,其数值范围是 [−231, 231 − 1] 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/powx-n
首先不管什么方法,都要用最快最有效的方式得到答案,其中一个答案对于各种语言都适用,就是直接将题目抄下来加return,因为pow本身就属于math包下的内置函数,含义是计算 x 的 y 次方,在python中,它的使用方式与底层为:
return pow(x, y[, z]) # 写法1,pow(x,y) %z
return x ** y % Z # 写法2
"""
Equivalent to x**y (with two arguments) or x**y % z (with three arguments)
Some types, such as ints, are able to use a more efficient algorithm when
invoked using the three argument form.
"""
但我纠结的是小数点后5位,因为python有比较严重的精度丢失,如果有decimal模块创建数据还好,float很大程度会四舍五入,除非以"%.5f" % L1 用str形式打印内容,但那就不是整数了,但看了下解答发现自己想多了。而想想用第二种思路:分治
x 10 = x ( 1010 ) 2 = x 1 ∗ 2 3 + 0 ∗ 2 2 + 1 ∗ 2 1 + 0 ∗ 2 0 = x 1 ∗ 2 3 ∗ x 0 ∗ 2 2 x 1 ∗ 2 1 ∗ x 0 ∗ 2 0 x^{10}=x^{(1010)_{2}}=x^{1 * 2^{3}+0 * 2^{2}+1 * 2^{1}+0 * 2^{0}}=x^{1 * 2^{3}} * x^{0 * 2^{2}} x^{1 * 2^{1}} * x^{0 * 2^{0}} x10=x(1010)2=x1∗23+0∗22+1∗21+0∗20=x1∗23∗x0∗22x1∗21∗x0∗20
上面式子是通过十进制与二进制数转换来表示幂的乘积,如果上式成立,那么会得到:
x n = { ( x 2 ) n / / 2 , n 为偶数 x ( x 2 ) n / / 2 , n 为奇数 x^{n}=\left\{\begin{array}{ll}\left(x^{2}\right)^{n / / 2} & , n \text { 为偶数 } \\ x\left(x^{2}\right)^{n / / 2} & , n \text { 为奇数 }\end{array}\right. xn={ (x2)n//2x(x2)n//2,n 为偶数 ,n 为奇数
那用 Pow(x, n) (快速幂,清晰图解) 这个题解中的二进制计算中的位运算就能很快得出答案:
class Solution:
def myPow(self, x: float, n: int) -> float:
if x == 0.0: return 0.0
res = 1
if n < 0: x, n = 1 / x, -n
while n:
if n & 1: res *= x
x *= x
n >>= 1
return res
第二题:最大子序和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/maximum-subarray
本题思考的是用动态规划去求解,因为出现了最大和连续与数组等字样,那基本不用想也能用DP求解,那排除掉特殊情况,动态规划的思路为:
- 从第二个数开始循环,取其与前一个数为sum
- 如果 sum > 0,则说明 sum 对结果有增益效果,则 sum 保留并加上当前遍历数字
- 如果 sum <= 0,则说明 sum 对结果无增益效果,需要舍弃,则 sum 直接更新为当前遍历数字
- 遍历结束返回max
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
if not nums:
return 0
elif len(nums) == 1:
return nums[0]
for i in range(1, len(nums)):
# 当前索引i永远存储0~i的最大和
nums[i] = max(nums[i], nums[i] + nums[i - 1])
# 返回每个索引最大和的最大值
return max(nums)
"""
第二种写法
"""
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
if not nums:
return 0
elif len(nums) == 1:
return nums[0]
else:
for i in range(1, len(nums)):
nums[i] = nums[i] + max(nums[i - 1],0)
return max(nums)
另外,看到了有个大佬用了分治,我这里没想到怎么用,也没考虑用,所以这里标记一下:
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
n = len(nums)
#递归终止条件
if n == 1:
return nums[0]
else:
#递归计算左半边最大子序和
max_left = self.maxSubArray(nums[0:len(nums) // 2])
#递归计算右半边最大子序和
max_right = self.maxSubArray(nums[len(nums) // 2:len(nums)])
#计算中间的最大子序和,从右到左计算左边的最大子序和,从左到右计算右边的最大子序和,再相加
max_l = nums[len(nums) // 2 - 1]
tmp = 0
for i in range(len(nums) // 2 - 1, -1, -1):
tmp += nums[i]
max_l = max(tmp, max_l)
max_r = nums[len(nums) // 2]
tmp = 0
for i in range(len(nums) // 2, len(nums)):
tmp += nums[i]
max_r = max(tmp, max_r)
#返回三个中的最大值
return max(max_right,max_left,max_l+max_r)
链接:https://leetcode-cn.com/problems/maximum-subarray/solution/bao-li-qiu-jie-by-pandawakaka/
第三题:最多元素
这题在python里也比较容易,题目太长就直接饮用链接:
https://leetcode-cn.com/problems/majority-element/
这里有很多种解法,可以用hash表做记录然后求最大值,这也是我最直观的一种解法:
class Solution:
def majorityElement(self, nums: List[int]) -> int:
dicts = {
}
for i in nums:
dicts[i] = dicts.get(i,0) + 1
return (max(dicts, key=dicts.get))
第二种可以用python工具类中的counter:
from collections import Counter
class Solution:
def majorityElement(self, nums: List[int]) -> int:
count = Counter(nums)
return count.most_common(1)[0][0]
LeetCode中内置了collections类,因为这是刷题必备的一个工具类,如果在python解释器下,这个包还是需要import。但这个题目最优秀的做法还是从题目意思中体现了:出现次数大于 ⌊ n/2 ⌋ 的元素。也就是说结果要的数,一定是在数组中数量超过1/2,那么就能排序后用中数:
return sorted(nums)[len(nums)//2]
2020/8/18:最长回文子串 / 编辑距离
最长回文子串
最长回文子串我记得很早之前我刷过,知道是用动态规划,然而还是先用暴力来写了,状态方程没有想到,去翻了下很早的博客,思路整理如下:
暴力求解,用队尾元素的删除,让原串来和取反后的进行比较,一旦出现相等的情况,那么就是最大子串:
class Solution:
def longestPalindrome(self, s: str) -> str:
for length in range(len(s), -1, -1):
for index in range(0, len(s) - length + 1):
sub_string = s[index:length + index]
if sub_string == sub_string[::-1]:
return sub_string
另一种解法是对上述的优化,确实强,其主要是把每个字母当成回文串的结束,进行缩放:
class Solution:
def longestPalindrome(self, s: str) -> str:
if not s: return ""
length = len(s)
if length == 1 or s == s[::-1]: return s
max_len,start = 1,0
for i in range(1, length):
even = s[i-max_len:i+1]
odd = s[i-max_len-1:i+1]
if i - max_len - 1 >= 0 and odd == odd[::-1]:
start = i - max_len - 1
max_len += 2
continue
if i - max_len >= 0 and even == even[::-1]:
start = i - max_len
max_len += 1
continue
return s[start:start + max_len]
关于动态规划的解法,首先可以看看求两个字符串的最长公共字串:
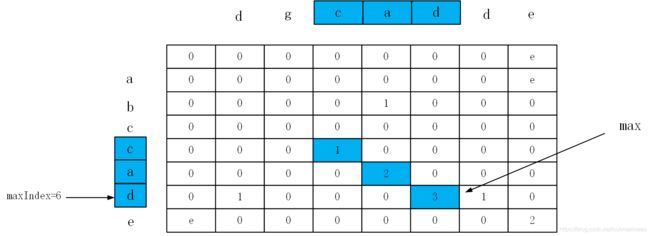
可能有点小丑,但无伤大雅。通过上图所示,max为最长公共子串的长度,以及maxIndex为最长子串结尾字符在字符数组中的位置,由这两个值就可以确定最长公共子串为"cad",实现代码参考python算法面试宝典,如下:
"""
方法功能:获取两个字符串的最长公共字串
输入参数:str1和str2为指向字符的引用(指针)
"""
def getMaxSubStr(str1,str2):
len1 = len(str1)
len2 = len(str2)
SJ = ''
maxs = 0 # 用来记录最长公共子串的长度
maxI = 0 # 用来记录最长公共字串最后一个字符的位置
"""申请新的空间来记录公共字符长度信息"""
M = [[0 for i in range(len1 + 1)] for j in range(len2 + 1)]
"""利用递归公式构建二维数组"""
i,j = 0, 0
"""动态规划推导"""
while i < len1 + 1:
j = 1
while j < len2 + 1:
if list(str1)[i-1] == list(str2)[j-1]:
M[i][j] = M[i-1][j-1] + 1
if M[i][j] > maxs:
maxs = M[i][j]
maxI = i
else:
M[i][j] = 0
j += 1
i += 1
"""找出公共子串"""
i = maxI - maxs
while i < maxI:
SJ = SJ + list(str1)[i]
i += 1
return SJ
而若是求自身的最大子串,参照上面的理解,那么我可以将 J J J变为 S S S的逆序,图解为:
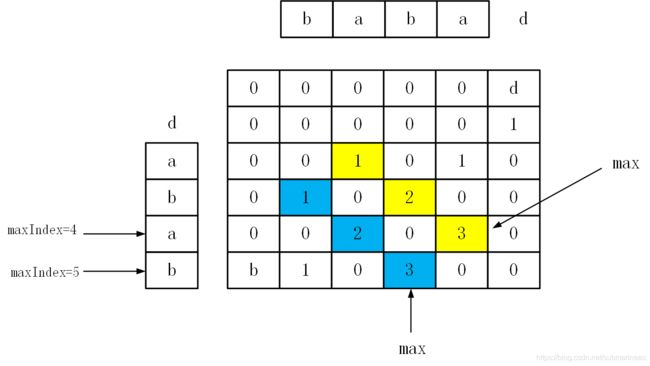
d p [ i ] [ j ] = { true, str [ i ] = = str [ j ] and d p [ i + 1 ] [ j − 1 ] = = tr u e ∣ 1 false d p[i][j]=\left\{\begin{array}{c}\text { true, str }[i]==\operatorname{str}[j] \text { and } d p[i+1][j-1]==\operatorname{tr} u e \mid 1 \\ \text { false }\end{array}\right. dp[i][j]={ true, str [i]==str[j] and dp[i+1][j−1]==true∣1 false
那么代码为:
class Solution:
def longestPalindrome(self, s: str) -> str:
length = len(s)
dp = [[0] * length for _ in range(length)]
left, right = 0, 0 #长度为1时
for i in range(1, length):
for j in range(length-i):
if s[j] == s[j+i] and (j+1 >= j+i-1 or dp[j+1][j+i-1]):
dp[j][j+i] = 1
left, right = j, j+i
return s[left: right+1]
编辑距离
这题并没看懂,然后手边还有其它任务没做完,就先看了下讲解视频,结合官方的文字说明,发现还是对动态规划不熟,如果将删除、编辑和插入都看成是一种状态,确实就简单了。mark一下:
dp[i - 1][j - 1] # 替换,同时前移 i,j
dp[i - 1][j] # 删除,前移i
dp[i][j-1] # 插入,前移j
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
m = len(word1)
n = len(word2)
dp = [[float('inf') for _ in range(n + 1)] for _ in range(m + 1)]
# 初始化
for i in range(m + 1):
dp[i][0] = i
for i in range(n + 1):
dp[0][i] = i
# 状态转移
# i , j 代表 word1, word2 对应位置的 index
for i in range(1, m + 1):
for j in range(1, n + 1):
# 如果word1[:i][-1]==word2[:j][-1],即表示两个的操作最小距离相等,继续向上判断
if word1[i - 1] == word2[j - 1]:
dp[i][j] = dp[i - 1][j - 1]
# 否则从三种状态中选一个最小的然后 +1
else:
dp[i][j] = min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i][j - 1])) + 1
return dp[m][n]
2020/8/19:打家劫舍I/II、最长回文子序列
打家劫舍
打家劫舍I是一个很明显的dp问题,当然也能看做是求奇偶和最大的一方,这两种看起来都没有什么问题,所以代码如下:
class Solution:
def rob(self, nums: List[int]) -> int:
if not nums:
return 0
if len(nums)<=2:
return max(nums)
# 初始状态
dp = [0] * len(nums)
dp[0] = nums[0]
dp[1] = max(nums[0],nums[1])
# dp状态转移方程
for i in range(2,len(nums)):
dp[i] = max(dp[i-1],dp[i-2]+ nums[i])
return dp[-1]
然后打家劫舍II,这题充分暴露了我的短板,我确实想用将打家劫舍I中的两种方法结合起来,判奇偶和动态规划,感觉可以一步到胃,然而确实阵阵胃疼。。。奇数的判断是没问题的,主要是偶数的两个列表,[1,2,3,1] 和 [2,1,1,2]。被卡死了。。。最后发现还是得两遍循环:
class Solution:
def rob(self, nums: List[int]) -> int:
if not nums : return 0
if len(nums) == 1: return nums[0]
def helper(nums):
if not nums : return 0
if len(nums) == 1: return nums[0]
n = len(nums)
dp = [0] * (n + 1)
dp[1] = nums[0]
for i in range(2, n + 1):
dp[i] = max(dp[i - 1], dp[i - 2] + nums[i - 1])
return dp[-1]
return max(helper(nums[1:]), helper(nums[:-1]))
最长回文子序列
被一个bug搞得有点崩,等今晚有时间再完善思路和解法。
现在是第二天晚上,发现今天并不想回看,算了。。
class Solution:
def longestPalindromeSubseq(self, s: str) -> int:
n = len(s)
maxL = -1
dp = [[0]*n for _ in range(n)]
for i in range(n):
dp[i][i] = 1
for i in range(n-1, -1, -1):
for j in range(i+1, n):
if s[i] == s[j]:
dp[i][j] = dp[i+1][j-1] + 2
else:
dp[i][j] = max(dp[i][j-1], dp[i+1][j])
return dp[0][n-1]
2020/8/20:最长连续递增序列 / 搜索插入位置
最长连续递增序列
最简单的一种思路就是对于后一个大于前一个值的序列进行加一,从上面的题刷下来,确实这题一下就写出来了:
class Solution:
def findLengthOfLCIS(self, nums: List[int]) -> int:
n=len(nums)
if not nums or n<0:
return 0
dp=[1]*n
for i in range(1,n):
if nums[i]>nums[i-1]:
dp[i]=dp[i-1]+1
return max(dp)
第二种思路是用单指针的方式,让当前指针永远都指向最大的子序列长度:
class Solution:
def findLengthOfLCIS(self, nums: List[int]) -> int:
if not nums:
return 0
legth = 1
maxleght = 1
for i in range(1,len(nums)):
if nums[i] > nums[i-1]:
legth+= 1
if legth > maxleght:
maxleght = legth
else:
legth = 1
return maxleght
搜索插入位置
// An highlighted block
var foo = 'bar';
2020/8/25:快乐数、字符出现频率排序、同构字符串
可惜今天七夕,这还快乐数?那我快乐就够了,规定找寻50次,如果超过50次还没有变成1,那就是陷入了死循环,返回False
class Solution:
def isHappy(self, n: int) -> bool:
times = 0
while times <= 50:
n = sum([int(i)**2 for i in str(n)])
print(n)
times += 1
if n == 1:
break
return n == 1
同构字符串
class Solution:
def isIsomorphic(self, s: str, t: str) -> bool:
hashmap={
}
for i,j in zip(s,t):
if i in hashmap and hashmap[i]!=j:
return False
elif i not in hashmap and j in hashmap.values():
return False
hashmap[i]=j
return True
根据字符出现频率排序
class Solution:
def frequencySort(self, s: str) -> str:
# Counter
return ''.join([i * j for i, j in collections.Counter(s).most_common()])
