第三周【任务1】学习支持向量机(打卡)

**任务标题：**学习花书5.7.2-5.7.3章，看LDA、SVM两个视频

**任务简介：**学习支持向量机，其他监督学习算法 （视频LDA，SVM）

详细说明：

1.支持向量机

• 对于一个线性可分的数据集，定义样本到分割超平面的最短距离为间隔。间隔越大，分割超平面对两个类别的划分越稳定，不容易受噪声影响。支持向量机的目标即寻找间隔最大的超平面。
• 寻找最大间隔分割超平面可写为一个凸优化问题，根据KKT条件求解。
• 支持向量机的最优决策函数可重写为输入向量与各支持向量的内积求和。用核函数代替内积，可隐式地将样本从原始特征空间映射到更高维的空间，解决原始特征空间中的线性不可分问题。
• 常见的核函数包括高斯核，又称radial basis function (RBF)核。

2. LDA

• 理解类间方差和类内方差，LDA损失函数

学习目标：

a. 监督学习：SVM，LDA

b.了解支持向量机的动机

c. 掌握支持向量机算法

d.了解如何通过核函数解决线性不可分问题

e.理解LDA与PCA的不同

打卡内容：

问题一：

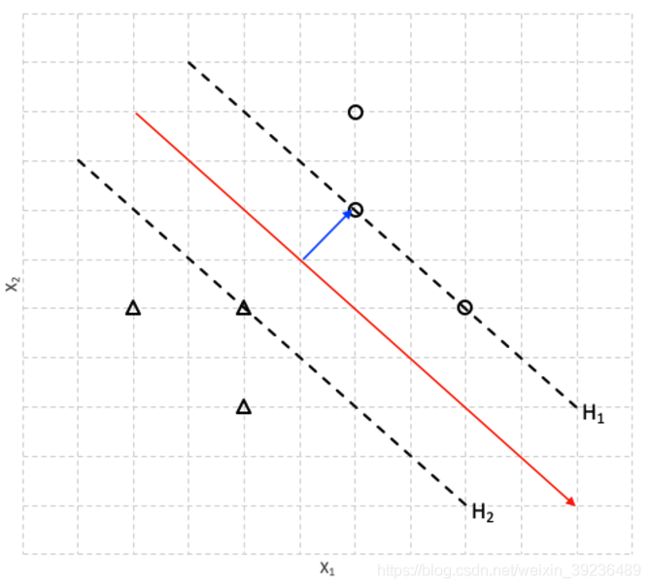
假设我们要学习一个硬间隔SVM， 其线性决策函数为${\mathbf{w}}^{\top }\mathbf{x}+b=0$. 输入特征为$x_1,x_2$，标签$y\in \{-1,+1\}$

分别用$△$和$\circ$表示。如图

1. 根据最大间隔原则，在图中标出支持向量，并大致画出对应的分割超平面。

2. 若超平面$H_1$的表达式是${\mathbf{w}}^{\top }\mathbf{x}+b=1$,写出超平面$H_2$表达式

$${\mathbf{w}}^{\top }\mathbf{x}+b=-1$$

3.线性硬间隔支持向量机的限制可以写作$y_i\left({\mathbf{w}}^{\top }{\mathbf{x}}_{\mathbf{i}}+b\right)\ge 1,\forall i\in \{1,\dots ,N\}$，解释其原因

首先我们设点$x_0$到超平面的距离为$r$，在超平面上的投影为$x_1$， 那么法向量$w$一定与向量${\mathbf{x}}_1{\mathbf{x}}_0$平行，此时若考虑求两个向量内积的绝对值可得
$$\left|{\mathbf{w}}^{\mathrm{T}}\cdot {\mathbf{x}}_1{\mathbf{x}}_0\right|=\Vert \mathbf{w}\Vert \cdot |\pm 1|\cdot \Vert {\mathbf{x}}_1{\mathbf{x}}_0\Vert =\Vert \mathbf{w}\Vert \cdot r$$
又因为
$$\begin{array}{rl}{\mathbf{w}}^{\mathrm{T}}\cdot {\mathbf{x}}_1{\mathbf{x}}_0& =w_1\left(x_0^1-x_1^1\right)+w_2\left(x_0^2-x_1^2\right)+\dots +w_n\left(x_0^n-x_1^n\right)\\ & =w_1{x}_0^1+w_2{x}_0^2+\dots +w_n{x}_0^n-\left(w_1{x}_1^1+w_2{x}_1^2+\dots +w_n{x}_1^n\right)\\ & =w_1{x}_0^1+w_2{x}_0^2+\dots +w_n{x}_0^n-(-b)\\ & =w_1{x}_0^1+w_2{x}_0^2+\dots +w_n{x}_0^n+b={\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_0+b\end{array}$$
【可以理解${\mathbf{x}}_0$这个从坐标原点为起点的向量先投影在法向量$\mathbf{w}$上，然后减去$b$这个原点到超平面的距离，就得到了${\mathbf{x}}_1{\mathbf{x}}_0$在法向量上的投影长度】

所以
$$\begin{gathered} \left|{\mathbf{w}}^{\mathrm{T}}\cdot \overline{{\mathbf{x}}_1{\mathbf{x}}_0}\right|=\left|{\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_0+b\right|=\Vert \mathbf{w}\Vert \cdot r \\ \Rightarrow r=\frac{\left|{\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b\right|}{\Vert \mathbf{w}\Vert } \end{gathered}$$
我们又定义函数间隔：给定数据集$D=\left\{\left({\mathbf{x}}_1,y_1\right)\cdot \left({\mathbf{x}}_2,y_2\right)\dots \left({\mathbf{x}}_m\cdot y_m\right)\right\},y_i\in \{-1,+1\}$和超平面${\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b=0$,定义超平面关于样本$\left({\mathbf{x}}_i,y_i\right)$的函数间隔为
$${\hat{\gamma }}_i=y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)$$
定义超平面关于数据集的间隔函数为超平面关于数据集中所有样本的函数间隔最小值，也就是
$$\hat{\gamma }=\underset{1,2,\dots ,m}{\min }{\hat{\gamma }}_i$$
定义几何间隔：定义超平面关于样本$\left({\mathbf{x}}_i,y_i\right)$的几何间隔为
$${\gamma }_i=\frac{{\hat{\gamma }}_i}{\Vert \mathbf{w}\Vert }$$
同样，定义超平面关于数据集的几何间隔为超平面关于数据集中所有样本的几何间隔最小值，也就是
$$\gamma =\underset{1,2,\dots ,m}{\min }{\gamma }_i=\frac{\hat{\gamma }}{\Vert \mathbf{w}\Vert }$$
SVM的核心思想：求一个与已知数据集几何间隔最大的那个超平面，也就是
$$\begin{array}{ll}\min & \gamma \\ \text{ s.t. }& {\gamma }_i\ge \gamma ,i=1,2,\dots ,m\\ \min & \frac{\hat{\gamma }}{\Vert \mathbf{w}\Vert }\\ \text{ s.t. }& \frac{{\gamma }_i}{\Vert \mathbf{w}\Vert }\ge \frac{\hat{\gamma }}{\Vert \mathbf{w}\Vert },i=1,2,\dots ,m\\ \min & \frac{\hat{\gamma }}{\Vert \mathbf{w}\Vert }\\ \text{ s.t. }& y_i\left(\mathbf{w}{\mathbf{x}}_i+b\right)\ge \hat{\gamma },i=1,2,\dots ,m\\ \min & \frac{1}{\Vert \mathbf{w}\Vert }\\ \text{ s.t. }& y_i\left(\mathbf{w}{\mathbf{x}}_i+b\right)\ge 1,i=1,2,\dots ,m\\ {\min }_{\mathbf{w},b}& \frac{1}{2}\Vert \mathbf{w}{\Vert }^2\\ \text{ s.t. }& 1-y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)⩽0,i=1,2,\dots ,m\end{array}$$
这就是可以写作$y_i\left({\mathbf{w}}^{\top }{\mathbf{x}}_{\mathbf{i}}+b\right)\ge 1$的原因，$y_i$为样本类别$\{-1,1\}$，对于分类正确的正样本$\left(w^{T} x_{i}+b\right) \geq 1 $且$ y_{i}=1$，对于分类正确的负样本$\left(w^{T} x_{i}+b\right) \leq-1$且$y_i=-1$.

4.当训练集数据满足什么要求时，存在一个可行的$\mathbf{w}$？

能够正确划分训练数据集并且几何间隔最大。间隔最大化：不仅将正负实例点分开，而且对最难分离的实例点也有足够大的确信度将他们分开

5.推导超平面$H_1$和$H_2$间距离（间隔）的表达式

如果两个点$x_1$和$x_2$分别在$H_1$和$H_2$上，那么两个点到超平面的距离为
$$\begin{gathered} r_1=\frac{\left|{\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_1+b\right|}{\Vert \mathbf{w}\Vert }=\frac{1}{\Vert \mathbf{w}\Vert } \\ {r}_2=\frac{\left|{\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_2+b\right|}{\Vert \mathbf{w}\Vert }=\frac{1}{\Vert \mathbf{w}\Vert } \end{gathered}$$
所以两个超平面间的距离间隔表达式是
$$\frac{2}{\Vert \mathbf{w}\Vert }$$

6.根据以上问题的答案，写出对应硬间隔支持向量机的优化问题的表达式

满足硬约束条件
$$\begin{array}{ll}{\min }_{\mathbf{w},b}& \frac{1}{2}\Vert \mathbf{w}{\Vert }^2\\ \text{ s.t. }& 1-y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)⩽0,i=1,2,\dots ,m\end{array}$$

7.对于以下数据点${\mathbf{x}}_1=(1,2,3),{\mathbf{x}}_2=(4,1,2),{\mathbf{x}}_3=(-1,2,-1)$及其对应标签$=y_1=+1,y_2=+1,y_3=-1$，正确的SVM决策函数${\mathbf{w}}^{\top }\mathbf{x}+b=0$为以下某一选项。找出该选项

$$\begin{array}{l}\text{ 1. }\mathbf{w}=[0.3,0,0.4{]}^{\top },b=-0.4\\ \text{ 2. }\mathbf{w}=[0.2,0,0.4{]}^{\top },b=-0.4\\ \text{ 3. }\mathbf{w}=[0.1,0,0.4{]}^{\top },b=-0.4\\ \text{ 4. }\mathbf{w}=[0.4,0,0.2{]}^{\top },b=-0.4\end{array}$$

正确的是选项2，因为选项2的w与三个点相乘的结果是[1, 1.2, -1]正分类最小值1，负分类最大值-1，且$w^2$相加值最小。

问题二: 从最优化理论的角度解释为什么存在支持向量

在满足KKT条件的情况下，对于任意训练样本$\left({\mathbf{x}}_i,y_i\right)$, 总有${\alpha }_i=0$或者$y_{i}f\left({\mathbf{x}}_i\right)=1$.如果${\alpha }_i=0$，则该样本将不会在$f(\mathbf{x})$中的求和出现，也就不会对$f(\mathbf{x})$有任何影响。如果${\alpha }_i>0$，则必有$f(\mathbf{x})$,所对应的样本点位于最大间隔边界上，是一个支持向量。因此KKT条件保证了支持向量的存在

问题三：为什么svm核函数不需要知道核函数的具体形式，只要知道内积的表达式

因为特征空间维数可能很高，甚至无穷维，因此直接计算$\varphi {\left({\mathbf{x}}_i\right)}^{\mathrm{T}}\varphi \left({\mathbf{x}}_j\right)$非常困难，我们有了核函数$\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=⟨\varphi \left({\mathbf{x}}_i\right),\varphi \left({\mathbf{x}}_j\right)⟩=\varphi {\left({\mathbf{x}}_i\right)}^{\mathrm{T}}\varphi \left({\mathbf{x}}_j\right)$后，${\mathbf{x}}_{\mathbf{i}}$与${\mathbf{x}}_{\mathbf{j}}$在特征空间的内积等于他们在原始样本空间中通过函数$\kappa (\cdot ,\cdot )$计算的结果。这样，我们就不必直接计算高位特征空间中的内积。

如果我们回顾XOR异或问题，我们知道，不可能找到一个线性表达式超平面$y=wx+b$进行划分。我们会把x做一个非线性变换$x\to \varphi (x)$，我们不需要知道变换函数的表达式。但是对任意两个样本${\mathbf{x}}_1,{\mathbf{x}}_2$，我们需要知道他们的内积$\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=⟨\varphi \left({\mathbf{x}}_i\right),\varphi \left({\mathbf{x}}_j\right)⟩$. 我们试想有另外一个样本${\mathbf{x}}_3$， 那么做了非线性变换后$\varphi ({\mathbf{x}}_3)$, 有$w\varphi ({\mathbf{x}}_3)+b$. 看上去似乎要继续知道$\varphi$的表达式才行.

我们通过拉格朗日对偶的方法，可以让权重变成$\omega ={\sum }_i{\lambda }_i{\mathbf{x}}_{\mathbf{i}}{y}_i$, 这里$i$是遍历训练中的所有样本, $\lambda$就是拉格朗日系数。加了核函数之后$\omega ={\sum }_i{\lambda }_i\varphi ({\mathbf{x}}_{\mathbf{i}})y_i$. 然后把系数矩阵代回去，就有$f={\sum }_i{\lambda }_i\varphi \left({\mathbf{x}}_{\mathbf{i}}\right)\varphi \left({\mathbf{x}}_3\right)y_i+b$ . 显然，我们只要知道任意两个样本做非线性变换后做的内积结果就足够了。

问题四：自己独立推导svm算法

问题五：查资料说明svm的优缺点

优点

• 可以解决高维问题，即大型特征空间；
• 能解决小样本下机器学习问题；
• 能够处理非线性特征的相互作用；
• 无局部极小值问题；（相对于神经网络等算法）
• 无需依赖整个数据；
• 泛化能力比较强；

缺点

• 时间复杂度高，当观测样本很多时，效率并不是很高；
• 对非线性问题没有通用解决方案，有时候很难找到一个合适的核函数；
• 对于核函数的高维映射解释力不强，尤其是径向基函数；
• 常规SVM只支持二分类；
• 对缺失数据敏感；

问题六：说出LDA与PCA的区别

1. PCA最小重构误差，使得投影后的值和原来的值尽量接近，属于非监督学习
2. LDA最大化类间距离，最小化类内距离，使得投影后的不同类别的样本分的更开， 属于监督学习