吴恩达机器学习课程笔记——Ch5 多元线性回归
Chapeter 5 Linear Regression with Multiple Variables（多元线性回归）
终于改成看一节视频做一节笔记了 == 否则视频1小时，笔记3小时的操作真心蛋疼...
课程笔记总览传送门：https://blog.csdn.net/weixin_42900928/article/details/86523192
Chapeter 5 Linear Regression with Multiple Variables（多元线性回归）
5.1 Multiple Features（多维特征、多元、多变量）
5.2 Gradient descent for multiple varialbes（多变量梯度下降）
5.3 Feature Scaling (特征缩放)
5.4 Learning Rate（学习率）
5.5 Features and Polynomial Regression（特征和多项式回归）
5.6 Normal Equation（正规方程）
其它
5.1 Multiple Features（多维特征、多元、多变量）
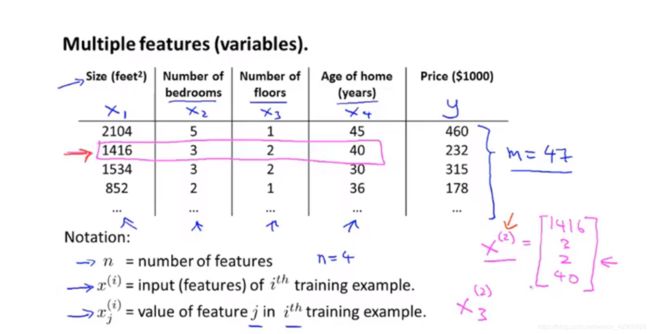
第二章用一元起了个头，这章应该就开始了。加了几个自变量（特征）后，从一元变成了多元。根据图1-1， 回归方程就变成了：
图 1-1 符号标定
第一喜欢的符号解释环节：
m —— 样本数，第一章有提到；
n —— 特征数量,或者结合线代和后续操作，可以称为特征维数；
—— 表示第 i 个实例，是特征矩阵的第 i 行，需要注意的是，他是一个向量（vector）；
—— 特征矩阵中第 i 行第 j 列的特征。
如：
由图1-1，m=47,n=4；
![x^{(2)}=[1416,3,2,40]^{T}](http://img.e-com-net.com/image/info8/2e503acaf34a43a887191976881694f3.gif){kind=small}
； 
。
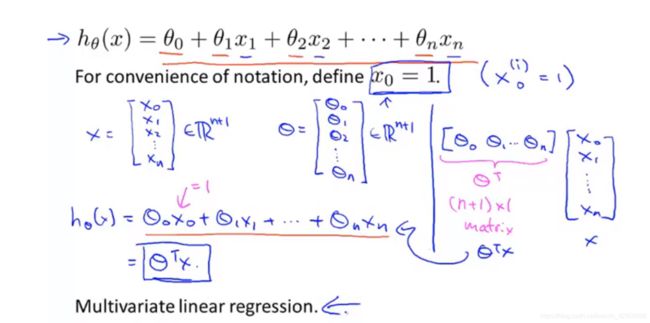
更一般地，多元回归方程写为：
图 1-2 多元回归方程代数和矩阵表达式
需要注意的是，引入了 
,它的存在是为了方便后续与特征矩阵 
的互动，大家都是（n+1）* 1 的矩阵，这样转个置就可以相乘，得到如下的表达式：
![h_{\theta}(x)=\theta_{0}x_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+...+\theta_{n}x_{n}=\theta^{T}x=[\theta_{0},\theta_{1},\theta_{2},...,\theta_{n}][x_{0},x_{1},x_{2},...,x_{n}]^{T}](http://img.e-com-net.com/image/info8/0d8b7d9393774e07a7f7d84189c08160.gif){kind=small}
而这，就是多元线性回归。
5.2 Gradient descent for multiple varialbes（多变量梯度下降）
上一节已经对公式的形式进行了改变，这一节将会进一步改变公式的形式，并且解释多变量梯度下降和单变量的联系和不同。
图 2-1
由图 2-1 可知，拥有线代概念是十分重要的，把 
统一变成了 ，把 
变成了 
，这大大减少了公式长度。
接下来，看一下一元变成多元后，梯度下降的算法怎么样了：
图 2-2 新老梯度下降对比
左边，一元；右边，多元。有3个点：
（1）目的都是一样的，找出代价函数 （这里已经用 了，很简便yo）的最小值，使得误差最小，模型最精确；
（2） 
，y 也同理，下标 j 代表是第几个特征变量，第一节提过；
（3）紫框和蓝框都代表一样的算法，说明即便变成了多元， 
和 
的梯度下降公式依旧不变。因此，在对多元感到困惑时，可以从一元的梯度下降公式入手找感觉。
5.3 Feature Scaling (特征缩放)
先来看一个对比：
图 3-1 不同特征取值的比较
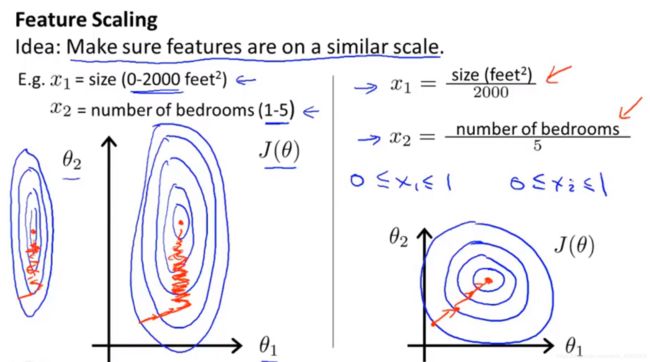
图 3-1 中：
左图，2个特征，一个取值范围很大（0~2000），一个取值范围很小（1~5），图像很瘦长。这会怎么样呢？梯度下降的慢且会艰辛，就像橘色标记所示。
右图，2个特征，取值范围都是（0，1），图像很圆润。这会怎么样呢？梯度下降的快且稳。
值得注意的是：都除以了它们的最大值。
这种操作的目的是，让特征的取值范围尽可能一样，从而快速收敛。
那么，在什么范围内比较好呢？
图 3-2 范围的选择
图 3-2 很清晰的展示了一系列的取值范围，打√的是比较好的，打×的是不太行的，当然，这只是他觉得的，当然，最好跟着他觉得的来。
最后，最实用最普遍最简单的方法：
图 3-3 标准化
标....标准化 ？！你怎么到这里来了 =.=
这一节就是在说怎么对数据进行一些简单的处理（方法），让它收敛的更快（目的）。
方法很重要，永远要记住目的。
5.4 Learning Rate（学习率）
本节说了怎么选学习率。
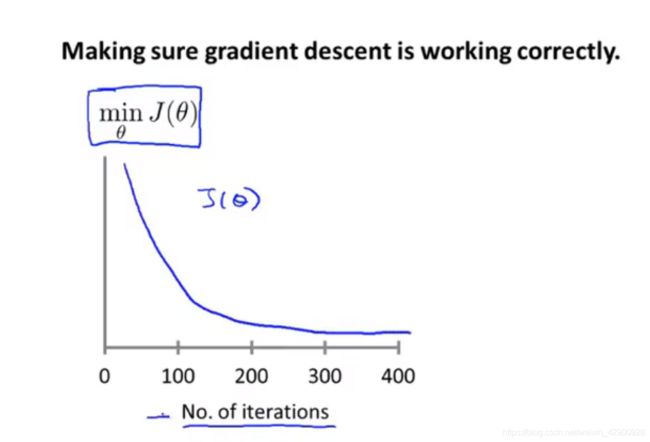
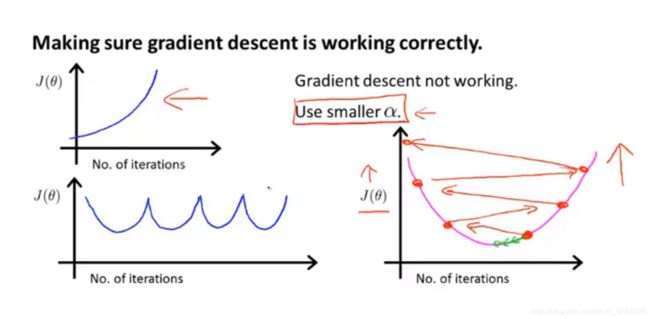
首先，理想学习率make的函数-迭代次数曲线应该是这样的：
图 4-1 代价函数-迭代次数曲线
即稳步下降。终于看到这个图了（哟吼~），以前觉得很酷...这是比较好用来观察是否收敛的方式，比如400以后几乎不怎么变了，则可以认为其收敛。当然，也有一些自动判敛的阈值之类的，但嗯哒老师说这个不怎么靠谱，因为不同情况需要的阈值是不同的。
那么，当 
过大时，会出现如下情况：
图 4-2 学习率过大时的图像
看到你的图这样了，就把学习率调低一点把，没错，这就算是调参了（哟吼~调参可太酷了）。
那么，有什么设置学习率的套路呢。你好，有的：
图 4-3 学习率取值示意图
如图4-3。
别忘了目的：保证梯度是下降的，然后在梯度下降的过程中加快收敛，然后得到自己想要的低误差模型。
5.5 Features and Polynomial Regression（特征和多项式回归）
本节说了怎么选取特征，以及用线性回归的方式对多项式回归进行拟合（表达不行，意思到位即可，对不对另说）
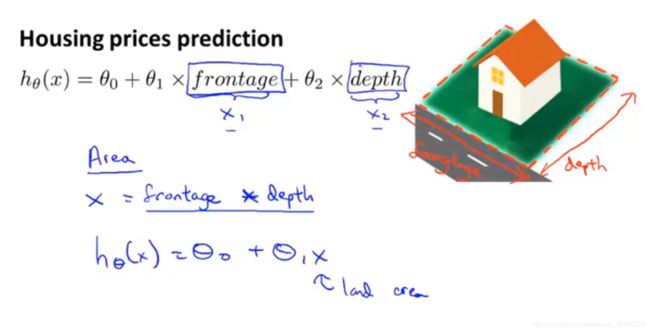
第1个例子：
图 5-1 合并特征
一开始有2个特征：长和宽（你看这面....它又长又...），但可以直接用面积来替代。
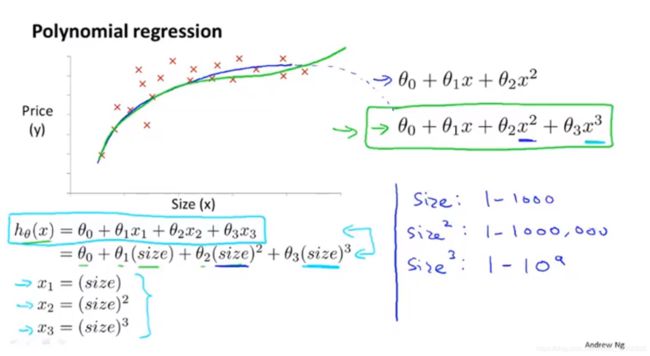
第2个例子：
图 5-2 用线性回归拟合多项式回归
这个就厉害了，这图像明显直线拟合的效果不太好，用曲线会好一些，那么怎么用线性回归来替代呢？可以替换特征，如图 5-2 ，当然要注意取值范围的问题，就像之前讲的，要操作一下。
PS：我要早点看到这节，我那大作业可怜的拟合度是不是会好点。
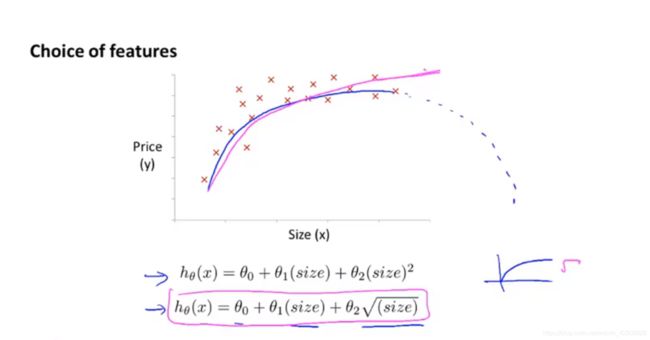
第3个例子：
图 5-3 换换换
想用曲线拟合，但第一个图像会降，不符合现实，怎么办？换特征！
这一节真的很重要了，虽然短。特征的选取无论对模型拟合度还是对实际价值都有无比的意义，提供了几个思路，归纳一下就是变变变，需要仔细参悟。
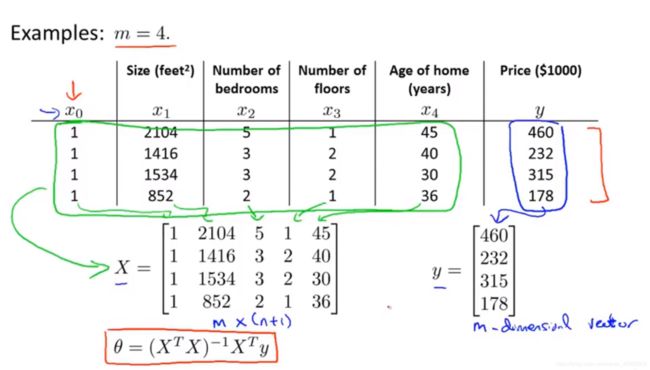
5.6 Normal Equation（正规方程）
本节讲了一个可以不用迭代就可以直接取得最小 （矩阵！！！！）的方法——正规方程。
梯度下降啥都好，就是要迭代，要调参（学习率），那有没有一下子出结果的？你好，有的。
图 6-1 正规方程的操作
如图， 一下子就出来了....而且它就是最小值。而且用正规方程完全不用考虑特征取值范围是否一致啊、合理啊（也就是4.3提的）...
这里的X又称design matrix设计矩阵。
那么，它无敌了吗？吊打梯度下降了吗？没有。
图 6-2 梯度下降和正规方程的比较
图 6-2 告诉我们，在特征没有很多的情况下（100、1000、<10000），正规方程很棒。但特征超过10000甚至更大时，特征方程计算矩阵花的时间就太多了，可以考虑梯度下降了。另外就是，在后续一些复杂算法如逻辑回归这样的，不能用正规方程求解，所以梯度下降依旧能打。
其它
加了个 ，从零开始的异世界回归方程 #_# 总感觉计算机气息浓厚...
我这个排版可是越来越能看了，哈哈啊哈。今天编辑公式的时候发现有个“compressed”按钮，看介绍挺??，什么可以更好地嵌入啥的，然而后续完全不能改，那几个最长的公式都是手打出来的（崩溃?）。
然后加了个传送门，方便看看别的章节，万一能火呢（小声bb）