子带分解

子带分解与合成

在语音信号处理中，通常使用STFT对信号进行分频带处理，，STFT公式表示如下
$$Y(m,w)=\sum _{n=-\infty }^{+\infty }x(t)w(t-mD)e^{-jwt}$$
STFT过程可以表示为使用一个滑动窗相乘然后做DFT，在STFT中，窗函数的长度通常与频域点数（子带数）相等，但是频域分辨率又与输入数据的长度有关，这个时候，可以用Filter bank的视角来理解 ¹STFT的过程。

在子带处理过程中，通常使用更长的分析窗，这样能使各个子带之间的相关性更小，在一些自适应滤波的任务中通常能有更快的收敛速率，而通过一些分解综合设计手段，能够最大程度抵消掉混叠现象完美恢复（Perfect Reconstruction ）信号.

1. 卷积和DFT

在STFT的第$m$帧中，加窗-DFT过程表示如下
$$Y({\omega }_k)=\sum _{n=0}^{N-1}x(mD-n)h(n)e^{-j{\omega }_{k}n}$$
而对比卷积公式如下
$$y(t)=\sum _{n=0}^{N-1}x(t-n)h(n)$$
可以看到，STFT中的加窗傅里叶变换过程可以看做将信号$x(n)$与$h(n)e^{-j{\omega }_{k}n}$的滤波器做卷积，而$h(n)e^{-j{\omega }_{k}n}$又可以看做是将滤波器$h(n)$进行复调制（移频）得到的另外一个滤波器，因此DFT过程可以看做是将信号$x(n)$经过一组带通滤波器组进行卷积滤波的过程，

2. DFT filter bank

上面讲到可以将低通滤波器进行复调制得到带通滤波器，表示如下
$$h_i(n)=p(n)e^{j\ast 2\ast \pi /N\ast n},i=0,1,....N-1$$
其中N表示 DFT点数，也是子带个数，matlab代码如下

N = 16;   % 子带数
L = 128;   %滤波器长度
hopt = fir1(L-1,1/N)';

H = zeros(L,N/2+1);
n=[0:L-1]';
for k = 0:1:(N/2-1)
    H(:,k+1) = hopt.*exp(j*2*pi/N*k*n); % Complex modulation
end

nfft = 16384;           % only for better visualization
mag = fft(H,nfft);
mag = mag(1:nfft/2+1,:);
figure,plot((1:nfft/2+1)/nfft*2*pi,10*log10(abs(mag)));
xlabel('normalized frequency'),ylabel('gain/dB');
ylim([-60,10]);

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-OPRamvf2-1609341511333)(E:\work\matlab\Github\subband\doc\mag.png)]

3.子带分解

3.1 子带分解示例

一个典型的子带分解与合成的过程如下图所示²

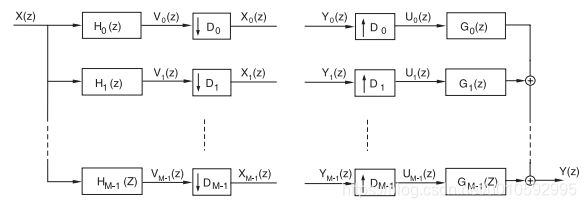
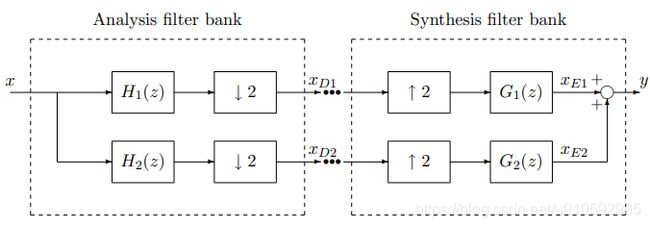
其中$H(z)$为分析滤波器，$G(z)$为综合滤波器，$D$为重采样因子，$X_k$可以看做独立的低速率子带信号，$X_k$和$Y_k$之间可以进行自适应滤波或者噪声谱估计等操作。

举例分两个子带过程如下³

$H_1(z)$为低通滤波器，通带为[0,$\pi /2$]，$H_2(z)$为高通滤波器，通带为[$\pi /2,\pi$]，子带分解和合成可以按以下步骤进行

• 子带分解：

1. 设计一个原型低通滤波器(prototype filter)，然后进行复调制得到各个通带滤波器
2. 将输入信号$x$分别与各个子带滤波器进行卷积滤波，得到调制后各个子带信号
3. 将各个子带信号进行抽取（下采样），如上图上的2个子带，则滤波之后每隔一个点取一个

• 子带综合：

1. 将各子带信号$x_D$进行上采样，如上图中的2个子带，则每两个点之间插入一个0

2. 将各个升采样后的子带信号与综合滤波器进行卷积滤波，得到解调后的子带信号

3. 将各个子带信号相加，得到最终合成后的全带信号

这个过程的可以用文末的matlab代码演示，注意，这里合成后的信号并不等于输入信号，即不满足PR(perfect reconstruction)条件¹，PR可以表示为下式，表示输出仅是输入的一个延时以及常数K倍的关系
$$y(n)=Kx(n-\Delta )$$
若满足PR条件，需要各个子带滤波器的频谱overlap-add后为一个常数，这也与STFT 的PR条件¹中需要窗函数满足COLA条件相对应。

3.2 高效计算

​ 上图中的子带处理过程可以进一步优化，上图中的分析与综合滤波器滤波都是在高采样率端进行的，看分析端，每新到一个采样点都进行一次卷积运算，但是后面的抽取过程会丢弃一个点，表明每两次卷积运算就有一次是无用的，因此可以将抽取和滤波调换位置，先进行下采样抽取，再进行卷积滤波。后面的综合过程也是同样的道理，可以将插值和滤波调换位置，让滤波操作在低速率端进行。

图示如下

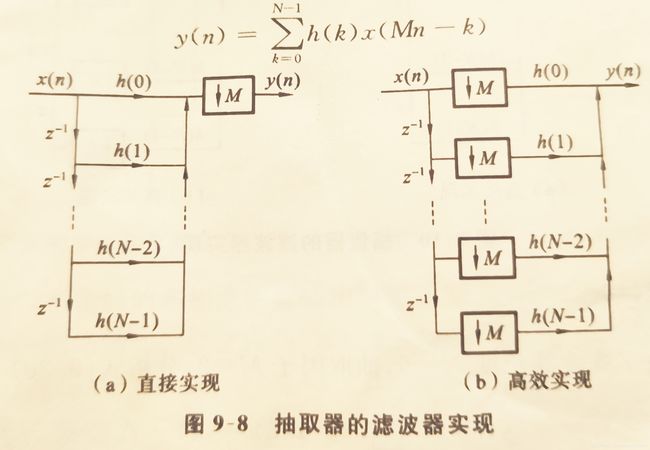
​ 另外，原型滤波器经过复调制再与信号卷积滤波的过程可以通过DFT高效计算，

另外，子带分解综合过程可以通过多相滤波进一步高效计算，这个过程用公式表示如下⁴
$$X_k(m)=\sum _{n=0}^{L-1}x(mD-n)h(n)e^{-j\ast 2\ast \pi \ast k/M\ast n}$$
其中$L$为分析窗长，$M$为子带个数，通常为了FFT计算选为2的整数次幂$D$为抽取因子，通常$D\le M<L$，注意这里的FFT点数$M$与$窗长L$不相等，而通常STFT中$M=L$。

3.3 混叠

子带滤波虽然使用了更长的分析窗，能够得到更陡峭的过渡带以及更小的阻带衰减，但是依然不可能达到理想滤波器的效果。因此子带间会有混叠现象，如果不进行其它操作，这个混叠能过通过设计一些分析综合滤波器（QMF）来相互抵消掉，从而依旧能完美复原信号⁵。但是这个混叠只是在首尾被抵消掉了，而在各个子带中还是存在，这样就依旧会影响到各个子带中的处理过程，比如，针对各个子带自适应滤波器的收敛会变慢。

在实际使用中，通常使用oversampled 来降低aliasing的影响。

上面讲到子带处理过程通过调换滤波和重采样过程可以提高计算效率，而抽取的过程对应着实际使用过程中的hop_size/shift/抽取因子D，例如当子带数$M=256$，如果hop_size=M​，则为critical sampled ，如实际常用的hop_size=M/2，则为oversampled 。oversampled 的形式能有更小的混叠效应。

code

close all

%%
N = 2;                                % number of band
L = 16384;                            %prototype lowpass filter length

hopt = fir1(L-1,[1e-12 0.5])';        % prototype lowpass filter [0,pi/2]

H = zeros(L,N);
n=[0:L-1]';
for k = 0:1:N-1
    H(:,k+1) = hopt.*exp(1i*2*pi/N*k*n); % Complex modulation
end
G = zeros(size(H));
G(:,1) = 2*(H(:,1));
G(:,2) = 2*H(:,2);

nfft = 16384;                             % only for better visualization
mag = fft(H,nfft);
mag = mag(1:nfft/2+1,:);
figure,plot((1:nfft/2+1)/nfft*2*pi/pi,10*log10(abs(mag)));
xlabel('normalized frequency'),ylabel('gain/dB');
ylim([-60,10]);
% % FreqResp
figure,plot((1:nfft/2+1)/nfft*2*pi/pi,10*log10(sum(abs(mag).^2,2)))
title('gian error')

%%
[x,fs] = audioread('../cleanspeech.wav');

x1_lowpassed = conv(x,H(:,1));                 % convolution filtering
x1_highpassed = conv(x,H(:,2));

xd1 = x1_lowpassed(1:2:end);                   % decimation
xd2 = x1_highpassed(1:2:end);

xe1 = zeros(length(xd1)*2,1);
xe2 = zeros(length(xd1)*2,1);

xe1(1:2:end) = xd1;                            % interpolation
xe2(1:2:end) = xd2;

xe1 = conv(xe1,G(:,1));                        % demodulation
xe2 = conv(xe2,G(:,2));

y = xe1 + xe2;
y = real(y);
[rxy,lags] = xcorr(x,y);
[ma,index] = max(rxy);
lags(index)                        % +lag indicate x1 is behind of x2
                                   % -lag indicate x1 is ahead of x2
pt(x)
y = real(y(16382:end));
y = y(1:length(x));

pt(x-y(1:length(x)))

Reference:

---

1. https://www.dsprelated.com/freebooks/sasp/Filter_Bank_Summation_FBS.html ↩︎ ↩︎ ↩︎

2. filter bank design for subband adaptive filtering. ↩︎

3. Multirate digital signal processing ↩︎

4. [Efficient FIR Filtering for Decimation (binghamton.edu)](http://www.ws.binghamton.edu/fowler/fowler personal page/EE521_files/IV-08 Uniform DFT Filter Bank_2007.pdf) ↩︎

5. Subband adaptive filtering theory and implementation,chapter 2,P48 ↩︎