基于自适应滤波器和小波分析的奇异值分解图像压缩(MATLAB实现)
基于自适应滤波器和小波分析的奇异值分解图像压缩
摘要
根据奇异值分解的数学原理和矩阵特点,设计基于奇异值分解的图像压缩算法,探索算法的图像压缩效果。同时针对设计出来的奇异值分解的图像压缩算法进行性能分析与研究,发现可以通过自适应中值滤波进行图像优化,增强图像的视觉清晰度;还可以在对图像进行小波变换,从而进行图像频域提取,达到小波分解的效果。利用小波分解后的图像数据再进行基于奇异值分解的图像压缩,大大改善了图像的压缩性能。
自适应滤波、小波分解、奇异值分解的原理
自适应滤波器:
由于滤波器开发者的设计思路不同,可在自适应滤波器中运用的算法有很多种,目前使用较多的算法有最小均方误差法和递推最小二乘法。本次实验中主要使用递推最小二乘法。
递推最小二乘法的基本原理是尽可能每时每刻都对输入有用的数据重估所得到的平法误差的加权总和尽可能的小,取得最优化的最小值。这一点就使得递推最小二乘法在数字图像处理的精确程度上要优于最小均方误差算法,其收敛性得到了大幅度的提升,最终图像质量也得到了显著提升。但是,递推最小二乘法也同样存在一些不足之处,优于递推最小二乘法的运算较为繁琐,使得其运算量大幅度的增加,数字图像的处理速度降低,处理所需要的时间大大增加,这就在一定程度上降低了自适应滤波器的数字图像处理效率,且滤波器阶数较大时,递推最小二乘法的运算难以得到期望结果。递推最小二乘法的运算过程以来数据总体的样本数,样本数越多,计算结果约为精确,但是,当样本数不足时,将难以得到最优化的结果。
小波分解:
小波变换具有多尺度分析能力,可以将图像分解到不同分辨率上进行处理。图像经小波变换后,每一分辨率的小波系数均由一个低频子代(LL)和水平(LH)、垂直(HL)和对角(HH)3个方向的高频子代组成。小波分解只对低频子代进行再分解而保持高频子代不变,因此图像经过J层小波分解后,会产生3J+1个子代,不同子代表示图像不同频率信息,如下图所示:
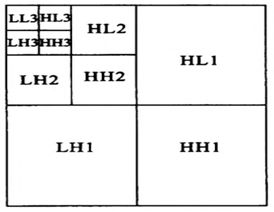
奇异值分解
奇异值分解(SVD)是线性代数中一种重要的矩阵分解,奇异值分解则是特征分解在任意矩阵的推广。矩阵的奇异值分解变换是一种正交变换,它可以将矩阵对角化。
MATLAB代码实现
RAMF函数(自适应中值滤波函数):
function f = RAMF(img) %RAMF函数(自适应中值滤波函数):
[Im,In] = size(img);
nmin = 3;
nmax = 9;
Imf = img;
I_ex = [zeros((nmax-1)/2,In+(nmax-1));zeros(Im,(nmax-1)/2),img,zeros(Im,(nmax-1)/2);zeros((nmax-1)/2,In+(nmax-1))];
for x = 1:Im
for y = 1:In
for n = nmin:2:nmax
Sxy = I_ex(x+(nmax-1)/2-(n-1)/2:x+(nmax-1)/2+(n-1)/2,y+(nmax-1)/2-(n-1)/2:y+(nmax-1)/2+(n-1)/2);
Smax = max(max(Sxy));%求出窗口内像素的最大值
Smin = min(min(Sxy));%求出窗口内像素的最小值
Smed = median(median(Sxy));%求出窗口内像素的中值
%判断中值是否是噪声点
if Smed > Smin && Smed < Smax
%若中值既大于最小值又小于最大值,则不是
%是,则退出该if语句,增大窗口尺寸,再次判断
%不是,则判断该点的原值是不是噪声点
if Imf(x,y) <= Smin || Imf(x,y) >= Smax
%若该点的原值既大于最小值又小于最大值,则不是
%不是,则输出原值,即不作处理
%是,则输出中值
Imf(x,y) = Smed;
end
break%有输出则不再进行循环判断
end
end
%当n=max时,输出中值
Imf(x,y) = Smed;
end
end
f = Imf;
end
wave_aly函数(两层小波分解函数):
function [img1,img2] = wave_aly(X) %2层小波分解函数
%对图像用小波进行2层小波分解
[c,s]=wavedec2(X,10,'bior3.7');
%进行图像压缩
%保留小波分解第一层低频信息
%首先对第一层信息进行量化编码
ca1=appcoef2(c,s,'bior3.7',1);
ca1=wcodemat(ca1,440,'mat',0);
%改变图像高度
img1 = 0.5*ca1;
figure();
image(img1);
title("保留小波分解第一层低频信息的小波分解图像");
%保留小波分解第二层低频信息进行压缩
ca2=appcoef2(c,s,'bior3.7',2);
%首先对第二层信息进行量化编码
ca2=wcodemat(ca2,440,'mat',0);
%改变图像高度并显示
img2 = 0.25*ca2;
figure();
image(img2);
title("保留小波分解第二层低频信息的小波分解图像");
end
SVD_Compression函数(基于奇异值分解的图像压缩函数):
function [img,D,compress_ratio] = SVD_Compression(k,I)
%构建基于奇异值分解的图像压缩函数
%k代表保留的奇异值个数,I代表输入的图像数据
if (size(I,3) ~= 1) %判断输入的图像的数据是否为三维数值数组
I = rgb2gray(I); %三维数值数组转换维二维灰度值
end
I = double(I); %转换为可进行奇异值分解的double类型数组
[U D V] = svd(I); %进行奇异值分解,I=U*D*V
[m,n] = size(I); %图像大小
I_rank = rank(I); %输入图像矩阵的秩
if k <= I_rank
img = uint8(U(:,1:k)*D(1:k,1:k)*V(:,1:k)'); %保留前k个奇异值,进行图像压缩
else
fprintf('输入的保留的奇异值个数k大于输入图像矩阵I的秩%d,无法进行图像压缩',I_rank);
img = I;
end
%计算图像压缩比
I_elements = m*n;
compress_elements = m*k + k*k + k*n;
compress_ratio = I_elements/compress_elements;
end
直接对原图像进行奇异值分解压缩:
clear all
clc
k = 1:10:101; %保留的奇异值数组
n = length(k); %保留的奇异值数组大小
compress_ratio = zeros(1,n); %构造压缩比数组
I = imread('Lenna.png');
figure();
imshow(I);
title('原图像');
for i = 1:n
%自定义奇异值压缩函数SVD_Compression,进行奇异值压缩
[img,D,ratio] = SVD_Compression(k(i),I);
compress_ratio(i) = ratio;
figure();
imshow(img);
title_str = ['保留前',int2str(k(i)),'奇异值的图像'];
title(title_str)
end
disp("直接对原图像进行压缩的压缩比:");
disp(compress_ratio);
%绘制奇异值的分布曲线
figure();
plot(diag(D),'b-','LineWidth',3);
title('输入原图像矩阵的奇异值分布');
ylabel('奇异值大小');
xlabel('奇异值所在奇异值矩阵D中的位置');
%绘制绘制奇异值个数与压缩比的关系曲线
figure();
plot(k,compress_ratio,'b-','LineWidth',3);
title('直接对原图像进行压缩的奇异值个数与压缩比的关系');
xlabel('奇异值个数');
ylabel('压缩比');
输入原图像自适应中值滤波后的奇异值分解压缩:
clear all
clc
I = imread('Lenna.png');
%自定义自适应中值滤波RAMF,对输入图像进行自适应中值滤波进行奇异值压缩
I = RAMF(I);
k = 1:10:101; %保留的奇异值数组
n = length(k); %保留的奇异值数组大小
compress_ratio = zeros(1,n); %构造压缩比数组
figure();
imshow(I);
title('原图像自适应中值滤波后的图像');
for i = 1:n
%自定义奇异值压缩函数SVD_Compression,进行奇异值压缩
[img,D,ratio] = SVD_Compression(k(i),I);
compress_ratio(i) = ratio;
figure();
imshow(img);
title_str = ['自适应中值滤波后保留前',int2str(k(i)),'奇异值'];
title(title_str)
end
disp("自适应中值滤波后的图像进行压缩的压缩比:");
disp(compress_ratio);
%绘制奇异值的分布曲线
figure();
plot(diag(D),'b-','LineWidth',3);
title('自适应中值滤波后矩阵的奇异值分布');
ylabel('奇异值大小');
xlabel('奇异值所在奇异值矩阵D中的位置');
%绘制绘制奇异值个数与压缩比的关系曲线
figure();
plot(k,compress_ratio,'b-','LineWidth',3);
title('自适应中值滤波后的奇异值个数与压缩比的关系');
xlabel('奇异值个数');
ylabel('压缩比');
输入原图像自适应中值滤波和小波分解后的奇异值分解压缩:
clear all
clc
I = imread('Lenna.png');
%自定义自适应中值滤波RAMF,对输入图像进行自适应中值滤波进行奇异值压缩
I = RAMF(I); %对输入图像进行自适应中值滤波
%自定义两层小波分解函数wave_aly,对输入图像进行两层小波分解
[img1,img2] = wave_aly(I);
n_img1 = length(img1); %图像img1大小
n_img2 = length(img2); %图像img2大小
k1 = 1:10:101; %保留的奇异值数组
n1 = length(k1); %保留的奇异值数组大小
compress_ratio_1 = zeros(1,n1); %构造压缩比数组
%保留小波分解第一层低频信息的图像进行奇异值分解
for i = 1:n1
%自定义奇异值压缩函数SVD_Compression,进行奇异值压缩
[img_one,D1,ratio] = SVD_Compression(k1(i),img1); %进行奇异值压缩
compress_ratio_1(i) = ratio;
figure();
imshow(img_one);
title_str = ['保留第一层低频信息的前',int2str(k1(i)),'奇异值'];
title(title_str)
end
compress_ratio_1 = compress_ratio_1.*((316/n_img1)^2); %图像压缩比
disp("自适应中值滤波和保留小波分解第一层低频信息后的图像进行压缩的压缩比:");
disp(compress_ratio_1);
%绘制奇异值的分布曲线
figure();
plot(diag(D1),'b-','LineWidth',3);
title('自适应中值滤波和保留小波分解第一层低频信息后矩阵的奇异值分布');
ylabel('奇异值大小');
xlabel('奇异值所在奇异值矩阵D中的位置');
%绘制绘制奇异值个数与压缩比的关系曲线
figure();
plot(k1,compress_ratio_1,'b-','LineWidth',3);
title('自适应中值滤波和保留小波分解第一层低频信息后的奇异值个数与压缩比的关系');
xlabel('奇异值个数');
ylabel('压缩比');
%保留小波分解第二层低频信息的图像进行奇异值分解
k2 = 1:10:81;
n2 = length(k2);
compress_ratio_2 = zeros(1,n2); %构造压缩比数组
for j = 1:n2
%自定义奇异值压缩函数SVD_Compression,进行奇异值压缩
[img_two,D2,ratio] = SVD_Compression(k2(j),img2); %进行奇异值压缩
compress_ratio_2(j) = ratio;
figure();
imshow(img_two);
title_str = ['第二层低频信息的前',int2str(k2(j)),'奇异值'];
title(title_str)
end
compress_ratio_2 = compress_ratio_2.*((316/n_img2)^2); %图像压缩比
disp("自适应中值滤波和保留小波分解第二层低频信息后的图像进行压缩的压缩比:");
disp(compress_ratio_2);
%绘制奇异值的分布曲线
figure();
plot(diag(D2),'b-','LineWidth',3);
title('自适应中值滤波和保留小波分解第二层低频信息后矩阵的奇异值分布');
ylabel('奇异值大小');
xlabel('奇异值所在奇异值矩阵D中的位置');
%绘制绘制奇异值个数与压缩比的关系曲线
figure();
plot(k2,compress_ratio_2,'b-','LineWidth',3);
title('自适应中值滤波和保留小波分解第二层低频信息后的奇异值个数与压缩比的关系');
xlabel('奇异值个数');
ylabel('压缩比');