python 数据分析 numpy 矩阵与数组基本运算
一、 numpy矩阵
numpy:计算模块;主要有两种数据类型:数组、矩阵
特点:运算块
[]+[]
import numpy as np
1、numpy创建矩阵
mat1=np.mat('1 2 3;2 3 4;1 2 3')
mat1
matrix([[1, 2, 3],
[2, 3, 4],
[1, 2, 3]])
type(mat1)
numpy.matrix
mat2=np.mat('0 2;22 48;30 12')
mat2
matrix([[ 0, 2],
[22, 48],
[30, 12]])
print(mat2)
[[ 0 2]
[22 48]
[30 12]]
mat3=np.mat('1 2 2;2 2 4;1 1 2')
print(mat3)
[[1 2 2]
[2 2 4]
[1 1 2]]
2.矩阵计算
print('矩阵加法运算:\n',mat1+mat3)
矩阵加法运算:
[[2 4 5]
[4 5 8]
[2 3 5]]
print('矩阵乘法运算:\n',mat1*mat2)
矩阵乘法运算:
[[134 134]
[186 196]
[134 134]]
print('矩阵的转置:\n',mat1.T)
矩阵的转置:
[[1 2 1]
[2 3 2]
[3 4 3]]
mat4=np.mat('1 0 0;0 4 0;0 0 6')
print('逆矩阵:\n',mat4.I)
逆矩阵:
[[1. 0. 0. ]
[0. 0.25 0. ]
[0. 0. 0.16666667]]
print('矩阵的数乘:\n',4*mat4)
矩阵的数乘:
[[ 4 0 0]
[ 0 16 0]
[ 0 0 24]]
print('矩阵对应元素相乘的运算:\n',np.multiply(mat1,mat3))
矩阵对应元素相乘的运算:
[[ 1 4 6]
[ 4 6 16]
[ 1 2 6]]
print('矩阵乘法:\n',mat1*mat3)
矩阵乘法:
[[ 8 9 16]
[12 14 24]
[ 8 9 16]]
2 矩阵属性
print('矩阵的结构:\n',mat1.shape)
矩阵的结构:
(3, 3)
print('矩阵元素个数:\n',mat1.size)
矩阵元素个数:
9
print('矩阵元素类型:\n',mat1.dtype)
矩阵元素类型:
int32
print('矩阵的维度:\n',mat1.ndim)
矩阵的维度:
2
三、数组的创建
数据的所有运算都是对应元素的运算;
1.数组的创建
# 一维数组
arr1=np.array([1,2,3,4])
print(arr1)
[1 2 3 4]
print(type(arr1))
# 二维数组:
arr2=np.array([[1,2,3],[0,1,2],[2,3,1]])
print(arr2)
[[1 2 3]
[0 1 2]
[2 3 1]]
# 列向量类型的数组:
arr3=np.array([[1],[2],[3],[4]])
print(arr3)
[[1]
[2]
[3]
[4]]
2 数组的属性
print('一维数组结构:\n',arr1.shape)
一维数组结构:
(4,)
print('二维数组结构:\n',arr2.shape)
二维数组结构:
(3, 3)
print(arr3.shape)
(4, 1)
print('数组的元素个数:\n',arr1.size)
print('数组的元素个数:\n',arr2.size)
数组的元素个数:
4
数组的元素个数:
9
print('一维元素的类型:\n',arr1.dtype)
print('二维元素类型:\n',arr2.dtype)
一维元素的类型:
int32
二维元素类型:
int32
print('一维数组的维度:\n',arr1.ndim)
print('二维数组的维度:\n',arr2.ndim)
print('二维数组的维度:\n',arr3.ndim)
一维数组的维度:
1
二维数组的维度:
2
二维数组的维度:
2
3.数组的索引
# 一维数组的索引:
arr1[::-1]
array([4, 3, 2, 1])
# 二维数组的切片:
print(arr2)
# arr2[行切片,列切片]
arr2[1,2]
arr2[::2,::2]
[[1 2 3]
[0 1 2]
[2 3 1]]
array([[1, 3],
[2, 1]])
arr2[1:3,1:3]
array([[1, 2],
[3, 1]])
arr2[:2,::2]
array([[1, 3],
[0, 2]])
# 不同行不同列的切片
arr2[(1,0,1),(0,1,2)]
array([0, 2, 2])
arr2[(2,1,0),(0,1,2)]
array([2, 1, 3])
# bool取值:不要行列同时传入bool值,
mask=np.array([1,0,1],dtype=np.bool)
print(mask)
[ True False True]
arr5=np.array([1,6,3,4,5])
mask=np.array([0,1,0,1,1],dtype=np.bool)
arr5[mask]
array([6, 4, 5])
4 特殊函数创建数组
(1) arange类似于range
arr6=np.arange(1,10,1)
print(arr6)
[1 2 3 4 5 6 7 8 9]
(2) 等差数列:
np.linspace(start=a1, stop=an, num=50, endpoint=True, retstep=False, dtype=None, axis=0)
参数说明:
endpoint=True: 表示等差数列, 在start与stop之间插入 n-2 个值;(n为数值的个数)
endpoint=False: 表示等差数列, 在start与stop之间插入 n-1个值,表示平均分成n份;(为线段的个数)
arr7=np.linspace(8,2,7)
print(arr7)
[8. 7. 6. 5. 4. 3. 2.]
参数说明:
endpoint=True:表示等差数列,在start和stop之间插入n-2个值
print(np.logspace(1,3,3))
[10 100 1000]
默认base=10 就是以10为底,首位10的1次幂,末位10的3次幂,共3个数
arr8=np.logspace(1,10,10,base=2)
print(arr8)
[ 2. 4. 8. 16. 32. 64. 128. 256. 512. 1024.]
base=2 是以2为底,指数从1开始,指数到10结束,十个数
a1=2=2**1
q=2 -->base=2
n=10
a10=2*2**(10-1)=2**10
例题:a1=3 q=9 n=6
arr9=np.logspace(1,11,6,base=3)
print(arr9)
[3.00000e+00 2.70000e+01 2.43000e+02 2.18700e+03 1.96830e+04 1.77147e+05]
以3为底,首位3的1次幂,末位3的11次幂共6个数
另一种解法
```python
print(np.logspace(0.5,5.5,6,base=9))
[3.00000e+00 2.70000e+01 2.43000e+02 2.18700e+03 1.96830e+04 1.77147e+05]
a1=3=9^0.5
a6=3*9^(6-1)=9^0.5*9^5=9^5.5
例题:a1=2 q=3 n=5
print(np.logspace(np.log10(2),np.log10(2*(3**4)),5))
mat6=np.mat('1 0 0;0 2 0;0 0 3')
print(mat6)
[[1 0 0]
[0 2 0]
[0 0 3]]
print(mat6.I)
[[1. 0. 0. ]
[0. 0.5 0. ]
[0. 0. 0.33333333]]
mat7=np.mat('4 0 0;0 5 0;0 0 6')
print(mat7)
[[4 0 0]
[0 5 0]
[0 0 6]]
print(mat6**6)
[[ 1 0 0]
[ 0 64 0]
[ 0 0 729]]
print(mat6+mat7)
[[5 0 0]
[0 7 0]
[0 0 9]]
print(mat6-mat7)
[[-3 0 0]
[ 0 -3 0]
[ 0 0 -3]]
a=np.mat('0 3 3;1 1 0;-1 2 3')
e=np.mat('1 0 0;0 1 0;0 0 1')
c=a-2*e
print(c)
[[-2 3 3]
[ 1 -1 0]
[-1 2 1]]
print(c.I)
[[-0.5 1.5 1.5]
[-0.5 0.5 1.5]
[ 0.5 0.5 -0.5]]
b=a*c.I
print(b)
[[ 0. 3. 3.]
[-1. 2. 3.]
[ 1. 1. 0.]]
mat8=np.mat('1 2 3;2 2 5;3 5 1')
mat9=np.mat('1;2;3')
print(mat8)
print(mat9)
print(mat8.I)
[[1 2 3]
[2 2 5]
[3 5 1]]
[[1]
[2]
[3]]
[[-1.53333333 0.86666667 0.26666667]
[ 0.86666667 -0.53333333 0.06666667]
[ 0.26666667 0.06666667 -0.13333333]]
x=mat8.I*mat9
print(x)
[[1.00000000e+00]
[5.55111512e-17]
[1.11022302e-16]]
mat11=np.mat('1 1 1;1 2 4;1 3 9')
mat12=np.mat('2 ;3 ;5')
print(mat11)
print(mat12)
[[1 1 1]
[1 2 4]
[1 3 9]]
[[2]
[3]
[5]]
print(mat11.I)
[[ 3. -3. 1. ]
[-2.5 4. -1.5]
[ 0.5 -1. 0.5]]
print(mat11.I*mat12)
[[ 2. ]
[-0.5]
[ 0.5]]
(4)全一数组
arr9 = np.ones((3, 4))
print(arr9)
[[1. 1. 1. 1.]
[1. 1. 1. 1.]
[1. 1. 1. 1.]]
(5) 全零数组
arr10 = np.zeros((3,3))
print(arr10)
[[0. 0. 0.]
[0. 0. 0.]
[0. 0. 0.]]
(6)单位数组
arr11 = np.eye(3)
print(arr11)
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]
(7)对角数组
arr12 = np.diag([1, 2, 3, 4])
print(arr12)
[[1 0 0 0]
[0 2 0 0]
[0 0 3 0]
[0 0 0 4]]
5.创建随机数组:
(1) 创建n个在0~1之间的随机数, 为一维数组
arr13 =np.random.random(10)
print(arr13)
[0.39707333 0.01181148 0.44722191 0.34679938 0.15179949 0.91379825
0.50060085 0.40059831 0.93092686 0.34490374]
(2) 创建服从均匀分布的随机数组
arr14 = np.random.rand(1000)
import matplotlib.pyplot as plt
plt.figure()
plt.hist(arr14, 10)
plt.show()
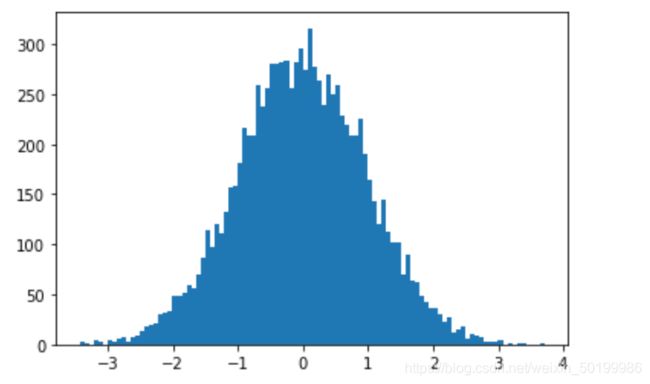
(3) 创建正态分布数组随机数
arr15 = np.random.randn(10000)
import matplotlib.pyplot as plt
plt.figure()
plt.hist(arr15, 100)
plt.show()
(4) 随机整数的生成
low <= x < high
np.random.randint(2, 4, size=[2, 5])
array([[2, 2, 3, 3, 2],
[3, 3, 2, 2, 2]])
6.矩阵形态变换
(1) 重置数组结构:
a、一维变二维
arr_1 = np.arange(10)
print(arr_1)
[0 1 2 3 4 5 6 7 8 9]
arr_2 = arr_1.reshape((2, 5))
print(arr_2)
[[0 1 2 3 4]
[5 6 7 8 9]]
b.展平: 二维变一维
arr_2.ravel()
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
c、展平方法二:flatten
order=‘C’:表示横向展平; order='F’表示纵向展平;
arr_2.flatten('C')
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
arr_2.flatten('F')
array([0, 5, 1, 6, 2, 7, 3, 8, 4, 9])
d、堆叠方法
arr_3 = np.zeros((3, 4))
arr_4 = np.ones((3, 4))
横向堆叠: 行数一样即可;
arr_5 = np.hstack((arr_3, arr_4))
print(arr_5)
[[0. 0. 0. 0. 1. 1. 1. 1.]
[0. 0. 0. 0. 1. 1. 1. 1.]
[0. 0. 0. 0. 1. 1. 1. 1.]]
纵向堆叠: 列数相同
arr_6 = np.vstack((arr_3, arr_4))
print(arr_6)
[[0. 0. 0. 0.]
[0. 0. 0. 0.]
[0. 0. 0. 0.]
[1. 1. 1. 1.]
[1. 1. 1. 1.]
[1. 1. 1. 1.]]
e:数组合并 concatenate
arr_i = np.concatenate((arr_3, arr_4), axis=0) #沿着axis=0的方向进行拼接
print(arr_i)
[[0. 0. 0. 0.]
[0. 0. 0. 0.]
[0. 0. 0. 0.]
[1. 1. 1. 1.]
[1. 1. 1. 1.]
[1. 1. 1. 1.]]
arr = np.concatenate((arr_3, arr_4), axis=1) # 沿着axis=1轴的方向进行拼接
print(arr)
[[0. 0. 0. 0. 1. 1. 1. 1.]
[0. 0. 0. 0. 1. 1. 1. 1.]
[0. 0. 0. 0. 1. 1. 1. 1.]]
ar_1 = np.array([1,2,3,4])
ar_2 = np.array([0,1,2,2])
concatenate与hstack/vstack的区别:
concatenate是严格沿着数组的轴的方向拼接的,一维数组只有一个轴,因此只有一个种拼接方式;
hstack/vstack 不关注有几个轴,只是单纯按照纵向或横向方向堆叠即可,因此一维数组也有两种堆叠方式;
np.concatenate((ar_1, ar_2), axis=0)
array([1, 2, 3, 4, 0, 1, 2, 2])
np.vstack((ar_1, ar_2))
array([[1, 2, 3, 4],
[0, 1, 2, 2]])
f.数组分割
#横向分割
np.hsplit(arr, 4 )
[array([[0., 0.],
[0., 0.],
[0., 0.]]), array([[0., 0.],
[0., 0.],
[0., 0.]]), array([[1., 1.],
[1., 1.],
[1., 1.]]), array([[1., 1.],
[1., 1.],
[1., 1.]])]
# 任意分割的方法:列索引取值 :2, 2:4, 4:7, 7:
np.hsplit(arr, np.array([2, 4, 7]))
[array([[0., 0.],
[0., 0.],
[0., 0.]]), array([[0., 0.],
[0., 0.],
[0., 0.]]), array([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]]), array([[1.],
[1.],
[1.]])]
np.vsplit(arr_i,3 )
[array([[0., 0., 0., 0.],
[0., 0., 0., 0.]]), array([[0., 0., 0., 0.],
[1., 1., 1., 1.]]), array([[1., 1., 1., 1.],
[1., 1., 1., 1.]])]
np.split(arr_i,2, axis=1 ) # 沿着轴的分割;
[array([[0., 0.],
[0., 0.],
[0., 0.],
[1., 1.],
[1., 1.],
[1., 1.]]), array([[0., 0.],
[0., 0.],
[0., 0.],
[1., 1.],
[1., 1.],
[1., 1.]])]
- 数组运算
(1)四则运算:+ - * / ** %
arr17 = np.arange(1, 17).reshape((4,4))
print(arr17)
[[ 1 2 3 4]
[ 5 6 7 8]
[ 9 10 11 12]
[13 14 15 16]]
arr18 = np.diag([2, 3, 1, 5])
print(arr18)
[[2 0 0 0]
[0 3 0 0]
[0 0 1 0]
[0 0 0 5]]
arr18 % arr17
array([[0, 0, 0, 0],
[0, 3, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 5]], dtype=int32)
(2)比较运算: >, <, == <= >= !=
print(arr18 < arr17)
[[False True True True]
[ True True True True]
[ True True True True]
[ True True True True]]
mask = arr17 > 8
print(mask)
[[False False False False]
[False False False False]
[ True True True True]
[ True True True True]]
arr17[mask]
array([ 9, 10, 11, 12, 13, 14, 15, 16])
(3) 逻辑运算
a、逻辑与运算:
np.all(mask)
False
b、逻辑或运算:
np.any(mask)
True
(4) 数组广播运算
a、二维数组+ 列向量
arr_19 = np.array([[1], [0], [1], [0]])
print(arr_19)
[[1]
[0]
[1]
[0]]
print(arr17+ arr_19)
[[ 2 3 4 5]
[ 5 6 7 8]
[10 11 12 13]
[13 14 15 16]]
b、二维数组+ 行向量
arr20 = np.array([0,1,0,1])
print(arr17+arr20)
[[ 1 3 3 5]
[ 5 7 7 9]
[ 9 11 11 13]
[13 15 15 17]]
print(arr17 > 8 )
[[ 9 10 11 12]
[13 14 15 16]
[17 18 19 20]
[21 22 23 24]]
(5)特殊方法
a、排序的方法
sort排序,并修改原始数组无返回值
arr21=np.array([21,10,20,8,15,1])
print(arr21)
arr21.sort()
print(arr21)
[21 10 20 8 15 1]
[ 1 8 10 15 20 21]
argsort:有返回值,返回的是排序后的索引
arr21.argsort()
array([5, 3, 1, 4, 2, 0], dtype=int64)
arr22=np.array([[12,2,10,9],[2,90,15,1]])
print(arr22)
arr22.sort(axis=1)
print(arr22)
[[12 2 10 9]
[ 2 90 15 1]]
[[ 2 9 10 12]
[ 1 2 15 90]]
arr22=np.array([[12,2,10,9],[2,90,15,1]])
print(arr22)
arr22.sort(axis=0)
print(arr22)
[[12 2 10 9]
[ 2 90 15 1]]
[[ 2 2 10 1]
[12 90 15 9]]
在二维数组里,sort()和argsort()方法都可以写axis参数