图几何交互学习：首次打破几何空间特征嵌入壁垒有何绝招？

点击蓝字

关注我们

AI TIME欢迎每一位AI爱好者的加入！

从图结构数据中学习是机器学习的一个重要任务，图神经网络（GNNs）对此表现出了空前的性能，基于欧氏空间可以很好地解决规则的结构，以及双曲空间可以有效化解层级或无标度结构所带来的挑战。然而现实世界并不总是非黑即白，存在很多融合了各种结构的复杂图。当黑白交织时，如何对图进行有效建模成为了一大难题。

图几何交互学习（GIL）首次打破几何空间特征嵌入的壁垒，将图神经网络拓展到欧氏空间和双曲空间进行交互学习，综合利用双曲和欧几里得拓扑特征的几何表示学习方法，针对不同的几何图派生出一种新颖的距离感知传播和交互学习方案。在AI Time NeurlPS 2020专场四直播间中，我们有幸邀请到了中国科学院大学博士朱时超，为大家分享这项研究工作！

朱时超：本科毕业于哈尔滨工业大学，现为中国科学院大学博士四年级在读学生，导师为王斌，指导老师为周川和潘世瑞，主要研究方向为图神经网络和异质图表示学习的理论研究及其应用。

一、 背景：图交互学习的研究动机

目前GNNs领域大部分工作都是基于欧氏几何空间进行建模的，这是因为向量空间的基本操作都可以欧式空间中使用，具有比较友好和直观的泛化性能。通过欧氏几何建模得到的embedding可以直接用于下游任务，其代表性的工作有GCN、GAT、SAGE等。

但是现实中大多图都表现出非欧氏几何，如层级或无标度结构。对于这类图，如果依然在欧氏空间进行建模的话，可能会造成失真效果。具体来说，就是指我们很难用较低维度的embedding完全覆盖图结构上的信息，造成维度爆炸或失真情况。对此，双曲空间提供了一个比较好的选择。双曲空间中节点和距离是随半径的增长呈指数扩张的，可以很好地建模具有相似增长结构的数据，因此通过较低维度的嵌入就可以覆盖整张图的数据结构，其中代表性的工作有HGCN、HGAT、HGNN等。

现实生活中的图形结构复杂且具有多种属性，如下图所示，蓝色节点相对比较规则，而黄色节点则呈现出树状的层级结构。在一个图中，当可以在欧氏空间轻松捕获的规则结构和在双曲空间更好建模的层级结构都存在时，一个自然的想法是能否用两种空间同时进行建模。这样一来模型就具有了一定的灵活性，不止局限于某一类结构。出于这个动机，朱时超等提出了图几何交互学习，希望可以同时利用欧氏空间和双曲空间的优势来完成图表示学习。

二、先要知识：黎曼流形和图注意力网络

在具体介绍图几何交互学习前，先来简单了解一些先要知识。下图为黎曼流形的定义，介绍它的原因在于欧氏空间和双曲空间都可以归类于黎曼流形。黎曼流形是一组定义了内积的光滑曲面，当中一个很重要的概念是切空间（Tangent space）。切空间是指通过位于曲面上的一点，可以找到一个一阶近似的平面，其属于欧氏空间。通过切空间和黎曼流形曲面可以搭建欧氏空间和双曲空间之间的桥梁，建立联系的具体方式是指数映射。

黎曼流形中另一个重要概念是测地线（Geodesic）。简单来说，把传统欧氏空间中直线的概念迁移到黎曼流形里就叫测地线，即两点之间局部最短的一条曲线。基于测地线可以定义两点之间的距离，而基于距离定义可以产生一个度量空间。当曲面的曲率为零时，就退化成为一个欧氏流形，其距离为传统二范数形式。当曲面的曲率为负数时，就是双曲流形，它也有相应的距离公式以及指数、对数的映射。

图注意力网络（GAT）可解释为在节点上执行注意力消息的传播和更新。下图所列的三个式子是传统GAT的范式，通过赋予邻居信息不同的权重来进行消息的传递和汇聚。

三、图几何交互学习模型

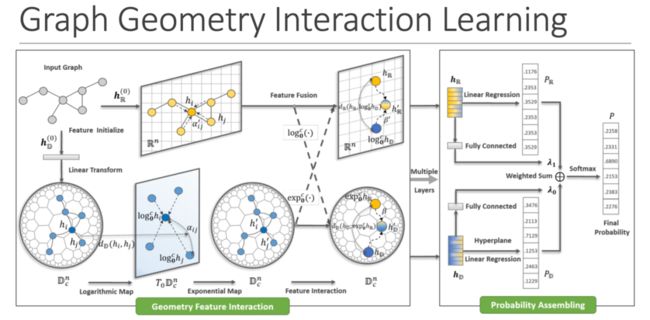
图几何交互学习（GIL）整体模型框架主要分为两个部分，如下图所示，左边是几何特征交互，右边是概率集成。给定一个初始输入图，图本身节点带有初始特征，模型先会对特征进行转换以作为欧氏空间和双曲空间的特征输入。在欧氏空间中，消息的传递和更新主要基于注意力框架。而在双曲空间中，消息的传递和更新是通过对数映射将双曲空间上的操作映射到切空间上完成的。

整个过程为：

（1）在两个空间分别进行embedding学习；

（2）将两个空间学到的特征进行交互和更新，得到各自空间的概率分布，也即下游任务获得的概率；

（3）在概率集成后得到最终任务级别的概率表示。

几何信息传递的具体细节如下图所示，欧氏空间的特征嵌入采用传统的GAT模型。在双曲空间中，首先对输入的特征进行对数映射，通过映射将操作转移到切空间。这样做的原因是双曲空间中的向量加法、乘法等基本操作是不满足交换律和结合律的，为了达到GNNs节点排列不变性的前提要求，需要将节点的聚合操作转换到切空间上进行。

切空间是欧氏空间，上面向量的基本操作都满足交换律和结合律。切空间中同样基于注意力，每个节点的消息汇聚会根据权重进分配，而权重的计算会基于distance-aware attention，换句话说就是学习注意力权值时会考虑在原空间中的距离因素。在切空间完成所有操作以后，再通过指数映射回到原空间。

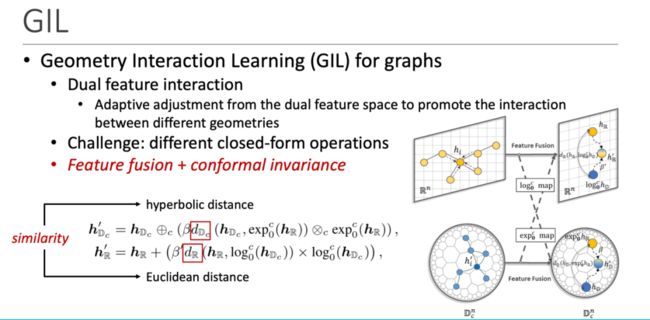
在两个空间各自学到了embedding，接下来需要进行特征交互和融合。因为两个空间基本的向量操作满足不同的闭式操作集，所以需要先将两个空间的特征通过对数或指数映射到对应空间，然后再进行融合。融合操作通过距离度量两个特征的相似度，基于相似度进行特征的校正，以获得融合后的特征。经过两个空间的特征融合，就会获得更新后各自空间的向量表示。

传统欧氏空间softmax是有定义的，而双曲空间并没有，因此需要在双曲空间中定义一个回归。借鉴欧氏空间中softmax的思路，引入仿射超平面作为决策边界，将每一个类别定义为一个超平面，超平面是由法向量和超平面上的一点唯一决定的，而类别的概率是由节点到超平面的距离来度量的。

基于各自空间的softmax回归，可以得到各个空间的概率。模型最终目的是得到某一个点分到某一类别具体的概率值，因此集成操作是必要的。对此，GIL采取的方式是对两个空间概率基于权重进行求和，这里的权重并不是一个超参数，而是通过节点本身在这个空间下特征学到的权重值，即两个空间概率对最终概率的贡献取决于相应空间中的节点特征。这就满足了最开始的一个研究动机，赋予图中每一个节点一个独立的权限，让节点本身确定哪个概率对下游任务更可靠。

四、图几何交互学习实验

为验证GIL的性能，讲者进行了广泛的实验。实验聚焦于Disease、Airport、Cora、Pubmed、Citeseer五个标准数据集，节点分类和链路预测两个任务，下表总结了数据集的统计信息。

在节点分类和链接预测两个任务上的实验结果如下表所示。与基线相比，GIL在这两个任务中的所有五个数据集上均达到了最佳性能，证明了GIL建模同时包含欧氏特征和双曲特征数据集的能力。

为了进一步体现各个模块的效用，还设计了消融实验。首先是不同特征融合对节点分类准确度的影响，结果表明有交互的效用优于没有交互的。另一个是在双曲消息传播中注意力距离对节点分类准确度的影响，结果表明引入注意力性能对任务可以起到较好的提升效果。

为了进一步说明概率集成的影响，在Disease和Citeseer数据集中提取最大连通子图，并绘制其拓扑（见下图），其中节点的颜色表示概率权重，红色代表赋予双曲空间的权重，蓝色代表赋予欧氏空间的权重。可以观察到，在具有分层结构的Disease数据集上，双曲权重总体上大于欧氏权重，而在Citeseer数据集上，两个空间的权重大致相同。另外，边界节点通常具有更多的双曲权重。这与模型的假设一致，即位于较大曲率的节点倾向于更信任双曲嵌入。概率组合在某种程度上为节点表示提供了可解释性。

五、总结

GIL集合了欧氏空间和双曲空间的建模优势，提供了一个更为灵活的框架来建模现实生活中更为复杂的图结构。两个空间整合的特点主要体现在两个方面，一是特征层面的交互，另一个是概率层面的集成。实验结果证明了GIL方法的有效性和可解释性。未来在伪黎曼流形和混合曲率方面，还有很大的空间可以继续深入研究。

参考文献

  e           m     t

往期精彩

 AI                i

整理：何文莉

审稿：朱时超

排版：岳白雪

AI TIME是清华大学计算机系一群关注人工智能发展，并有思想情怀的青年学者们创办的圈子,旨在发扬科学思辨精神，邀请各界人士对人工智能理论、算法、场景、应用的本质问题进行探索，加强思想碰撞，打造一个知识分享的聚集地。

更多资讯请扫码关注

AI TIME欢迎AI领域学者投稿，期待大家剖析学科历史发展和前沿技术。针对热门话题，我们将邀请专家一起论道。同时，我们也长期招募优质的撰稿人，顶级的平台需要顶级的你！

请将简历等信息发至[email protected]！

微信联系:AITIME_HY

 

（直播回放：https://b23.tv/4QPVKJ）

（点击“阅读原文”下载本次报告ppt）