Poisson方程的五点差分格式例题求解
前言
本文将应用偏微分方程数值解中椭圆形方程的五点差分格式求解一道Poisson方程的第一边值例题,通过五点差分格式及边值条件得到相应的差分方程组 K U = F KU=F KU=F后,采用Gauss-seidel迭代法对其求解即可得到数值解,并将数值解与真解作比较.
其中五点差分格式将直接给出,其构造过程从略.
例题
构造Poisson方程第一边值如下:

采用五点差分格式求解并与解析解 u ( x , y ) = x 2 y 2 u(x,y)=x^2y^2 u(x,y)=x2y2进行比较.
( x 和 y x和y x和y方向均 n n n等分,取 h 1 = h 2 = h = 1 / n h_1=h_2=h=1/n h1=h2=h=1/n, x 和 y x和y x和y方向上的节点序号分别用 i , j i,j i,j表示)
符号说明
表1:
| 符号 | 说明 |
|---|---|
| n n n | 区间等分数 |
| h h h | 区间剖分步长 |
| K K K | 方程组系数矩阵 |
| U U U | 方程组未知向量 |
| F F F | 方程组右端项 |
| u u u | 方程组数值解向量 |
| U 1 U_1 U1 | 将 u u u的元素放到矩阵 U 1 U_1 U1中 |
| U 2 U_2 U2 | 解析解矩阵 |
| N N N | 迭代次数上限 |
| e p ep ep | 迭代误差限 |
| k k k | 迭代次数 |
思路
主要思路是将二维问题当成一维问题求解,即二维的 ( n + 1 ) 2 (n+1)^2 (n+1)2个节点按顺序分行放到 ( n + 1 ) 2 (n+1)^2 (n+1)2维向量 U U U中.
主要步骤如下:
1.确定步长后对区域进行网格均匀剖分( x , y x,y x,y方向的步长 h h h相等);
2.所求方程组为 K U = F KU=F KU=F,根据五点差分格式分别给 K K K和 F F F赋值(矩阵中包含边界点);
(说明: U U U是一个 ( n + 1 ) 2 (n+1)^2 (n+1)2维向量,即将求解区域中所有节点放到一个向量 U U U中,当作一维问题进行求解;其次,将边界点放入方程组中可以使 K K K具有更好的性质,更好地防止求解中不收敛的情况,处理边界点时将其当成未知的即可)
3.由边界点值的算术平均值作为 U U U的初始值,以减少迭代次数;
4.给定迭代次数上限 N N N和误差限,由 G a u s s − s e i d e l Gauss-seidel Gauss−seidel迭代求解方程组 K U = F KU=F KU=F得到数值解向量 U U U;
5.为方便观察,将解向量 U U U的元素放入 ( n + 1 ) ∗ ( n + 1 ) (n+1)*(n+1) (n+1)∗(n+1)阶矩阵 U 1 U_1 U1中,并与由解析解 u ( x , y ) = x 2 y 2 u(x,y)=x^2y^2 u(x,y)=x2y2产生的解矩阵 U 2 U_2 U2比较;
求解步骤
划分网格数 n n n选取为7.
1.右端项为 f i j = − 2 [ ( i h ) 2 + ( j h ) 2 ] f_{ij}=-2[(ih)^2+(jh)^2] fij=−2[(ih)2+(jh)2],则得到方程的五点差分格式为
![]()
相应的 G a u s s − s e i d e l Gauss-seidel Gauss−seidel迭代公式为

2.构造求解矩阵时,对特殊类型的节点应根据边界条件将格式适当化简:
(1)左边界点 u 0 j ( j = 0 , 1 , . . . , n ) : 4 u 0 j = 0 u_{0j}(j=0,1,...,n):4u_{0j}=0 u0j(j=0,1,...,n):4u0j=0
(2)下边界点 u i 0 ( i = 0 , 1 , . . . , n ) : 4 u i 0 = 0 u_{i0}(i=0,1,...,n):4u_{i0}=0 ui0(i=0,1,...,n):4ui0=0
(3)右边界点 u n j ( j = 0 , 1 , . . . , n ) : 4 u n j = 4 ( j h ) 2 u_{nj}(j=0,1,...,n):4u_{nj}=4(jh)^2 unj(j=0,1,...,n):4unj=4(jh)2
(4)上边界点 u i n ( i = 0 , 1 , . . . , n ) : 4 u i n = 4 ( i h ) 2 u_{in}(i=0,1,...,n):4u_{in}=4(ih)^2 uin(i=0,1,...,n):4uin=4(ih)2
(5)左边界点的相邻内点 u 1 j ( j = 0 , 1 , . . . , n ) : u_{1j}(j=0,1,...,n): u1j(j=0,1,...,n):
− ( u 2 j − 2 u 1 j ) − ( u 1 , j + 1 − 2 u 1 j + u 1 , j − 1 ) = h 2 f 1 j -(u_{2j}-2u_{1j})-(u_{1,j+1}-2u_{1j}+u_{1,j-1})=h^2f_{1j} −(u2j−2u1j)−(u1,j+1−2u1j+u1,j−1)=h2f1j
(6)下边界点的相邻内点 u i 1 ( i = 0 , 1 , . . . , n ) : u_{i1}(i=0,1,...,n): ui1(i=0,1,...,n):
− ( u i + 1 , 1 − 2 u i 1 + u i − 1 , 1 ) − ( u i 2 − 2 u i 1 ) = h 2 f i 1 -(u_{i+1,1}-2u_{i1}+u_{i-1,1})-(u_{i2}-2u_{i1})=h^2f_{i1} −(ui+1,1−2ui1+ui−1,1)−(ui2−2ui1)=h2fi1
(7)右边界点的相邻内点 u n − 1 , j ( j = 0 , 1 , . . . , n ) : u_{n-1,j}(j=0,1,...,n): un−1,j(j=0,1,...,n):
− ( − 2 u n − 1 , j + u n − 2 , j ) − ( u n − 1 , j + 1 − 2 u n − 1 , j + u n − 1 , j − 1 ) = h 2 f n − 1 , j + ( j h ) 2 -(-2u_{n-1,j}+u_{n-2,j})-(u_{n-1,j+1}-2u_{n-1,j}+u_{n-1,j-1})=h^2f_{n-1,j}+(jh)^2 −(−2un−1,j+un−2,j)−(un−1,j+1−2un−1,j+un−1,j−1)=h2fn−1,j+(jh)2
(8)上边界点的相邻内点 u i , n − 1 ( i = 0 , 1 , . . . , n ) : u_{i,n-1}(i=0,1,...,n): ui,n−1(i=0,1,...,n):
− ( u i + 1 , n − 1 − 2 u i , n − 1 + u i − 1 , n − 1 ) − ( − 2 u i , n − 1 + u i , n − 2 ) = h 2 f i , n − 1 + ( i h ) 2 -(u_{i+1,n-1}-2u_{i,n-1}+u_{i-1,n-1})-(-2u_{i,n-1}+u_{i,n-2})=h^2f_{i,n-1}+(ih)^2 −(ui+1,n−1−2ui,n−1+ui−1,n−1)−(−2ui,n−1+ui,n−2)=h2fi,n−1+(ih)2
对于同时满足上述多个情况的节点,只需根据实际对上述相应格式进行一定的叠加即可.
3.根据五点差分格式和边界条件(步骤2)对 K , U 和 F K,U和F K,U和F赋值(其中选取边界值的算术平均值 Q = 0.3242 Q=0.3242 Q=0.3242为初始近似值赋于未知向量 U U U.)
4.取最大迭代次数N=500,迭代误差限 e p ep ep分别取 1 e − 2 1e-2 1e−2和 1 e − 4 1e-4 1e−4,采用 G a u s s − s e i d e l Gauss-seidel Gauss−seidel迭代求解方程组 K U = F KU=F KU=F,将求解结果放到 ( n + 1 ) 2 (n+1)^2 (n+1)2维向量 u u u中.
5.将最终得到的数值解存储到 ( n + 1 ) (n+1) (n+1)阶矩阵 U 1 U_1 U1中,同时通过理论解 u ( x , y ) = x 2 y 2 u(x,y)=x^2y^2 u(x,y)=x2y2产生相应节点的函数值并存储到 ( n + 1 ) (n+1) (n+1)阶矩阵 U 2 U_2 U2中,将 U 1 , U 2 U_1,U_2 U1,U2的元素进行比较和分析.
求解结果
表2:理论解得到的节点函数值( U 2 中 元 素 U_2中元素 U2中元素)
| u i j u_{ij} uij | i = i= i= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| j = 0 j=0 j=0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0.0004 | 0.0017 | 0.0037 | 0.0067 | 0.0104 | 0.0150 | 0.0204 |
| 2 | 0 | 0.0017 | 0.0067 | 0.0150 | 0.0267 | 0.0416 | 0.0600 | 0.0816 |
| 3 | 0 | 0.0037 | 0.0150 | 0.0337 | 0.0600 | 0.0937 | 0.1349 | 0.1837 |
| 4 | 0 | 0.0067 | 0.0267 | 0.0600 | 0.1066 | 0.1666 | 0.2399 | 0.3265 |
| 5 | 0 | 0.0104 | 0.0416 | 0.0937 | 0.1666 | 0.2603 | 0.3748 | 0.5102 |
| 6 | 0 | 0.0150 | 0.0600 | 0.1349 | 0.2399 | 0.3748 | 0.5398 | 0.7347 |
| 7 | 0 | 0.0204 | 0.0816 | 0.1837 | 0.3265 | 0.5102 | 0.7347 | 1.0000 |
表3: e p = 1 e − 2 ep=1e-2 ep=1e−2时得到的节点函数值( U 1 中 元 素 U_1中元素 U1中元素,此时迭代次数 k = 8 k=8 k=8)
| u i j u_{ij} uij | j = j= j= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| j = 0 j=0 j=0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0.0125 | 0.0203 | 0.0235 | 0.0233 | 0.0219 | 0.0205 | 0.0204 |
| 2 | 0 | 0.0203 | 0.0354 | 0.0454 | 0.0525 | 0.0596 | 0.0687 | 0.0816 |
| 3 | 0 | 0.0235 | 0.0454 | 0.0660 | 0.0877 | 0.1131 | 0.1445 | 0.1837 |
| 4 | 0 | 0.0233 | 0.0525 | 0.0877 | 0.1306 | 0.1835 | 0.2483 | 0.3265 |
| 5 | 0 | 0.0219 | 0.0596 | 0.1131 | 0.1835 | 0.2723 | 0.3808 | 0.5102 |
| 6 | 0 | 0.0205 | 0.0687 | 0.1445 | 0.2483 | 0.3808 | 0.5428 | 0.7347 |
| 7 | 0 | 0.0204 | 0.0816 | 0.1837 | 0.3265 | 0.5102 | 0.7347 | 1.0000 |
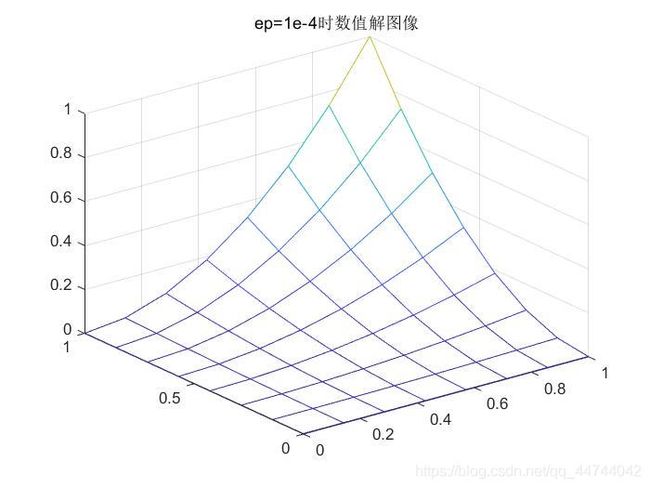
表4: e p = 1 e − 4 ep=1e-4 ep=1e−4时得到的节点函数值( U 1 中 元 素 U_1中元素 U1中元素,此时迭代次数 k = 29 k=29 k=29)
| u i j u_{ij} uij | j = j= j= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| j = 0 j=0 j=0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0.0005 | 0.0019 | 0.0040 | 0.0069 | 0.0105 | 0.0151 | 0.0204 |
| 2 | 0 | 0.0019 | 0.0070 | 0.0153 | 0.0270 | 0.0419 | 0.0601 | 0.0816 |
| 3 | 0 | 0.0040 | 0.0153 | 0.0341 | 0.0603 | 0.0940 | 0.1351 | 0.1837 |
| 4 | 0 | 0.0069 | 0.0270 | 0.0603 | 0.1069 | 0.1668 | 0.2400 | 0.3265 |
| 5 | 0 | 0.0105 | 0.0419 | 0.0940 | 0.1668 | 0.2605 | 0.3749 | 0.5102 |
| 6 | 0 | 0.0151 | 0.0601 | 0.1351 | 0.2400 | 0.3749 | 0.5398 | 0.7347 |
| 7 | 0 | 0.0204 | 0.0816 | 0.1837 | 0.3265 | 0.5102 | 0.7347 | 1.0000 |
通过mesh函数分别将表2-表4的元素可视化,依次得到图1,图2,图3如下.
图1:
总结
通过结果可看出,当迭代误差限不断减小到时,迭代次数从8次上升到29次,方程组数值解也更接近于理论解.本次实验选取大小适中,能够更普遍地反映求解区域中各节点的数值解取值,同时也方便直观地进行比较.可以推断当误差限趋于0时,迭代次数将趋于无穷,此时五点差分格式计算得到的数值解将无限趋近于理论解.但由于选取的误差限较小,节点个数选取仍然较小,我们不易直观地从图1至图3中直观地观察到两次数值结果同理论解之间的差异.
Matlab代码
1.主函数
%% 所求方程为KU=F...
...将二维问题当成一维问题求解,即二维的(n+1)^2个节点按顺序分行放到(n+1)^2维向量U中
clc
n=7; %网格数
h=1/n; %步长
F=zeros((n+1)^2,1); %KU=F
K=zeros(size(F)); %K为(n+1)^2阶方阵
U=ones((n+1)^2,1); %K为(n+1)^2维向量
U0=zeros((n+1)^2,1);%U0用作存边值条件,为初始向量做准备
for i=1:n+1 %对U0中边界点的位置赋值
U0(i)=0; %下边界点
U0(n^2+n+i)=(i*h)^2;%右边界点
U0(1+(i-1)*(n+1))=0;%左边界点
U0(i*(n+1))=(i*h)^2;%上边界点
end
%% 下面对K赋值
for i=1:(n+1)^2
K(i,i)=4;
end
for i=1:n-1 %五点中的右点
for j=2+i*(n+1):(n-1)+i*(n+1)
K(j,j+1)=-1;
end
end
for i=1:n-1 %五点中的左点
for j=3+i*(n+1):n+i*(n+1)
K(j,j-1)=-1;
end
end
for i=1:n-2 %五点中的上点
for j=2+i*(n+1):n+i*(n+1)
K(j,j+n+1)=-1;
end
end
for i=2:n-1 %五点中的下点
for j=2+i*(n+1):n+i*(n+1)
K(j,j-n-1)=-1;
end
end
%% 下面对F赋值
%下面赋值非特殊的点
for i=1:n-1
for j=2+i*(n+1):n+i*(n+1)
F(j)=-2*((floor(j/(n+1)))^2+(mod(j,n+1)-1)^2)*h^4;
end
end
%下面赋值与边界点相邻的内点(左边和下边为齐次,不用管)
for i=1:n-1 %右边的点
F(n+i*(n+1))=F(n+i*(n+1))+(i*h)^2;
end
for i=1:n-1%上边的点
F((n+1)*(n-1)+i+1)=F((n+1)*(n-1)+i+1)+(i*h)^2;
end
%下面赋值F中边界点
for i=i:n+1
F(i)=0;%下边界点
end
for i=1:n-1
F(1+i*(n+1))=0;%左边界点
F((i+1)*(n+1))=4*(i*h)^2;%右边界点
end
for i=(n+1)*n+1:(n+1)^2 %上边界点
if i==(n+1)^2
F(i)=4*(n^2)*(h^2);
else
F(i)=4*((mod(i,n+1)-1)^2)*(h^2);
end
end
%% 下面对U赋初值
d=sum(sum(U0))/4/n; %使用边界点值的算术平均值作为U的初值以加快迭代次数
for i=1:(n+1)^2
U(i)=d;
end
%% 使用高斯赛德迭代求解KU=F
ep=1e-4; %误差限,可根据需要更改,本次我们使用1e-2和1e-4
N=500; %最大迭代次数
u=Gauss(K,F,U,ep,N); %将求解结果存到向量u中
%% 下面将解u放到矩阵U1中,并与真解U2作比较
U1=zeros(n+1);%U1用于存放向量u中元素二维化后的数据
U2=zeros(n+1);%U2用于存放真解
for i=1:n+1%u的一维数据放到二维矩阵U1中
for j=1+(i-1)*(n+1):i*(n+1)
U1(i,j-(i-1)*(n+1))=u(j);
end
end
for i=1:n+1%真解产生的节点函数值放到U2中
for j=1:n+1
U2(i,j)=(((i-1)*h)^2)*(((j-1)*h)^2);
end
end
%% 输出解
U1
U2
%% 画图
X=linspace(0,1,n+1);
Y=linspace(0,1,n+1);
mesh(X,Y,U2);%当要画数值解的图时,U2改为U1即可
hold on;
title('理论解图像');%当要画数值解的图时,'理论解图像'改为'数值解图像'即可
2.Gauss-seidel迭代
function x=Gauss(A,b,x0,ep,N)
%用于Gauss-seidel迭代法解线性方程组Ax=b
%A,b,x0分别为系数矩阵,右端向量和初始向量(初始向量默认为零向量)
%ep为精度(1e-3),N为最大迭代次数(默认500次),x返回数值解向量
n=length(b);
if nargin<5
N=5000;
end
if nargin<4
ep=1e-6;
end
if nargin<3
x0=zeros(n,1);
end
x=zeros(n,1);
k=0;
while k<N
for i=1:n
if i==1
x(1)=(b(1)-A(1,2:n)*x0(2:n))/A(1,1);
elseif i==n
x(n)=(b(n)-A(n,1:n-1)*x(1:n-1))/A(n,n);
else
x(i)=(b(i)-A(i,1:i-1)*x(1:i-1)-A(i,i+1:n)*x0(i+1:n))/A(i,i);
end
end
if norm(x-x0,inf)<ep
break;
end
x0=x;
k=k+1;
end
if k==N
Warning('已到达迭代次数上限');
end
disp(['k=',num2str(k)])
end