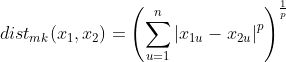【机器学习】——聚类中几种常用的相似度度量
目录
- 距离度量的基本性质
- 八种常用的度量方式
-
- 1、闵可夫斯基距离
- 2、曼哈顿距离
- 3、欧氏距离
- 4、标准欧氏距离
- 5、切比雪夫距离
- 6、马氏距离
- 7、相关系数
- 8、夹角余弦
在 聚类问题中,相似度直接影响聚类的结果,其选择是聚类的根本问题。将样本看作n维向量空间中点的集合,则样本间的相似度可用样本在该向量空间的距离表示。
距离度量的基本性质
-
非负性 :
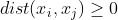
-
同一性:
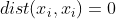
-
对称性:
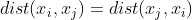
-
直递性:
![]()
可理解为两边之和大于第三边,即三角不等式。
八种常用的度量方式
1、闵可夫斯基距离
定义:给定n维空间中的任意两点
缺点:
(1)没有考虑各个分量量纲不同的问题。
(2)没有考虑各个分量的分布不同的问题
(3)没有考虑变量间的相关关系
因此计算闵可夫斯基距离前常对数据进行标准化和中心化处理 。
2、曼哈顿距离
闵可夫斯基距离是一类距离,当其参数p=1时,称为曼哈顿距离:

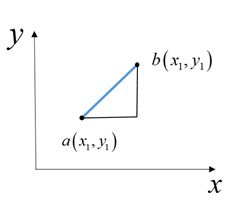
曼哈顿距离又称为计程车距离,其直观表示为两点在n维标准坐标系上的绝对轴距之和。图示为给定二维空间上的两点 ![]()
的曼哈顿距离,不失一般性,可推广到n维空间。
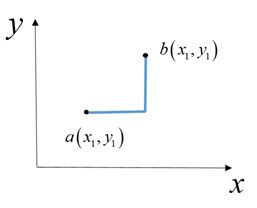
曼哈顿距离计算速度快,某些情况下具有更好的稳定性。但其缺点为如果数据集中某些特征值很大,这些特征会掩盖其他特征间的邻近关系。
Python代码计算曼哈顿距离:
# 计算点a(1,2,3),b(4,5,6)的曼哈顿距离
import numpy as np
def distman(a, b):
return np.sum(abs(a - b))
a=np.array([1,2,3])
b=np.array([4,5,6])
print('a与b的曼哈顿距离:',distman(a,b))
>> a与b的曼哈顿距离: 9
3、欧氏距离
欧几里得距离(欧氏距离)是n维空间中两点的真实距离,直观表示为两点在n维标准坐标系中的直线距离。图示为给定二维空间上的两点
Python代码计算欧几里得距离:
# 计算点a(1,2,3),b(4,5,6)的欧氏距离
import numpy as np
def disted(a, b):
return np.sqrt(np.sum(np.power((a - b), 2)))
a=np.array([1,2,3])
b=np.array([4,5,6])
print('a与b的欧氏距离:',disted(a,b))
>>a与b的欧式距离:5.196152422706632
4、标准欧氏距离
欧几里得距离作为最常用的距离计算方法,具备闵可夫斯基距离共有的一大缺点:将各个分量的量纲,当作相同的看待,这在很多情况下是不符合我们的要求的。标准化欧氏距离便是针对此缺点进行改进的一种距离度量方式。标准欧氏距离先将各个各维空间的分量进行标准化处理,即
# 计算点a(1,2,3),b(4,5,6)的标准欧氏距离
import numpy as np
def distbed(a, b):
X=np.vstack([a,b])
sk=np.var(X,axis=0,ddof=1)
return np.sqrt(np.sum(((a - b) ** 2 /sk)))
a=np.array([1,2,3])
b=np.array([4,5,6])
print('a与b的标准欧式距离:',distbed(a,b))
>> a与b的标准欧式距离: 2.449489742783178
5、切比雪夫距离
当闵可夫斯基距离的参数p=∞时,称为切比雪夫距离:
![]()
切比雪夫距离又称棋盘距离,是n维空间中两点的各坐标值差的绝对值的最大值。其直观表示如图所示,两位置的切比雪夫距离即王从一个位置走到其他位置需要的步数。从图中不难看出,以任一点(边缘点除外)为准,和此点切比雪夫距离为d的点会形成一个各边均与坐标轴平行的边长为2d的正方形。
# 计算点a(1,2,3),b(4,5,6)的切比雪夫距离
import numpy as np
def distcd(a, b):
return max(np.abs(a-b))
a=np.array([1,2,3])
b=np.array([4,5,6])
print('a与b的切比雪夫距离:',distcd(a,b))
>> a与b的切比雪夫距离: 3
6、马氏距离
马氏距离表示协方差距离,它考虑了各个特征之间的相关性和量纲问题 ,使用马氏距离可有效排除变量间相关性的干扰且不受原始数据测量单位影响,因此是一种较为常用的相似度度量方式。给定n维空间中的一个样本集合X,其协方差矩阵为S,样本集合中任意两点 ![]()
之间的马氏距离为:
![]()
观察上述公式,在S为单位矩阵时(各个维度相互独立且方差为1),马氏距离即为欧氏距离,因此欧氏距离是马氏距离的特殊形式。
从公式可以看到,在马氏距离计算公式中用到了协方差矩阵的逆矩阵,这就要求使用马氏距离时样本数据量大于特征维数,否则逆矩阵不存在。另一种情况是样本在所处的空间平面内共线,此时逆矩阵也不存在。在这两种情况下,采用欧氏距离度量。而在实际应用中,样本数据量大于特征维数很容易满足,而样本在空间平面共线也是很少发生的,因此马氏距离在绝大多数情况下是适用的。
Python代码计算马氏距离:
# 计算点a(1,8,3),b(4,1,6)的马氏距离
import numpy as np
def distmd(a, b):
X=np.vstack([a, b])
XT=X.T
S=np.cov(X)
n=XT.shape[0]
for i in range(0,n):
for j in range(i+1,n):
d=np.sqrt(np.dot(np.dot(XT[i]-XT[j],np.linalg.inv(S)),(XT[i]-XT[j]).T))
return d
a=np.array([1,8,3])
b=np.array([4,1,6])
print('a与b的马氏距离:',distmd(a,b))
>>a与b的马氏距离:1.9999999999999998
7、相关系数
相关系数是一个衡量两个样本间相似度的指标,表示线性相关程度的大小,其取值范围为[-1,1],相关系数的绝对值越接近1则样本越相似,越接近于0越不相似。给定n维空间中的任意两点 ,这两点间的相关系数为:
# 计算点a(1,2,3),b(4,5,6)的相关系数
import numpy as np
def r(a,b):
cov = np.sum(((a - a.mean()) * (b - b.mean())))
var = np.sqrt(np.sum((a - a.mean()) ** 2)) * np.sqrt(np.sum((b - b.mean()) ** 2))
return cov/var
a= np.array([ 1, 2, 3])
b= np.array([ 4, 5, 6])
print('a与b的相关系数:', r(x, y))
>>a与b的相关系数: 0.9999999999999998
8、夹角余弦
夹角余弦是用n维空间中两个向量的夹角的余弦值衡量两样本间差异大小,其取值范围为[-1,1],夹角越接近1则夹角越小,两样本相似度越高。图示为给定二维空间上的两向量 ![]()
的夹角余弦, 不失一般性,可推广到n维空间。
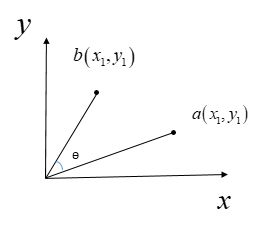
给定n维空间中的任意两向量
# 计算点a(1,2,3),b(4,5,6)的夹角余弦
import numpy as np
def cos(a,b):
m=np.sum(a*b.T)
n=np.sqrt(np.sum(a*a.T))*np.sqrt(np.sum(b*b.T))
return (m/n)
a=np.array([1,2,3])
b=np.array([4,5,6])
print('a与b的夹角余弦:', cos(a,b))
>>a与b的夹角余弦: 0.9746318461970762
在聚类中,使用不同方式度量相似度可能会得到不同结果,因此在进行聚类时,选择适当的距离或相似度非常重要。