智能优化算法:灰狼优化算法-附代码
智能优化算法:灰狼优化算法-附代码
文章目录
- 智能优化算法:灰狼优化算法-附代码
-
- 1.算法原理
-
- 1.1 包围猎物
- 1.2 狩猎
- 1.3 攻击猎物(开发)
- 1.4 搜索猎物(勘探)
- 2.算法流程图
- 3.算法结果
- 4.参考文献
- 5.Matlab 代码
- 6.Python代码
摘要:受 灰 狼 群 体 捕 食 行 为 的 启 发,Mirjalili等[1]于 2014年提出了一种新型群体智能优化算法:灰狼优化算法。GWO通过模拟灰狼群体捕食行为,基于狼群群体协作的机制来达到优化的目的。 GWO算法具有结构简单、需要调节的参数少,容易实现等特点,其中存在能够自适应调整的收敛因子以及信息反馈机制,能够在局部寻优与全局搜索之间实现平衡,因此在对问题的求解精度和收敛速度方面都有良好的性能。
1.算法原理
灰狼属于犬科动物,被认为是顶级的掠食者,它们处于生物圈食物链的顶端。灰狼大多喜欢群居,每个群体中平均有5-12只狼。特别令人感兴趣的是,它们具有非常严格的社会等级层次制度,如图1所示。金字塔第一层为种群中的领导者,称为 α 。在狼群中 α 是具有管理能力的个体,主要负责关于狩猎、睡觉的时间和地方、食物分配等群体中各项决策的事务。金字塔第二层是 α 的智囊团队,称为 β 。 β 主要负责协助α 进行决策。当整个狼群的 α 出现空缺时,β 将接替 α 的位置。 β 在狼群中的支配权仅次于 α,它将 α 的命令下达给其他成员,并将其他成员的执行情况反馈给 α 起着桥梁的作用。金字塔第三层是 δ ,δ 听从 α 和 β 的决策命令,主要负责侦查、放哨、看护等事务。适应度不好的 α 和 β 也会降为 δ 。金字塔最底层是 ω ,主要负责种群内部关系的平衡。
此外,集体狩猎是灰狼的另一个迷人的社会行为。灰狼的社会等级在群体狩猎过程中发挥着重要的作用,捕食的过程在 α 的带领下完成。灰狼的狩猎包括以下 3个主要部分:
1)跟踪、追逐和接近猎物;
2)追捕、包围和骚扰猎物,直到它停止移动;
3)攻击猎物
1.1 包围猎物
在狩猎过程中,将灰狼围捕猎物的行为定义如下:
D ⃗ = ∣ C ⃗ . X p ⃗ ( t ) − X ⃗ ( t ) (1) \vec{D}=|\vec{C}.\vec{X_{p}}(t)-\vec{X}(t) \tag{1} D=∣C.Xp(t)−X(t)(1)
X ⃗ ( t + 1 ) = X p ⃗ ( t ) − A ⃗ . D ⃗ (2) \vec{X}(t+1)=\vec{X_{p}}(t)-\vec{A}.\vec{D}\tag{2} X(t+1)=Xp(t)−A.D(2)
式(1)表示个体与猎物间的距离,式(2)是灰狼的位置更新公式。其中, t t t 是目前的迭代代数, A ⃗ \vec{A} A和 C ⃗ \vec{C} C是系数向量, X p ⃗ \vec{X_{p}} Xp和 X ⃗ \vec{X} X分别是猎物的位置向量和灰狼的位置向量。 A ⃗ \vec{A} A和 C ⃗ \vec{C} C的计算公式如下:
A ⃗ = 2 a ⃗ . r 1 ⃗ − a ⃗ (3) \vec{A} = 2\vec{a}.\vec{r_{1}}-\vec{a}\tag{3} A=2a.r1−a(3)
C ⃗ = 2. r 2 ⃗ (4) \vec{C}=2.\vec{r_{2}}\tag{4} C=2.r2(4)
其中, a ⃗ \vec{a} a是收敛因子,随着迭代次数从2线性减小到0, r 1 ⃗ \vec{r_{1}} r1和 r 2 ⃗ \vec{r_{2}} r2的模取[0,1]之间的随机数。
1.2 狩猎
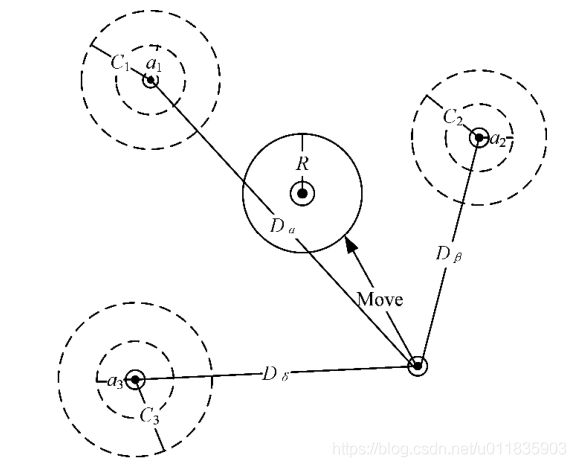
灰狼能够识别猎物的位置并包围它们。当灰狼识别出猎物的位置后,β 和 δ 在 α 的带领下指导狼群包围猎物。在优化问题的决策空间中,我们对最佳解决方案(猎物的位置)并不了解。因此,为了模拟灰狼的狩猎行为,我们假设 α ,β 和 δ 更了解猎物的潜在位置。我们保存迄今为止取得的3个最优解决方案,并利用这三者的位置来判断猎物所在的位置,同时强迫其他灰狼个体(包括 ω )依据最优灰狼个体的位置来更新其位置,逐渐逼近猎物。狼群内个体跟踪猎物位置的机制如图2所示。
灰狼个体跟踪猎物位置的数学模型描述如下:
{ D α ⃗ = ∣ C 1 ⃗ . X α ⃗ − X ⃗ ∣ D β ⃗ = ∣ C 2 ⃗ . X β ⃗ − X ⃗ ∣ D δ ⃗ = ∣ C 1 ⃗ . X δ ⃗ − X ⃗ ∣ (5) \begin{cases}\vec{D_{\alpha}}=|\vec{C_{1}}.\vec{X_{\alpha}}-\vec{X}|\\ \vec{D_{\beta}} = |\vec{C_{2}}.\vec{X_{\beta}}-\vec{X}|\\ \vec{D_{\delta}}=|\vec{C_{1}}.\vec{X_{\delta}}-\vec{X}|\end{cases}\tag{5} ⎩⎪⎨⎪⎧Dα=∣C1.Xα−X∣Dβ=∣C2.Xβ−X∣Dδ=∣C1.Xδ−X∣(5)
其中, D α ⃗ , D β ⃗ , D δ ⃗ \vec{D_{\alpha}},\vec{D_{\beta}},\vec{D_{\delta}} Dα,Dβ,Dδ分别表示分别表示 α , β 和 δ 与其他个体间的距离。 X α ⃗ , X β ⃗ , X δ ⃗ \vec{X_{\alpha}},\vec{X_{\beta}},\vec{X_{\delta}} Xα,Xβ,Xδ分别代表 α , β 和 δ 的当前位置; C 1 ⃗ , C 2 ⃗ , C 3 ⃗ \vec{C_{1}},\vec{C_{2}},\vec{C_{3}} C1,C2,C3是随机向量, X ⃗ \vec{X} X是当前灰狼的位置。
{ X 1 ⃗ = X a ⃗ − A 1 . D α ⃗ X 2 ⃗ = X β ⃗ − A 2 . D β ⃗ X 3 ⃗ = X δ ⃗ − A 3 . D δ ⃗ (6) \begin{cases}\vec{X_{1}}=\vec{X_{a}}-A_{1}.\vec{D_{\alpha}}\\ \vec{X_{2}}=\vec{X_{\beta}}-A_{2}.\vec{D_{\beta}}\\\vec{X_{3}}=\vec{X_{\delta}}-A_{3}.\vec{D_{\delta}} \end{cases}\tag{6} ⎩⎪⎨⎪⎧X1=Xa−A1.DαX2=Xβ−A2.DβX3=Xδ−A3.Dδ(6)
X ⃗ ( t + 1 ) = X 1 ⃗ + X 2 ⃗ + X 3 ⃗ 3 (7) \vec{X}(t+1)=\frac {\vec{X_{1}}+\vec{X_{2}}+\vec{X_{3}}}{3}\tag{7} X(t+1)=3X1+X2+X3(7)
式(6)分别定义了狼群中 ω 个体朝向 α ,β 和 δ 前进的步长和方向,式(7)定义了 ω 的最终位置。
1.3 攻击猎物(开发)
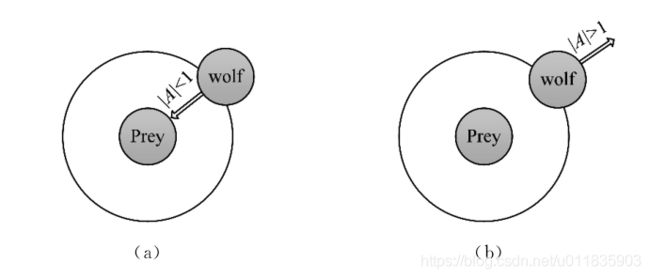
当猎物停止移动时,灰狼通过攻击来完成狩猎过程。为了模拟逼近猎物, a ⃗ \vec{a} a 的值被逐渐减小,因此 A ⃗ \vec{A} A的波动范围也随之减小。换句话说,在迭代过程中,当 a ⃗ \vec{a} a的值从2线性下降到0时,其对应的 A ⃗ \vec{A} A的值也在区间[-a,a]内变化。如图3a所示,当 A ⃗ \vec{A} A的值位于区间内时,灰狼的下一位置可以位于其当前位置和猎物位置之间的任意位置。当 ∣ A ⃗ ∣ < 1 |\vec{A}|<1 ∣A∣<1 时,狼群向猎物发起攻击(陷入局部最优)。
1.4 搜索猎物(勘探)
灰狼根据 α ,β 和 δ 的位置来搜索猎物。灰狼在寻找猎物时彼此分开,然后聚集在一起攻击猎物。基于数学建模的散度,可以用 A ⃗ \vec{A} A大于1 或小于-1 的随机值来迫使灰狼与猎物分离,这强调了勘探(探索)并允许 GWO 算法全局搜索最优解。如图3b所示, ∣ A ⃗ ∣ > 1 |\vec{A}|>1 ∣A∣>1 强迫灰狼与猎物(局部最优)分离,希望找到更合适的猎物(全局最优)。GWO 算法还有另一个组件 C ⃗ \vec{C} C来帮助发现新的解决方案。由式(4)可知, C ⃗ \vec{C} C是[0,2]之间的随机值。 C C C 表示狼所在的位置对猎物影响的随机权重, C > 1 C>1 C>1表示影响权重大,反之,表示影响权重小。这有助于 GWO算法更随机地表现并支持探索,同时可在优化过程中避免陷入局部最优。另外,与 A A A不同 C C C是非线性减小的。这样,从最初的迭代到最终的迭代中,它都提供了决策空间中的全局搜索。在算法陷入了局部最优并且不易跳出时, C C C的随机性在避免局部最优方面发挥了非常重要的作用,尤其是在最后需要获得全局最优解的迭代中。
2.算法流程图
3.算法结果
4.参考文献
[1] Seyedali Mirjalili,Seyed Mohammad Mirjalili,Andrew Lewis. Grey Wolf Optimizer[J]. Advances in Engineering Software,2014,69.
[2] 张晓凤,王秀英.灰狼优化算法研究综述[J].计算机科学,2019,46(03):30-38.
5.Matlab 代码
https://mianbaoduo.com/o/bread/Z5ecmZc=
6.Python代码
https://mianbaoduo.com/o/bread/aZ2Wl54=