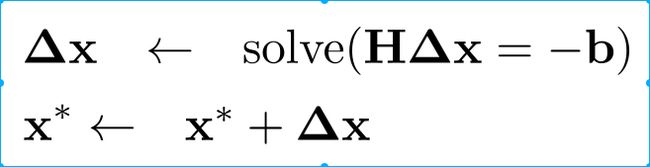g2o原理及应用（一）

g2o是一个通用的图优化框架。
本文结合论文g2o: A general framework fo graph optimizaiton说明g2o的理论，然后编写一个示例程序，说明g2o的使用方法。

g2o理论：
许多问题可以建模为最小二乘优化的状态估计问题。问题形式如图

F(x)为目标函数，目的就是求解状态x，使目标函数最小。x是一个向量，向量中的每个元素也可以为一个参数块。zij是联系状态变量i和状态变量j的观测，数学上表现为一个约束方程。由于有测量噪声，采用误差向量e()评价xi和xj满足方程的程度。

论文中为了简化符号，采用下图描述误差向量

这里需要注意的是，状态变量xi和xj（左侧），已经变为了整个系统的状态x（右侧）。

这个误差向量可以表示为一个有向图，可以知道方程结构，便于可视化分析

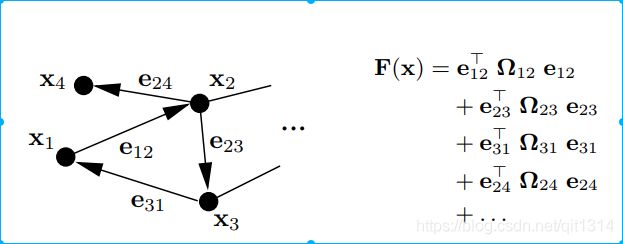
这个图中，边的个数就是所有的约束，也就是方程个数。一个节点为一个状态变量，所有节点的结合组成了整个系统的状态变量。不要忘记我们的目标就是为了状态估计。

有了上述目标函数，我们就可以进行最小二乘优化。
论文中给出的是高斯牛顿法。
高斯牛顿法的思想是：对误差函数e采用一阶泰勒展开。然后构建一个新的误差函数，求这个误差函数的极小值，以极小值作为新的迭代点。重复迭代，直到满足终止条件。

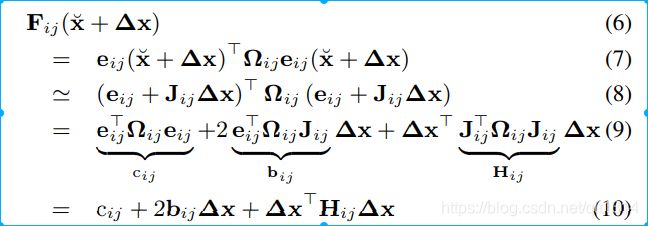
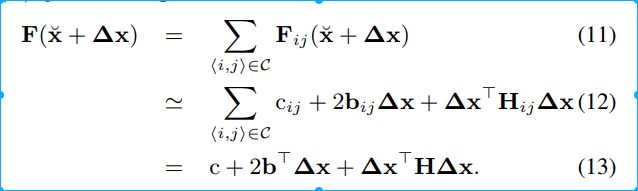
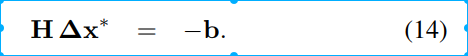
这里需要注意的是，我们要求的是\delta x,
雅克比矩阵Jij为zij的方程对整个状态变量x的雅克比,
方程14的H和b有关的参数为Jij.

也就是说，我们通过求解整个方程的雅克比，然后带入到方程12中，组合为b和H，最后求解H\delta x = -b.

论文中还粗略介绍了LM方法，

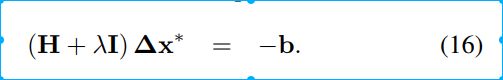
在线性方程中加入了一个带有阻尼系数的单位阵。
这里不详细介绍了。

最小二乘在SLAM中的应用
空间刚体有6个自由度，三个旋转，3个平移。
平移位于欧式空间，但是旋转位于非欧空间。

表示旋转的方法有旋转矩阵、欧拉角、四元数、旋转向量。
欧拉角和旋转向量是最小参数表示，但是有奇异性。
旋转矩阵和四元数是过参数表示（3个自由度，但是旋转矩阵9个参数，四元数4个参数），但是会有约束。

为了应用最小二乘，可以把\delta x最小参数表示，因为通常\delta x 比较小，远离奇异点。
然后采用过参数表示当前的迭代点。
定义了一个田字格操作。

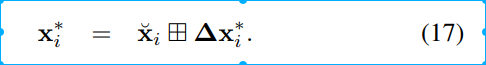
论文中说，可以采用归一化的四元数表示增量，采用全四元数表示迭代点，这里当前还没弄明白。

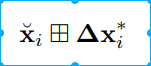
田字格和准星是有关系的，这里也就是两个旋转矩阵相乘，可以表示相机从当前位姿，运动\delta x，后的新的位姿

新的误差函数形式如图

重要的雅克比如图，这玩意就和求导一样的

新的迭代点为

不管参数咋样变化，H矩阵的结构是不变的。

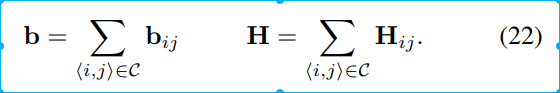
也就是说，每个方程都会有一个bij和一个Hij，所有方程的H和b组成了系统的H和b。

注意：bij与三个东西有关。
假设有n个变量，每个变量是个参数块，假设只有1个参数，则Jij为1Xn的，\Omiga为1X1的，e为1X1，则bij为nx1的向量。

同理Hij = nX1X1X1X1Xn = nXn 的矩阵。

也就是在H的ij，ji，ii，jj和b的i和j位置非零，其他位置为0.

可以注意到H也是图的邻接矩阵，所以，H的非零块正比于图中边的数量。这导致了H的稀疏性。
有些问题可以采用H的系数性，来求解线性系统。

在BA中，变量为相机姿态p和路标点l
重新排列变量顺序，

由于通常相机变量个数少，路标点变量个数多，
采用H的舒尔补，可以化简。

Hll的逆是块对角阵，便于求解。并且方程个数少了，可以求解\delta x_p
然后可求\delta x_l

实现方法：

小结：

对每个观测，计算误差向量；
计算误差向量的雅克比；
更新系统的H和b

然后求解线性系统

应用：
在使用g2o时，我们需要以图优化的思想来编写程序。

图是由节点和边组成的，我们首先以类的形式，定义节点和边。

顶点可以继承一个模板类BaseVertex，模板参数为顶点的最小参数个数和顶点的数据类型。
需要我们实现的是田操作，重写 virtual void oplusImpl(const double* update) 函数。
估计值存储在变量_estimate中；函数void setToOriginImpl() 将节点的值进行重置。定义节点时，利用setEstimate(type) 函数来设定初始值；setId(int) 定义节点编号。

边也是继承一个模板类，模板参数为误差向量e的维度，观测z的数据类型和边连接的顶点类型。这里需要注意的是，几个顶点就是几元边。
边也就是上文中的eij，我们需要为边定义误差函数void computeError()
定义雅克比Jij void linearizeOplus() ,观测值存储在_measurement 中，误差存储在_error 中，节点存储在_vertices[] 。定义边时，利用setId(int) 来定义边的编号（决定了在H矩阵中的位置）；setMeasurement(type) 函数来定义观测值；setVertex(int, vertex) 来定义节点；setInformation() 来定义协方差矩阵的逆。

定义完顶点和边后，我们就可以构建这个图，并对其优化。

定义一个图优化的对象 g2o::SparseOptimizer optimizer;
设置一些图优化相关的内容，
也就是有了线性系统H\deltax=-b后，我们还需要设定求解线性系统的方法。
线性系统可以是带阻尼的LM方法，这就需要我们指定用哪个优化算法
g2o::OptimizationAlgorithmLevenberg

  typedef g2o::BlockSolver< g2o::BlockSolverTraits >  MyBlockSolver;
  typedef g2o::LinearSolverDense MyLinearSolver;
  
  MyLinearSolver* linearSolver = new MyLinearSolver();//定义一个线性求解器
  MyBlockSolver* solver_ptr = new MyBlockSolver(linearSolver);//定义一个块求解器
  g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg(solver_ptr);//定义优化方法
  optimizer.setAlgorithm(solver);//设置图优化的求解器

这里是自下而上的设置。
块求解器这块还没看懂，

之后添加顶点和边。

最后优化

 optimizer.initializeOptimization();
  optimizer.setVerbose(verbose);
  optimizer.optimize(maxIterations);