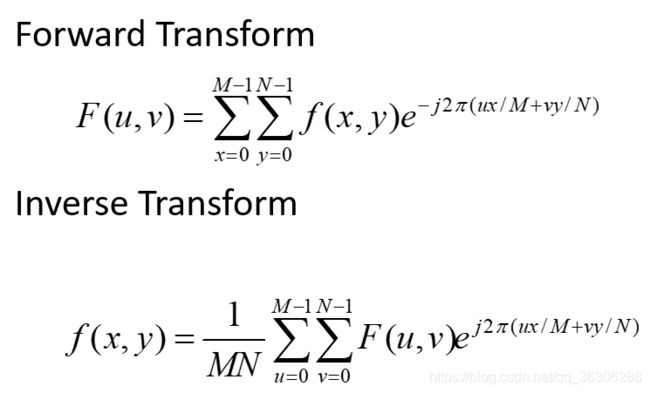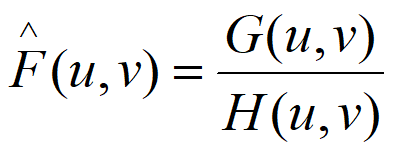DIP2020复习总结(六)
DIP复习总结
- Part8 频域滤波 filtering in the frequency domain
-
- 2D DFT IDFT
-
- 基本思想
- 加速算法
- FFT shift
- 同态滤波 Homomorphic Filtering
- Bandreject & Bandpass 带阻和带通滤波
-
- 图示
- 带阻 带通应用和原理
- 陷波滤波器 Notch reject or pass
-
- 原理
- Part9 图像恢复 image restoration
-
- 降级模型
-
- 逆滤波
- 主要参考
Part8 频域滤波 filtering in the frequency domain
主要内容包括一些点、线、边缘的检测算子和检测原理。
2D DFT IDFT
基本思想
前向传播和反向传播
Complex DFT(Complex[,]f,int u,int v)
{
int M = f.GetLength(0);
int N = f.GetLength(1);
Complex Fuv = new Complex(0,0);
for (int x=0;x<M;x++)
for (int y=0;y<N;y++)
{
double a = -2*Math.PI*((double)u*x/M+(double)v*y/N);
Fuv += f[x,y]*new Complex(Cos(a),Sin(a));
}
return Fuv;
}
Complex[,] DFT(Complex[,] f)
{
int M = f.GetLength(0);
int N = f.GetLength(1);
Complex[,] F = new Complex[M, N];
double Pi = 3.1415926;
for (int u = 0; u < M; u++)
for (int v = 0; v < N; v++)
{
F[u, v] = new Complex(0, 0);
for (int x = 0; x < M; x++)
for (int y = 0; y < N; y++)
{
double a = 2*Pi * ((double)u * x / M + (double)v * y / N);
F[u, v] += f[x, y] * new Complex(Math.Cos(-a), Math.Sin(-a));
}
}
return F;
}
Complex[,] IDFT(Complex[,] F)
{
int M = F.GetLength(0);
int N = F.GetLength(1);
Complex[,] f = new Complex[M, N];
double Pi = 3.1415926;
for (int x = 0; x < M; x++)
for (int y = 0; y < N; y++)
{
f[x, y] = new Complex(0, 0);
for (int u = 0; u < M; u++)
for (int v = 0; v < N; v++)
{
double a = 2*Pi *((double)u * x / M + (double)v * y / N);
f[x, y] += F[u, v] * new Complex(Math.Cos(a), Math.Sin(a));
}
f[x, y] *= 1.0 / (M * N);
}
return f;
}
byte[,] ToByte(Complex[,] f)
{
int w = f.GetLength(0);
int h = f.GetLength(1);
byte[,] g = new byte[w, h];
for (int y = 0; y < h; y++)
for (int x = 0; x < w; x++)
{
g[x, y] = SByte(f[x, y].Real);
}
return g;
}
Complex[,] ToComplex(byte[,] f)
{
int w = f.GetLength(0);
int h = f.GetLength(1);
Complex[,] g = new Complex[w, h];
for (int y = 0; y < h; y++)
for (int x = 0; x < w; x++)
{
g[x, y] = new Complex(f[x, y], 0);
}
return g;
}
byte SByte(double v)
{
if (v > 255) return 255;
if (v < 0) return 0;
return (byte)v;
}
void main()
{
byte[,] f = LoadImg();
ShowImg("f",f);
DateTime t0 = DateTime.Now;
Complex[,] F = DFT(ToComplex(f));
byte[,] f_ = ToByte(IDFT(F));
DateTime t1 = DateTime.Now;
print((t1-t0));
ShowImg("f_",f_);
}
加速算法
void DFT(Complex[] f, Complex[] F) // 1D DFT
{
int N = f.GetLength(0);
double Pi = 3.1415926;
for (int u = 0; u < N; u++)
{
F[u] = new Complex(0, 0);
for (int n = 0; n < N; n++)
{
double a = 2*Pi*((double)u * n / N);
F[u] += f[n] * new Complex(Math.Cos(-a), Math.Sin(-a));
}
}
}
Complex[,] DFT_V(Complex[,] f) //求垂直方向的1D DFT
{
int M = f.GetLength(0);
int N = f.GetLength(1);
Complex[,] F = new Complex[M, N];
Complex[] f_ = new Complex[N];
Complex[] F_ = new Complex[N];
for (int x=0;x<M;x++)
{
for (int y=0;y<N;y++)
f_[y] = f[x,y];
DFT(f_,F_);
for (int y=0;y<N;y++)
F[x,y] = F_[y];
}
return F;
}
Complex[,] DFT_H(Complex[,] f) //求水平方向的1D DFT
{
int M = f.GetLength(0);
int N = f.GetLength(1);
Complex[,] F = new Complex[M, N];
Complex[] f_ = new Complex[M];
Complex[] F_ = new Complex[M];
for (int y=0;y<N;y++)
{
for (int x=0;x<M;x++)
f_[x] = f[x,y];
DFT(f_,F_);
for (int x=0;x<M;x++)
F[x,y] = F_[x];
}
return F;
}
Complex[,] DFT(Complex[,] f) // 结合起来
{
return DFT_H(DFT_V(f));
}
Complex[,] IDFT(Complex[,] F)
{
int M = F.GetLength(0);
int N = F.GetLength(1);
Complex[,] f = new Complex[M, N];
double Pi = 3.1415926;
for (int x = 0; x < M; x++)
for (int y = 0; y < N; y++)
{
f[x, y] = new Complex(0, 0);
for (int u = 0; u < M; u++)
for (int v = 0; v < N; v++)
{
double a = 2*Pi *((double)u * x / M + (double)v * y / N);
f[x, y] += F[u, v] * new Complex(Math.Cos(a), Math.Sin(a));
}
f[x, y] *= 1.0 / (M * N);
}
return f;
}
byte[,] ToByte(Complex[,] f)
{
int w = f.GetLength(0);
int h = f.GetLength(1);
byte[,] g = new byte[w, h];
for (int y = 0; y < h; y++)
for (int x = 0; x < w; x++)
{
g[x, y] = SByte(f[x, y].Real);
}
return g;
}
Complex[,] ToComplex(byte[,] f)
{
int w = f.GetLength(0);
int h = f.GetLength(1);
Complex[,] g = new Complex[w, h];
for (int y = 0; y < h; y++)
for (int x = 0; x < w; x++)
{
g[x, y] = new Complex(f[x, y], 0);
}
return g;
}
byte SByte(double v)
{
if (v > 255) return 255;
if (v < 0) return 0;
return (byte)v;
}
void main()
{
byte[,] f = LoadImg();
ShowImg("f",f);
DateTime t0 = DateTime.Now;
Complex[,] F = DFT(ToComplex(f));
byte[,] f_ = ToByte(IDFT(F));
DateTime t1 = DateTime.Now;
print((t1-t0));
ShowImg("f_",f_);
}
FFT shift
同态滤波 Homomorphic Filtering
基本原理:对于图像而言,可以表示为照射和反射两个分量,如下:

然后按照下面的流程对图片进行处理即可;H是滤波器
Bandreject & Bandpass 带阻和带通滤波
图示
带阻 带通应用和原理
其表达式如下:
byte[,] GBandReject(int w,int h,double D0,double w0)
{
byte[,] g = new byte[w,h];
for (int y=0;y<h;y++)
for (int x=0;x<w;x++)
{
double D = Sqrt((x-w/2)*(x-w/2)+(y-h/2)*(y-h/2));
g[x,y] = (byte)(255-255*Exp(-(D-D0)*(D-D0)/(2*w0*w0)));
}
return g;
}
byte[,] GBandPass(int w,int h,double D0,double w0)
{
byte[,] g = new byte[w,h];
for (int y=0;y<h;y++)
for (int x=0;x<w;x++)
{
double D = Sqrt((x-w/2)*(x-w/2)+(y-h/2)*(y-h/2));
g[x,y] = (byte)(255*Exp(-(D-D0)*(D-D0)/(2*w0*w0)));
}
return g;
}
陷波滤波器 Notch reject or pass
原理
每个陷波对都是成对出现,其中心为(uk,vk)(-uk,-vk)(根据图像中心M/2,N/2来决定)



带通的话,用1-带阻即可
Part9 图像恢复 image restoration
降级模型


同之前一样,可以使用如下的操作,来对图像进行滤波

频域的话是这两个???