tensorflow2.0实现DeepFM

本文基于tensorflow2.0实现的DeepFM 结构。数据集： Criteo 的500000条数据子集。

必要的库

import pandas as pd
import numpy as np
import tensorflow as tf
from tensorflow.keras.layers import *
from sklearn.preprocessing import LabelEncoder
import tensorflow.keras.backend as K 
from tensorflow.keras.models import Model

数据预处理

Criteo 数据集一共39个特征，1个label特征，如下图所示：以 l 开头的是数值型特征，以 C 开头的是类别型特征。

train = pd.read_csv('./criteo_sampled_data.csv')
train.head()

首先，我们对数据进行简单的处理。

定义特征组

dense_feats = [f for f in cols if f[0] == 'I']
sparse_feats = [f for f in cols if f[0] == 'C']

对于数值型特征，用 0 填充，然后进行log变换。

def process_dense_feats(data,feats):
    d  = data.copy()
    d = d[feats].fillna(0.0)
    for f in feats:
        d[f] = d[f].apply(lambda x: np.log(x+1) if x>-1 else -1)
    return d
data_dense = process_dense_feats(train, dense_feats)

对于类别型特征，用’-1’填充，然后进行类别编码。

def process_spares_feats(data,feats):
    d = data.copy()
    d = d[feats].fillna('-1')
    for f in feats:
        d[f] = LabelEncoder().fit_transform(d[f])
    return d
data_sparse = process_spares_feats(train,sparse_feats)

合并处理后的特征，加入label

total_data = pd.concat([data_dense,data_sparse],axis=1)
total_data['label'] = train['label']

模型的构建与训练

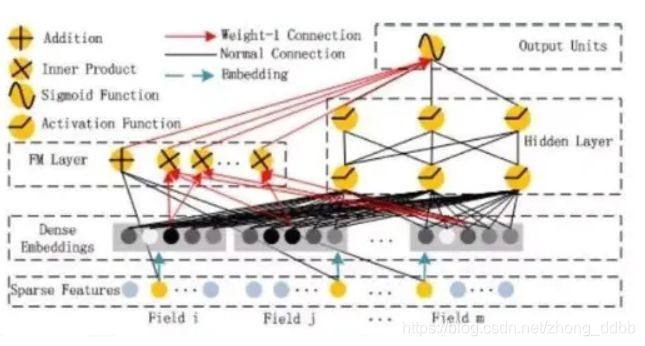
DeepFM的模型结构如下：

神经网络部分与因子分解机部分，分别负责低阶特征的提取和高阶特征的提取。这两部分共享同样的输入。具体的理论可以参考：FM系列—DeepFFM、DeepFM 结构详解

FM部分

主要数学原理如下：
$$\begin{gathered} y_{FM}=w_0+\sum _{i=1}^n{w}_i{x}_i+\sum _i^n\sum _{j=i+1}^n<v_i,v_j>x_i{x}_j \\ <v_i,v_j>=\sum _{f=1}^k{v}_{if}{v}_{jf} \end{gathered}$$

一阶特征

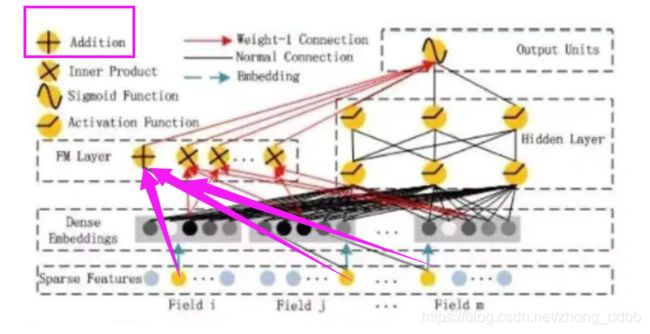
一阶特征类似于逻辑回归，如下图的紫色部分：

对于每一个sparse Features 特征，在FM的原理中，一般都是进行one-hot后在进行交叉特征，但是由于稀疏的存在，很多位置的$x_i=0$，对应的$w_i{x}_i=0$。因此，可以将sparse 特征embedding到1维，对应的值也就是$w_i{x}_i$的值。

举例说明：假设某品牌有三种取值，进行one-hot后，得到商品为[0,0,1]，我们进行线性回归时会得到$w_1\times 0+w_2\times 0+w_3\times 1$ ，只有$w_3$被保留。所以，可以对商品构造一个3*1的embedding向量，向量的值就是对应的系数。

对sparse_feat 具体代码如下：

# 单独对每一个 sparse 特征构造输入
sparse_inputs = []
for f in sparse_feats:
    _input = Input([1], name=f)
    sparse_inputs.append(_input)
    
sparse_1d_embed = []
for i, _input in enumerate(sparse_inputs):
    f = sparse_feats[i]
    voc_size = total_data[f].nunique()
    # 使用 l2 正则化防止过拟合
    reg = tf.keras.regularizers.l2(0.5)
    _embed = Embedding(voc_size, 1, embeddings_regularizer=reg)(_input)
    # 由于 Embedding 的结果是二维的，
    # 因此如果需要在 Embedding 之后加入 Dense 层，则需要先连接上 Flatten 层
    _embed = Flatten()(_embed)
    sparse_1d_embed.append(_embed)
# 对每个 embedding lookup 的结果 wi 求和
fst_order_sparse_layer = Add()(sparse_1d_embed)

图中只有sparse_feat的一阶特征。我们额外加入dense_feat的一阶特征。

# 构造每个 dense 特征的输入
dense_inputs = []
for f in dense_feats:
    _input = Input([1], name=f)
    dense_inputs.append(_input)
# 将输入拼接到一起，方便连接 Dense 层
concat_dense_inputs = Concatenate(axis=1)(dense_inputs)  # ?, 13
# 然后连上输出为1个单元的全连接层，表示对 dense 变量的加权求和
fst_order_dense_layer = Dense(1)(concat_dense_inputs)  # ?, 1

到这里，分别完成了对Dense特征和Sparse特征的加权求和。最后将二者的结果再求和：

linear_part = Add()([fst_order_dense_layer, fst_order_sparse_layer])

一阶的最终结果是：linear_part

二阶（交叉）特征

$$\sum _{i=1}^n\sum _{j=i+1}^n⟨{\mathbf{v}}_i,{\mathbf{v}}_j⟩x_i{x}_j=\frac{1}{2}\sum _{f=1}^k\left({\left(\sum _{i=1}^n{v}_{i,f}{x}_i\right)}^2-\sum _{i=1}^n{v}_{i,f}^2{x}_i^2\right)$$

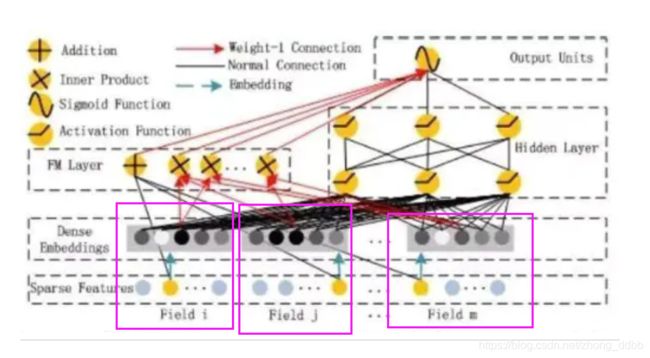
在进行二阶特征组合之前，每个sparse特征需要先进行embedding，如下图的紫色方框所示:

代码如下：

# embedding size
k = 8

# 只考虑sparse的二阶交叉
sparse_kd_embed = []
for i, _input in enumerate(sparse_inputs):
    f = sparse_feats[i]
    # 注意，nan 不会被 nunique() 所统计
    voc_size = total_data[f].nunique()
    reg = tf.keras.regularizers.l2(0.7)
    _embed = Embedding(voc_size, k, embeddings_regularizer=reg)(_input)
    sparse_kd_embed.append(_embed)

对embedding的结果FM二阶特征计算。步骤如下：

（1）首先进行 ${\left({\sum }_{i=1}^n{v}_{i,f}{x}_i\right)}^2$,其中$x_i=1$故可以忽略，这部分的计算如下：

# 1.将所有 sparse 特征 (?, 1, k)的embedding拼接起来，
# 得到 (?, n, k)的矩阵，其中n为特征数，k为embedding大小
concat_sparse_kd_embed = Concatenate(axis=1)(sparse_kd_embed)  # ?, n, k

# 2.先求和再平方
sum_kd_embed = Lambda(lambda x: K.sum(x, axis=1))(concat_sparse_kd_embed)  # ?, k
square_sum_kd_embed = Multiply()([sum_kd_embed, sum_kd_embed])  # ?, k

(2) 然后是的计算${\sum }_{i=1}^n{v}_{i,f}^2{x}_i^2$

# 3.先平方再求和
square_kd_embed = Multiply()([concat_sparse_kd_embed, concat_sparse_kd_embed]) # ?, n, k
sum_square_kd_embed = Lambda(lambda x: K.sum(x, axis=1))(square_kd_embed)  # ?, k

(3) 最后是完整公式的计算:

# 4.相减除以2
sub = Subtract()([square_sum_kd_embed, sum_square_kd_embed])  # ?, k
sub = Lambda(lambda x: x*0.5)(sub)  # ?, k
snd_order_sparse_layer = Lambda(lambda x: K.sum(x, axis=1, keepdims=True))(sub)  # ?, 1

二阶的最终结果是：snd_order_sparse_layer

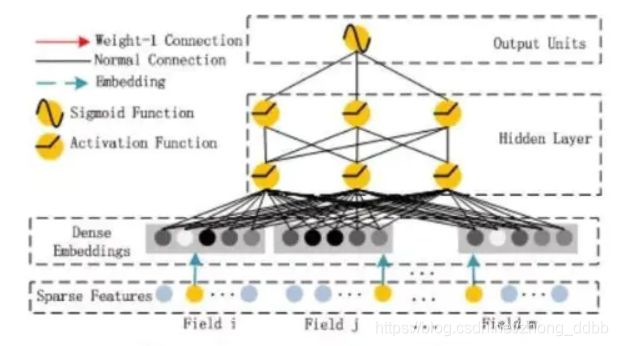
DNN部分

这部分主要是全连接层为主，用于实现高阶的特征组合，这一部分的输入是将sparse_feat的embedding的结果进行展开。

flatten_sparse_embed = Flatten()(concat_sparse_kd_embed)  # ?, n*k
fc_layer = Dropout(0.5)(Dense(256, activation='relu')(flatten_sparse_embed))  # ?, 256
fc_layer = Dropout(0.3)(Dense(256, activation='relu')(fc_layer))  # ?, 256
fc_layer = Dropout(0.1)(Dense(256, activation='relu')(fc_layer))  # ?, 256
fc_layer_output = Dense(1)(fc_layer)  # ?, 1

组合FM和DNN

接下来就是将 FM 和 DNN 部分的输出组合起来，构成完整的模型：

output_layer = Add()([linear_part, snd_order_sparse_layer, fc_layer_output])
output_layer = Activation("sigmoid")(output_layer)

model = Model(dense_inputs+sparse_inputs, output_layer)
model.compile(optimizer="adam", 
              loss="binary_crossentropy", 
              metrics=["binary_crossentropy", tf.keras.metrics.AUC(name='auc')])

模型训练

train_data = total_data.loc[:500000-1]
valid_data = total_data.loc[500000:]

train_dense_x = [train_data[f].values for f in dense_feats]
train_sparse_x = [train_data[f].values for f in sparse_feats]
train_label = [train_data['label'].values]

val_dense_x = [valid_data[f].values for f in dense_feats]
val_sparse_x = [valid_data[f].values for f in sparse_feats]
val_label = [valid_data['label'].values]

model.fit(train_dense_x+train_sparse_x, 
          train_label, epochs=5, batch_size=256,
          validation_data=(val_dense_x+val_sparse_x, val_label),
         )

完整代码
数据下载地址为：数据下载地址为：链接：https://pan.baidu.com/s/1Qy3yemu1LYVtj0Wn47myHQ 提取码：pv7u

参考文章：

CTR模型TensorFlow2.0 的 DeepFM 实现与实战(附代码+数据)