pytorch lstm源代码解读
最近阅读了pytorch中lstm的源代码，发现其中有很多值得学习的地方。
首先查看pytorch当中相应的定义
\begin{array}{ll} \\
i_t = \sigma(W_{ii} x_t + b_{ii} + W_{hi} h_{t-1} + b_{hi}) \\
f_t = \sigma(W_{if} x_t + b_{if} + W_{hf} h_{t-1} + b_{hf}) \\
g_t = \tanh(W_{ig} x_t + b_{ig} + W_{hg} h_{t-1} + b_{hg}) \\
o_t = \sigma(W_{io} x_t + b_{io} + W_{ho} h_{t-1} + b_{ho}) \\
c_t = f_t \odot c_{t-1} + i_t \odot g_t \\
h_t = o_t \odot \tanh(c_t) \\
\end{array}
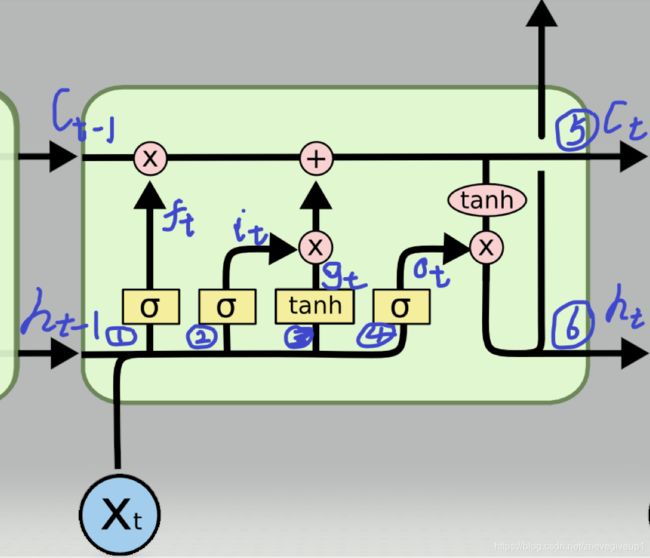
对应公式：
圈1： f t = σ ( W i f x t + b i f + W h f h t − 1 + b h f ) f_t = \sigma(W_{if} x_t + b_{if} + W_{hf} h_{t-1} + b_{hf}) ft=σ(Wifxt+bif+Whfht−1+bhf)
圈2： i t = σ ( W i i x t + b i i + W h i h t − 1 + b h i ) i_t = \sigma(W_{ii} x_t + b_{ii} + W_{hi} h_{t-1} + b_{hi}) it=σ(Wiixt+bii+Whiht−1+bhi)
圈3： g t = tanh ( W i g x t + b i g + W h g h t − 1 + b h g ) g_t = \tanh(W_{ig} x_t + b_{ig} + W_{hg} h_{t-1} + b_{hg}) gt=tanh(Wigxt+big+Whght−1+bhg)
圈4： o t = σ ( W i o x t + b i o + W h o h t − 1 + b h o ) o_t = \sigma(W_{io} x_t + b_{io} + W_{ho} h_{t-1} + b_{ho}) ot=σ(Wioxt+bio+Whoht−1+bho)
圈5： c t = f t ⊙ c t − 1 + i t ⊙ g t c_t = f_t \odot c_{t-1} + i_t \odot g_t ct=ft⊙ct−1+it⊙gt
圈6： h t = o t ⊙ tanh ( c t ) h_t = o_t \odot \tanh(c_t) ht=ot⊙tanh(ct)
调用lstm的相应代码如下：
import torch
import torch.nn as nn
bilstm = nn.LSTM(input_size=10, hidden_size=20, num_layers=2, bidirectional=True)
input = torch.randn(5, 3, 10)
h0 = torch.randn(4, 3, 20)
c0 = torch.randn(4, 3, 20)
#with open('D://test//input1.txt','w') as f:
# f.write(str(input))
#with open('D://test//h0.txt','w') as f:
# f.write(str(h0))
#with open('D://test//c0.txt','w') as f:
# f.write(str(c0))
output, (hn, cn) = bilstm(input, (h0, c0))
print('output shape: ', output.shape)
print('hn shape: ', hn.shape)
print('cn shape: ', cn.shape)
这里的input = (seq_len, batch, input_size)，h_0 (num_layers * num_directions, batch, hidden_size)，c_0 (num_layers * num_directions, batch, hidden_size)
观察初始化部分的源代码
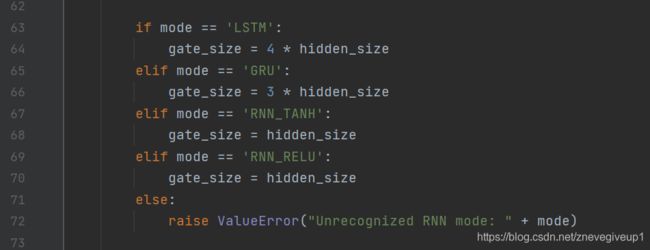可以看出这里当为lstm层的时候，gate_size = 4*hidden_size
这里当bidirectional = True时num_directions = 2,当bidirectional = False时num_directions = 1。
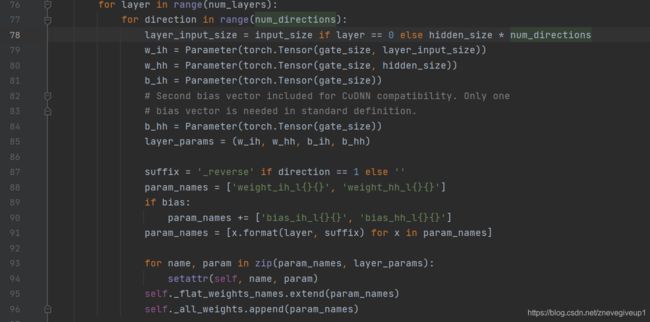self._flat_weigts_names中的数值，因为这里总共定义了两层，所以’weight_ih_l0’ = [80,10],‘weight_hh_l0’ = [80,20],‘bias_ih_l0’ = [80],‘bias_hh_l0’ = [80],‘weight_ih_l0_reverse’ = [80,10],‘weight_hh_l0_reverse’ = [80,20],‘bias_ih_l0_reverse’ = [80],‘bias_hh_l0_reverse’ = [80]
‘weight_ih_l1’ = [80,40],‘weight_hh_l1’ = [80,20],‘bias_ih_l1’ = [80],‘bias_hh_l1’ = [80]
‘weight_ih_l1_reverse’ = [80,40],‘weight_hh_l1_reverse’ = [80,20],‘bias_ih_l1_reverse’ = [80],‘bias_hh_l1_reverse’ = [80]
关于这些数组的意义回读一下之前的注释内容
这里面的weight_ih_l[k] = [80,10]，其中的80是由4hidden_size = 420得到的，这4个参数分别为W_ii,W_if,W_ig,W_io,而weight_ih_l[k]是由这四个参数拼接得来的[80,10],同理可得到对应的weight_ih_l[k],weight_hh_l[k],bias_ih_l[k],bias_hh_l[k]的相应的含义。
其中，input = [5,3,10],h0 = [4,3,20],c0 = [4,3,20]
对应的lstm结构图如下所示
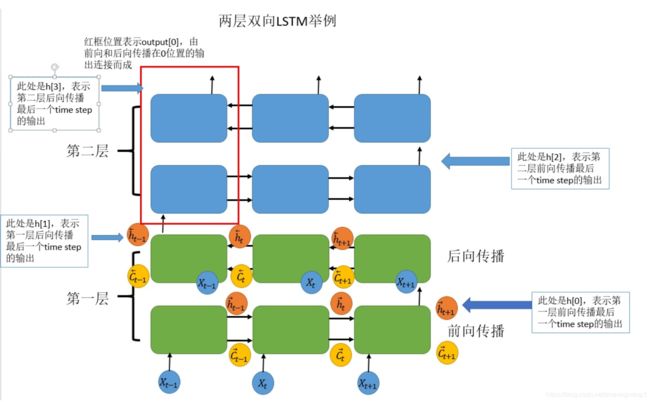h0中的[4,3,20]中的h0[0],h0[1],h0[2],h0[3]分别对应着h[0],h[1],h[2],h[3],每一个的shape都等于[3,20]
同理c0的原理一致。
对于公式进行分析
对于第一层的内容：
公式1： f t = σ ( W i f [ 20 , 10 ] x t + b i f [ 20 ] + W h f [ 20 , 20 ] h t − 1 + b h f [ 20 ] ) f_t = \sigma(W_{if}[20,10] x_t + b_{if}[20] + W_{hf}[20,20] h_{t-1} + b_{hf}[20]) ft=σ(Wif[20,10]xt+bif[20]+Whf[20,20]ht−1+bhf[20])
公式2： i t = σ ( W i i [ 20 , 10 ] x t + b i i [ 20 ] + W h i [ 20 , 20 ] h t − 1 + b h i [ 20 ] ) i_t = \sigma(W_{ii}[20,10] x_t + b_{ii}[20] + W_{hi}[20,20] h_{t-1} + b_{hi}[20]) it=σ(Wii[20,10]xt+bii[20]+Whi[20,20]ht−1+bhi[20])
公式3： g t = tanh ( W i g [ 20 , 10 ] x t + b i g [ 20 ] + W h g [ 20 , 20 ] h t − 1 + b h g [ 20 ] ) g_t = \tanh(W_{ig}[20,10] x_t + b_{ig}[20] + W_{hg}[20,20] h_{t-1} + b_{hg}[20]) gt=tanh(Wig[20,10]xt+big[20]+Whg[20,20]ht−1+bhg[20])
公式4： o t = σ ( W i o [ 20 , 10 ] x t + b i o [ 20 ] + W h o [ 20 , 20 ] h t − 1 + b h o [ 20 ] ) o_t = \sigma(W_{io}[20,10] x_t + b_{io}[20] + W_{ho}[20,20] h_{t-1} + b_{ho}[20]) ot=σ(Wio[20,10]xt+bio[20]+Who[20,20]ht−1+bho[20])
公式5： c t = f t [ 20 , 20 ] ⊙ c t − 1 [ 20 , 20 ] + i t [ 20 , 20 ] ⊙ g t [ 20 , 20 ] c_t = f_t[20,20] \odot c_{t-1}[20,20] + i_t[20,20] \odot g_t[20,20] ct=ft[20,20]⊙ct−1[20,20]+it[20,20]⊙gt[20,20]
公式6： h t = o t [ 20 , 20 ] ⊙ tanh ( c t ) [ 20 , 20 ] h_t = o_t[20,20] \odot \tanh(c_t)[20,20] ht=ot[20,20]⊙tanh(ct)[20,20]
对于第二层的内容：
公式1： f t = σ ( W i f [ 20 , 40 ] x t + b i f [ 20 ] + W h f [ 20 , 20 ] h t − 1 + b h f [ 20 ] ) f_t = \sigma(W_{if}[20,40] x_t + b_{if}[20] + W_{hf}[20,20] h_{t-1} + b_{hf}[20]) ft=σ(Wif[20,40]xt+bif[20]+Whf[20,20]ht−1+bhf[20])
公式2： i t = σ ( W i i [ 20 , 40 ] x t + b i i [ 20 ] + W h i [ 20 , 20 ] h t − 1 + b h i [ 20 ] ) i_t = \sigma(W_{ii}[20,40] x_t + b_{ii}[20] + W_{hi}[20,20] h_{t-1} + b_{hi}[20]) it=σ(Wii[20,40]xt+bii[20]+Whi[20,20]ht−1+bhi[20])
公式3： g t = tanh ( W i g [ 20 , 40 ] x t + b i g [ 20 ] + W h g [ 20 , 20 ] h t − 1 + b h g [ 20 ] ) g_t = \tanh(W_{ig}[20,40] x_t + b_{ig}[20] + W_{hg}[20,20] h_{t-1} + b_{hg}[20]) gt=tanh(Wig[20,40]xt+big[20]+Whg[20,20]ht−1+bhg[20])
公式4： o t = σ ( W i o [ 20 , 40 ] x t + b i o [ 20 ] + W h o [ 20 , 20 ] h t − 1 + b h o [ 20 ] ) o_t = \sigma(W_{io}[20,40] x_t + b_{io}[20] + W_{ho}[20,20] h_{t-1} + b_{ho}[20]) ot=σ(Wio[20,40]xt+bio[20]+Who[20,20]ht−1+bho[20])
公式5： c t = f t [ 20 , 20 ] ⊙ c t − 1 [ 20 , 20 ] + i t [ 20 , 20 ] ⊙ g t [ 20 , 20 ] c_t = f_t[20,20] \odot c_{t-1}[20,20] + i_t[20,20] \odot g_t[20,20] ct=ft[20,20]⊙ct−1[20,20]+it[20,20]⊙gt[20,20]
公式6： h t = o t [ 20 , 20 ] ⊙ tanh ( c t ) [ 20 , 20 ] h_t = o_t[20,20] \odot \tanh(c_t)[20,20] ht=ot[20,20]⊙tanh(ct)[20,20]