XGBoost算法
- XGBoost是陈天奇等人开发的一个开源机器学习项目,高效地实现了GBDT算法并进行了算法和工程上的许多改进,被广泛应用在Kaggle竞赛及其他许多机器学习竞赛中并取得了不错的成绩。
- • XGBoost的基学习器除了可以是CART(这个时候就是GBDT)也可以是线性分类器,而GBDT只能是CART。
• XGBoost的目标函数的近似用了二阶泰勒展开,模型优化效果更好。
• XGBoost在代价函数中加入了正则项,用于控制模型的复杂度(正则项的方式不同,如果你仔细点话,GBDT是一种类似于缩减系数,而XGBoost类似于L2正则化项)。
• XGBoost借鉴了随机森林的做法,支持特征抽样,不仅防止过拟合,还能减少计算
• XGBoost工具支持并行化
• 综合来说Xgboost的运算速度和算法精度都会优于GBDT
XGBoost库的使用
- 读取数据xgb.Dmatrix()
设置参数param={}
训练模型bst = xgb.train(param)
预测结果bst.predict()
模型评估:预测之后需要重新导入模型评估结果进行评估
- 导入相关待使用的库
from xgboost import XGBRegressor as XGBR
from sklearn.ensemble import RandomForestRegressor
from sklearn.linear_model import LinearRegression
from sklearn import datasets
from sklearn.model_selection import KFold,cross_val_score,train_test_split
from sklearn.metrics import mean_squared_error
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from time import time
import datetime
- 导入boston房价数据集用做模型训练和预测,并切分好训练集和测试集
data = datasets.load_boston()
X_data,y_data = data.data,data.target
X_data.shape
>> (506, 13)
X_train,X_test,y_train,y_test = train_test_split(X_data,y_data,test_size = 0.3,random_state = 420)
reg = XGBR(n_estimators=100).fit(X_train,y_train)
reg.predict(X_test)
>>
array([ 8.165384 , 21.919355 , 29.843645 , 11.874415 , 8.833874 ,
20.698246 , 15.456877 , 15.544203 , 15.273806 , 13.444421 ,
22.130966 , 35.072395 , 21.383947 , 27.477697 , 20.449163 ,
10.434615 , 19.13851 , 24.973454 , 23.284975 , 23.22411 ,
17.86431 , 17.218367 , 25.284815 , 20.962675 , 20.506361 ,
16.18782 , 21.71437 , 31.687273 , 22.739857 , 15.976351 ,
37.61867 , 20.701538 , 21.191647 , 23.53703 , 23.374733 ,
24.682228 , 16.27922 , 24.404453 , 16.918646 , 34.06889 ,
18.060398 , 21.352114 , 37.74781 , 17.90909 , 14.035863 ,
28.243176 , 46.44803 , 14.748789 , 10.719417 , 35.26486 ,
25.46181 , 21.976503 , 20.583235 , 49.3701 , 26.799538 ,
26.286161 , 17.937538 , 20.566235 , 16.813719 , 18.816374 ,
14.940857 , 22.213655 , 19.239632 , 30.246548 , 27.522081 ,
18.951006 , 19.352182 , 15.716684 , 22.732222 , 19.14629 ,
29.943521 , 43.593327 , 29.910528 , 22.987352 , 20.6698 ,
23.078789 , 42.398773 , 26.09842 , 21.91394 , 20.648191 ,
19.003222 , 46.083096 , 22.536583 , 8.913077 , 26.097902 ,
23.269075 , 17.367735 , 21.026497 , 19.989 , 11.0460415,
20.702105 , 15.85642 , 41.646564 , 33.36533 , 22.891464 ,
10.986401 , 15.041652 , 20.024511 , 8.583407 , 10.585413 ,
31.516539 , 17.450106 , 24.464012 , 23.16676 , 31.216547 ,
41.60174 , 21.293688 , 8.508124 , 22.987352 , 14.409528 ,
45.271053 , 21.575006 , 22.017088 , 22.765581 , 18.600304 ,
27.935238 , 24.568512 , 17.984907 , 44.804962 , 17.453247 ,
24.616978 , 22.51571 , 16.867426 , 16.851673 , 15.302382 ,
22.844278 , 32.24536 , 9.803618 , 21.071335 , 19.696089 ,
16.056892 , 19.578579 , 9.987525 , 28.184805 , 29.464226 ,
20.240805 , 19.482244 , 15.280221 , 9.401806 , 17.187815 ,
42.554493 , 16.713844 , 23.872856 , 19.95768 , 30.148867 ,
20.396807 , 13.163115 , 40.93572 , 25.202625 , 21.823097 ,
14.690604 , 26.191984 ], dtype=float32)
reg.score(X_test,y_test)
>> 0.9197580267581366
- 查看每个特征对模型的贡献,他们的总和是1,数值越大说明这个特征对模型的分类贡献越大
reg.feature_importances_
>>
array([0.02474326, 0.00233919, 0.00895177, 0.01757721, 0.04847462,
0.25909728, 0.0120366 , 0.0429231 , 0.01358514, 0.02558688,
0.04455473, 0.01763431, 0.48249587], dtype=float32)
# 使用交叉验证评估模型效果,交叉验证中导入的是没有经过训练的模型
reg = XGBR(n_estimators=100,silent=True) ## silent 会打印运行过程
#如果开启参数slient:在数据巨大,预料到算法运行会非常缓慢的时候可以使用这个参数来监控模型的训练进度
cross_val_score(reg,X_train,y_train,cv=5).mean()
>> 0.8017863029875325
下面先定义一个函数,用作画各个参数与模型训练准确率和测试准确率的学习曲线,观测XGB的各个参数对模型的影响,用此方法找出XGB模型的每个参数的最优值
def plot_learing_curve(estimators,title,X,y,
ax = None,
ylim = None,
cv = None,
n_jobs = None):
from sklearn.model_selection import learning_curve
import matplotlib.pyplot as plt
import numpy as np
train_sizes,train_scores,test_scores = learning_curve(
estimators,X,y,
shuffle=True, cv = cv,
n_jobs = n_jobs)
if ax == None:
ax = plt.gca()
else:
ax = plt.figure()
ax.set_title(title)
ax.set_xlabel('Training examples')
ax.set_ylabel('Score')
ax.plot(train_sizes,np.mean(train_scores,axis = 1), 'o-',c ='r',label='Training score')
ax.plot(train_sizes,np.mean(test_scores,axis = 1), 'o-',c ='g',label='Test score')
ax.grid()
ax.legend()
return ax
cv = KFold(n_splits=5,shuffle=True, random_state=42) ## shuffle 表示把数据集打乱
plot_learing_curve(XGBR(n_estimators = 100,random_state = 42,silent = True),"XGB",X_train,y_train,cv= cv)
plt.show()
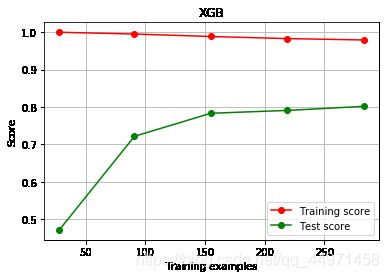
## 绘制n_estimators的学习曲线
axis_x = range(10,1010,50)
rs = [] ## 储存R^2
for i in axis_x:
reg = XGBR(n_estimators=i,random_state=42,silent = True)
rs.append(cross_val_score(reg,X_train,y_train,cv = cv).mean())
print(axis_x[rs.index(max(rs))] , max(rs))
plt.figure(figsize = (20,8))
plt.plot(axis_x,rs,c='r',label = 'XGB')
plt.legend()
plt.show()
>> 660 0.8046775284172915

- 绘制训练轮数与R2拟合优度之间的超参数曲线,看看XGB模型在训练多少轮的时候效果相当来说最好
axis_x = range(50,1050,50)
rs = []
var = []
ge = []
for i in axis_x:
reg = XGBR(n_estimators=i,random_state=42,silent = True)
cv_result = cross_val_score(reg,X_train,y_train,cv = cv)
rs.append(cv_result.mean()) ## 记录1-偏差,也就是R^2
var.append(cv_result.var()) ## 记录方差
ge.append((1 - cv_result.mean())**2 + cv_result.var()) ## 计算泛化误差的可控部分
## 打印R^2最高所对应的参数取值,并打印这个参数下的方差
print(axis_x[rs.index(max(rs))],max(rs),var[rs.index(max(rs))])
## 打印方差最低是对应的参数取值,并打印这个参数下的R^2
print(axis_x[var.index(min(var))],rs[var.index(min(var))],min(var))
## 打印泛化误差可控部分的参数取值,并打印这个参数下的R^2,方差以及泛化误差的可控部分
print(axis_x[ge.index(min(ge))],rs[ge.index(min(ge))],var[ge.index(min(ge))],min(ge))
plt.plot(axis_x,rs,c='r',label='XGB')
plt.legend()
plt.show()
>>
650 0.80476050359201 0.01053673846018678
50 0.7857724708830981 0.009072727885598212
150 0.8032842414878519 0.009747694343514357 0.04844478399052411
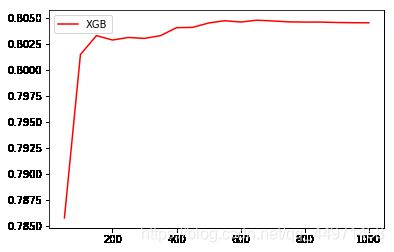
- 可以看到模型在训练轮数为100-200之间有一个极大值,也就是在这个范围内有一个比较好的效果,而且在600轮左右效果最好。下面我们找出100-200之间的最优轮数,缩小这个超参数的轮数间距,再训练一次看看效果。
axis_x = range(100,200,10)
rs = []
var = []
ge = []
for i in axis_x:
reg = XGBR(n_estimators=i,random_state=42,silent = True)
cv_result = cross_val_score(reg,X_train,y_train,cv = cv)
rs.append(cv_result.mean()) ## 记录1-偏差,也就是R^2
var.append(cv_result.var()) ## 记录方差
ge.append((1 - cv_result.mean())**2 + cv_result.var()) ## 计算泛化误差的可控部分
## 打印R^2最高所对应的参数取值,并打印这个参数下的方差
print(axis_x[rs.index(max(rs))],max(rs),var[rs.index(max(rs))])
## 打印方差最低是对应的参数取值,并打印这个参数下的R^2
print(axis_x[var.index(min(var))],rs[var.index(min(var))],min(var))
## 打印泛化误差可控部分的参数取值,并打印这个参数下的R^2,方差以及泛化误差的可控部分
print(axis_x[ge.index(min(ge))],rs[ge.index(min(ge))],var[ge.index(min(ge))],min(ge))
rs = np.array(rs)
var = np.array(var)*0.01
plt.plot(axis_x,rs,c='r',label='XGB')
plt.plot(axis_x,rs + var,c='b',linestyle = '-.')
plt.plot(axis_x,rs-var,c='b',linestyle = '-.')
plt.legend()
plt.show()
>>
180 0.8038787848970184 0.00959321570484315
180 0.8038787848970184 0.00959321570484315
180 0.8038787848970184 0.00959321570484315 0.04805674671831314
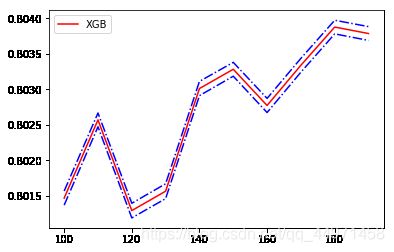
- 可以看到训练轮数在180轮左右效果最好,R2拟合优度达到了92.3%,你也可以继续缩小轮数间距,直到找到那个最优的轮数,这里我们就跳过。
print(XGBR(n_estimators = 100,random_state = 42).fit(X_train,y_train).score(X_test,y_test))
print(XGBR(n_estimators = 660,random_state = 42).fit(X_train,y_train).score(X_test,y_test))
print(XGBR(n_estimators = 180,random_state = 42).fit(X_train,y_train).score(X_test,y_test))
>>
[14:22:12] WARNING: C:/Jenkins/workspace/xgboost-win64_release_0.90/src/objective/regression_obj.cu:152: reg:linear is now deprecated in favor of reg:squarederror.
0.9197580267581366
[14:22:13] WARNING: C:/Jenkins/workspace/xgboost-win64_release_0.90/src/objective/regression_obj.cu:152: reg:linear is now deprecated in favor of reg:squarederror.
0.9208745746309475
[14:22:13] WARNING: C:/Jenkins/workspace/xgboost-win64_release_0.90/src/objective/regression_obj.cu:152: reg:linear is now deprecated in favor of reg:squarederror.
0.9231068620728082
- 在选择训练轮数n_estimators最优值为180轮时,继续对另外的参数进行调优
## 参learning_rate,学习率或者步长
## 首先定义一个评分函数,这个评分函数能够帮我们直接打印X_train上的交叉验证结果
def regassess(reg,X_train,y_train,cv,scoring = ["r2"],show=True):
score = []
for i in range(len(scoring)):
if show:
print("{}:{:.2f}".format(scoring[i],cross_val_score(reg,X_train,y_train,
cv=cv,scoring=scoring[i]).mean()))
score.append(cross_val_score(reg,X_train,y_train,
cv = cv,scoring = scoring[i]).mean())
return score
reg = XGBR(n_estimators=180 , random_state=42,silent=True)
regassess(reg,X_train,y_train,cv,scoring=["r2","neg_mean_squared_error"])
>> r2:0.80
neg_mean_squared_error:-13.48
[0.8038787848970184, -13.482301822063182]
## 观察eta怎么影响模型的结果(learning_rate)
from time import time
import datetime
for i in [0,0.2,0.5,1]:
time0 = time()
reg = XGBR(n_estimators=180,random_state=42,learning_rate=i,silent=True)
print("learning_rate = {}".format(i))
regassess(reg,X_train,y_train,cv,scoring=['r2','neg_mean_squared_error'])
print(datetime.datetime.fromtimestamp(time() - time0).strftime("%M:%S:%f"))
print("*"*100)
>> learning_rate = 0
r2:-6.76
neg_mean_squared_error:-567.55
00:01:684057
****************************************************************************************************
learning_rate = 0.2
r2:0.81
neg_mean_squared_error:-13.42
00:01:457285
****************************************************************************************************
learning_rate = 0.5
r2:0.81
neg_mean_squared_error:-13.20
00:01:485940
****************************************************************************************************
learning_rate = 1
r2:0.72
neg_mean_squared_error:-19.12
00:01:445907
****************************************************************************************************
- 可以看出在学习率是0,0.2,0.5,1这几个学习率中,learning_rate = 0.5的效果是最优的,下面我们缩小学习率间距多训练一些情况看看具体learning_rate是多少时效果最好。
axisx = np.arange(0.05,1,0.05)
rs = []
te = []
for i in axisx:
reg = XGBR(n_estimators=180,random_state=42,learning_rate=i,silent=True)
score = regassess(reg,X_train,y_train,cv,scoring=['r2','neg_mean_squared_error'],show = False)
test = reg.fit(X_train,y_train).score(X_test,y_test)
rs.append(score[0])
te.append(test)
print(axisx[rs.index(max(rs))],max(rs))
plt.figure(figsize=(20,8))
plt.xlabel("learning_rate")
plt.plot(axisx,te,c='r',label = 'XGB')
plt.plot(axisx,rs,c='g',label = 'XGB')
plt.legend()
plt.show()
>> 0.55 0.8125604372670463
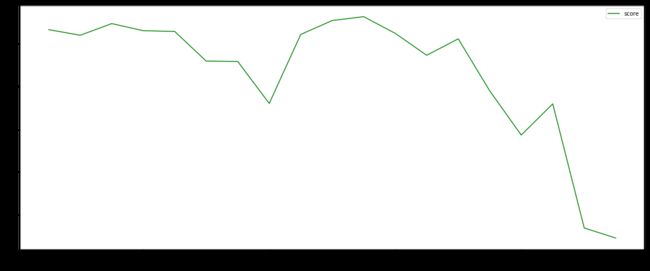
- 可以看到learning_rate = 0.55时模型效果最好
我们同样可以用这样的超参数曲线方法去找出XGBoost的其他参数的最优值,组合所有的最优参数就可以训练处最优的模型




