cs224w 图神经网络 学习笔记（六）Spectral Clustering 谱聚类

课程链接：CS224W: Machine Learning with Graphs
课程视频：【课程】斯坦福 CS224W: 图机器学习 (2019 秋 | 英字)

谱聚类是一种基于图论的聚类方法，通过对样本数据的拉普拉斯矩阵的特征向量进行聚类，从而达到对样本数据聚类的母的。谱聚类可以理解为将高维空间的数据映射到低维，然后在低维空间用其它聚类算法（如KMeans）进行聚类。

1 谱聚类分析的三个基本步骤

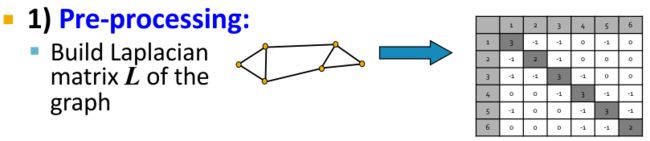
（1）Pre-processing 预处理

• Construct a matrix representation of the graph 构造图的矩阵表示

（2）Decomposition 分解

• Compute eigenvalues and eigenvectors of the matrix 计算矩阵的特征值和特征向量
• Map each point to a lower-dimensional representation based on one or more eigenvectors 将每个点映射到一个低维向量

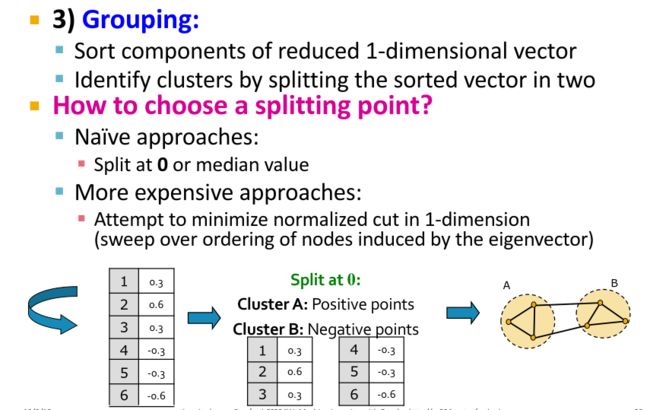
（3）Grouping 聚类

• Assign points to two or more clusters, based on the new representation 根据降维后的向量进行分组

2 问题的引入——Graph Partitioning 图的分割

在讲到谱聚类之前，我们先来看一下我们要解决的问题。

给定一张无向图$G(V,E)$中，谱聚类的任务可以定义为Bi-partitioning task，就是将图$G$中的节点分为两个不相交的集合$A$和$B$。

那么，现在有两个问题需要解决：

• How can we define a “good” partition of $G$? 怎么定义图$G$的分割是好的？
  好的分割主要由两个因素决定 （What makes a good partition?）：
  – Maximize the number of within-group connections 组内成员的连接尽可能的多
  – Minimize the number of between-group connections 组间成员的连接尽可能的少

• How can we efficiently identify such a partition? 怎样快速有效地识别这些分割？
  这就需要一些评价指标。

3 图分割的评价指标

（1）Cut 和 Minimum-cut

Cut: Set of edges with one endpoint in each group.

第一个评价指标称作Cut，也就是将图的分割的情况表示为两个分割块的Edge cut的函数（Express partitioning objectives as a function of the “edge cut” of the partition）
$$cut(A,B)=\sum _{i\in A,j\in B}{\omega }_{ij}$$

如果是有权图，${\omega }_{ij}$为边的权值；如果是无权图，${\omega }_{ij}$为$\{0,1\}$，连接为1，不连接为0。

下面就是一个例子：

前面说到，好的分割的标准之一就是不同分割块的成员之间的连接尽可能地少。所以使用cut这个标准来衡量图分割的目标就是找到Minimum-cut，也就是$arg{\min }_{A,B}cut(A,B)$。

但是，cut这个指标只考虑了外部连接，没有考虑分割块内部的连接。这样会带来一个问题，就是最小的不一定是最优的，比如：

在此基础上，[Shi-Malik, ’97]提出了一个新的衡量图分割的指标Conductance。

（2）Conductance

Conductance的定义式如下：

与Cut相比，Conductance考虑了分割块的“体积”，使得分割后得到的不同的块更加平衡。但是，去得到最好的Conductance值是一个NP难度的问题。Spectral Graph Partitioning是一种得到近似优化值的方法。

4 图的谱——Spectral Graph Partitioning

• 设$A$为无向图$G$的邻接矩阵，$a_{ij}=\{0,1\}$。
• 设$n$维向量$x=\{x_1,x_2,\cdots ,x_n\}$为图$G$中$n$个节点的标签/值（特征向量）。

则：
$$A\cdot x=\left[\begin{array}{ccc}{a}_{11}& \cdots & a_{1n}\\ ⋮& & ⋮\\ a_{n1}& \cdots & a_{nn}\end{array}\right]\left[\begin{array}{c}{x}_1\\ ⋮\\ x_n\end{array}\right]=\left[\begin{array}{c}{y}_1\\ ⋮\\ y_n\end{array}\right]$$

$A\cdot x$有什么含义呢？我们通过线性代数的知识可以知道，$y_i={\sum }_{j=1}^n{A}_{ij}{x}_j={\sum }_{(i,j)\in E}{x}_j$，也就是说，$y_i$计算的是节点$i$的邻居的标签之和。

令$A\cdot x=\lambda \cdot x$，可以得到特征值（eigenvalues）${\lambda }_i$和相应的特征向量（eigenvectors）$x^{(i)}$。对于图$G$来说，它的**谱（Spectrum）**定义为其一组特征向量$x^{(i)}$，且这组特征向量满足其对应的特征值为$\Lambda =\{{\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n\}$，其中${\lambda }_1\le {\lambda }_2\le \cdots \le {\lambda }_n$。

① 设$G$为一个所有节点的度为$d$的连通图（d-regular graph），设特征向量为$x=(1,1,\cdots ,1)$，则$d$为图$G$的邻接矩阵$A$的特征值，且为最大特征值，即${\lambda }_n=d$。【老师的PPT里面给了证明】

② 设图$G$为两个不连通的d-regular graph组成，如下图所示。此时${\lambda }_{n-1}={\lambda }_n=d$

推广：

• 如果d-regular graph是连通的，那么我们知道$x_n=(1,1,\cdots ,1)$是图的一个特征向量。
• 由于邻接矩阵$A$是实对称矩阵，属于矩阵$A$不同特征值的特征向量是相互正交的，所以
  对于剩下的特征向量来说，$x_n\cdot x_{n-1}=0$，即${\sum }_i{x}_n[i]\cdot x_{n-1}[i]={\sum }_i{x}_{n-1}[i]=0$。也就是说，第二大特征向量$x_{n-1}$将剩下的点分成了两部分，$x_{n-1}>0$的和$x_{n-1}<0$的。

这样一来，我们就有了将图的节点进行分割的方法。并且，将图和线性代数（矩阵）结合，提供了计算机参与的切入点。

5 图的矩阵（Matrix representations）

（1）邻接矩阵 Adjacency matrix $A$

邻接矩阵 $A$ 是 $n\times n$ 的矩阵，$A=[a_{ij}]$，如果节点$i$和节点$j$有边相连，则$a_{ij}=1$。

邻接矩阵 $A$ 具有以下三个特点：

• Symmetric matrix 对称矩阵
• Has $n$ real eigenvalues 有$n$个实特征值
• Eigenvectors are real-valued and orthogonal 特征向量均为实向量，且不同特征值对应的特征向量正交

（2）度矩阵 Degree Matrix $D$

度矩阵 $D$ 是一个 $n\times n$ 的对角矩阵，$D=[d_{ii}]$。

（3）Laplacian matrix $L$

定义：$L=D-A$

Laplacian matrix $L$有以下属性：

• 令$x=(1,1,\cdots ,1)$，则$L\cdot x=0$，因此（最小）特征值为$\lambda ={\lambda }_1=0$。那么对于特征值${\lambda }_2$对应的特征向量$x$来说，$x$是一个单位向量，即$x^{T}x={\sum }_i{x}_i^2=1$；且$x^T{\lambda }_1={\sum }_i{x}_i\cdot 1={\sum }_i{x}_i=0$。
• Eigenvalues are non-negative real numbers 特征值均为非负实数
• Eigenvectors are real (and always orthogonal) 特征向量均为实向量，且不同特征值对应的特征向量正交
• 对所有的$x$，$x^{T}Lx={\sum }_{ij}{L}_{ij}{x}_i{x}_j\ge 0$。那么，我们来看一下图$G$的$x^{T}Lx$是什么含义呢？
  $$\begin{array}{rl}{x}^{T}Lx& =\sum _{i,j=1}^n{L}_{ij}{x}_i{x}_j=\sum _{i,j=1}^n(D_{ij}-A_{ij})x_i{x}_j\\ & =\sum _{i,j=1}^n{D}_{ij}{x}_j^2-\sum _{(i,j)\in E}2x_i{x}_j\\ & =\sum _{(i,j)\in E}{x}_i^2+x_j^2-2x_i{x}_j\\ & =\sum _{(i,j)\in E}(x_i-x_j{)}^2\end{array}$$
• $L$可以写作 $L=N^{T}N$

引理：对于对称矩阵$M$，特征值
$${\lambda }_2=\underset{x:x^T{\omega }_1=0}{\min }\frac{x^{T}Mx}{x^{T}x}$$
其中${\omega }_1$是特征值${\lambda }_1$对应的特征向量。
（关于这个引理的证明在老师的课件里面有）

那么对于Laplacian矩阵
$${\lambda }_2=\underset{x:{\sum }_i{x}_i=0}{\min }\frac{x^{T}Lx}{x^{T}x}=\underset{x:{\sum }_i{x}_i=0}{\min }\frac{{\sum }_{(i,j)\in E}(x_i-x_j{)}^2}{{\sum }_i{x}_i^2}=\underset{x:{\sum }_i{x}_i=0}{\min }\sum _{(i,j)\in E}(x_i-x_j{)}^2$$

因为${\sum }_i{x}_i=0$，所以所求的解有正有负，而最理想的情况就是使尽可能少的边经过“0轴”。

6 Find Optimal Cut

我们还是回到最开始的问题——怎样得到图的最佳分割？

[Fiedler '73]提出了一种寻找最佳切分点的方案：

参考：【CS224W课程笔记】Spectral Clustering

7 Spectral Clustering Algorithms 谱聚类算法（详细）

最后，我们再来回顾一下谱聚类算法的三个步骤：

（1）Pre-processing 预处理

• Construct a matrix representation of the graph 构造图的矩阵表示
  

（2）Decomposition 分解

• Compute eigenvalues and eigenvectors of the matrix 计算矩阵的特征值和特征向量
• Map each point to a lower-dimensional representation based on one or more eigenvectors 将每个点映射到一个低维向量
  

（3）Grouping 聚类

• Assign points to two or more clusters, based on the new representation 根据降维后的向量进行分组

下面是一些案例：

例1	例2	例3

8. K-way Spectral Clustering

怎样将图上的节点分成$k$类呢？有两种方法：

（1） 递归 Recursive bi-partitioning [Hagen et al., ’92]

递归利用二分算法，将图进行划分。但是递归方法效率比较低，且比较不稳定。

（2）Cluster multiple eigenvectors [Shi-Malik, ’00]

通过特征向量进行聚类。该方法目前比较常用，且效果较好。

这种方法有以下几个优点：

• Approximates the optimal cut 更接近最优分割——Can be used to approximate optimal k-way normalized cut
• Emphasizes cohesive clusters 着重于更凝聚的类别——①Increases the unevenness in the distribution of the data 考虑了数据的不均匀性 ②Associations between similar points are amplified, associations between dissimilar points are attenuated 相似点之间的关联被放大，不同点之间的关联被减弱 ③The data begins to “approximate a clustering” “近似聚类”

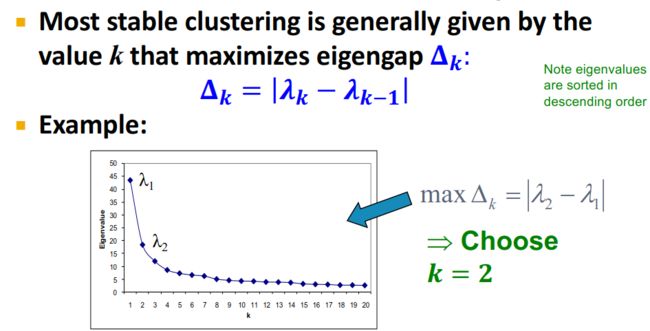
那么，怎么选择$k$呢？——How to select $k$？——通过两个连续的特征值之间的差来确定。

9. 拓展：基于motif的谱聚类 Motif-based Spetural Clustering

前面讲到的都是基于两个节点之间的关系的聚类，那么，如果我们想要基于Motif进行聚类呢？比如说下面这张图，我们给定一个图结构，并给定不同的Motif结构，就可以得到不同的聚类结果。

我们可以将Conductance的定义进行相应的推广：

下面是一个计算的例子。因为分割线$S$经过一个Motif，且Motif类中包含10个节点，可以知道${\varphi }_M(S)=\frac{1}{10}$。

类似的，问题就变成了给定图$G$和Motif结构，找到分割方式使得${\varphi }_M(S)$最小。同样的，需要通过近似算法——Motif Spectral Clustering来得到最优结果。

同样的，近似算法分为三步：

（1）预处理 Pre-processing

定义矩阵$W_{ij}^{(M)}$，其中$w_{ij}^{(M)}$表示图$G$中的边$(i,j)$在给定的Motif结构$M$中参与的次数。下图是一个例子：

用矩阵形式表示：

（2） Decomposition 分解

第二步是分解，定义度矩阵$D_{ij}^{(M)}={\sum }_j{w}_{ij}^{(M)}$，定义拉布拉斯矩阵$L^{(M)}=D^{(M)}-W^{(M)}$，计算特征值与特征向量$L^{(M)}x={\lambda }_{2}x$，由得到的特征向量$x$来对图进行分割。

（3）Grouping 分组

这一步和之前的谱聚类方法类似。