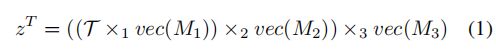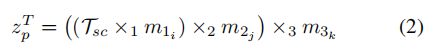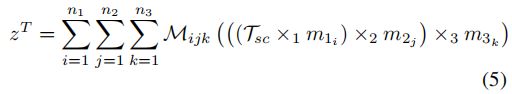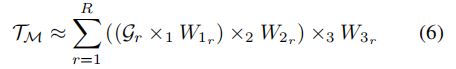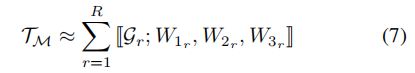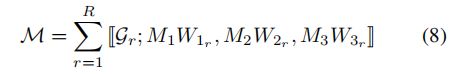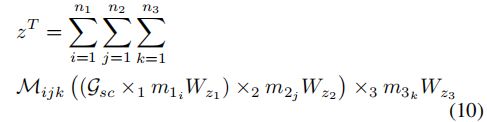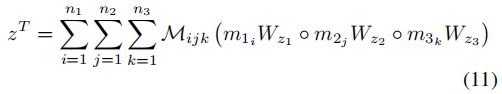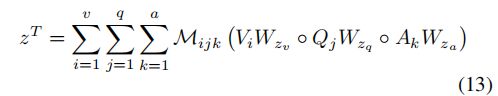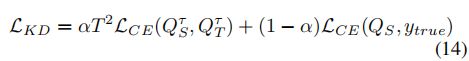目录
一、文献摘要介绍
二、网络框架介绍
三、实验分析
四、结论
这是视觉问答论文阅读的系列笔记之一,本文有点长,请耐心阅读,定会有收货。如有不足,随时欢迎交流和探讨。
一、文献摘要介绍
In Visual Question Answering (VQA), answers have a great correlation with question meaning and visual contents. Thus, to selectively utilize image, question and answer information, we propose a novel trilinear interaction model which simultaneously learns high level associations between these three inputs. In addition, to overcome the interaction complexity, we introduce a multimodal tensor-based PARALIND decomposition which effificiently parameterizes trilinear interaction between the three inputs. Moreover, knowledge distillation is fifirst time applied in Free-form Opened-ended VQA. It is not only for reducing the computational cost and required memory but also for transferring knowledge from trilinear interaction model to bilinear interaction model. The extensive experiments on benchmarking datasets TDIUC, VQA-2.0, and Visual7W show that the proposed compact trilinear interaction model achieves state-of-the-art results when using a single model on all three datasets.
作者认为在视觉问题解答(VQA)中,答案与问题含义和视觉内容有很大的关联。 因此,为了有选择地利用图像,问题和答案信息,我们提出了一种新颖的三线性交互模型,该模型同时学习了这三个输入之间的高级关联。 此外,为了克服交互的复杂性,我们引入了基于多模态张量的PARALIND分解,该分解有效地参数化了三个输入之间的三线性交互。 此外,知识蒸馏是首次应用于自由形式的开放式VQA。 它不仅用于减少计算成本和所需的内存,还用于将知识从三线性交互模型转移到双线性交互模型。
二、网络框架介绍
令![]() 代表三个输入的表示。
代表三个输入的表示。 ![]() ,其中
,其中![]() 是输入
是输入![]() 的通道数,而
的通道数,而![]() 是每个通道的维度。例如,如果
是每个通道的维度。例如,如果![]() 是图像的基于区域的表示,则
是图像的基于区域的表示,则![]() 是区域的数量,而
是区域的数量,而![]() 是每个区域的特征表示的尺寸。令
是每个区域的特征表示的尺寸。令![]() 是
是![]() 的第
的第 ![]() 行,即
行,即![]() 中第
中第 ![]() 个通道的特征表示,其中
个通道的特征表示,其中![]() ,作者提出的模型应用到了视觉问答的多项选择和自由问答题目,下面进行详细的分析。
,作者提出的模型应用到了视觉问答的多项选择和自由问答题目,下面进行详细的分析。
2.1. Fully parameterized trilinear interaction
由三个输入上的完全参数化的三线性相互作用产生的联合表示由![]() 表示,其计算如下
表示,其计算如下
其中,![]() 是一个学习张量;
是一个学习张量;![]()
![]() 是
是![]() 的向量化,输出行向量;运算符
的向量化,输出行向量;运算符![]() 表示
表示![]() 张量积。
张量积。
张量![]() 有助于通过
有助于通过![]() 张量积学习三个输入之间的相互作用。但是,当每个输入模态的维数
张量积学习三个输入之间的相互作用。但是,当每个输入模态的维数![]() 高时,学习如此大的张量
高时,学习如此大的张量![]() 是不可行的,这是VQA中的常见情况。因此,有必要减小
是不可行的,这是VQA中的常见情况。因此,有必要减小![]() 的大小,使学习变得可行。
的大小,使学习变得可行。
在[Zichao Yang等人]的启发下,我们依靠单一注意机制的思想。具体而言,令![]() 为通道的第
为通道的第![]() 个三元组的联合表示,其中三元组中的每个通道都来自不同的输入。三元组中每个通道的表示分别为
个三元组的联合表示,其中三元组中的每个通道都来自不同的输入。三元组中每个通道的表示分别为![]() ,其中
,其中![]() 。三个输入上有
。三个输入上有![]() 个可能的三元组。由第
个可能的三元组。由第![]() 个三元组的三个通道表示
个三元组的三个通道表示![]() 上的完全参数化的三线性相互作用得出的联合表示
上的完全参数化的三线性相互作用得出的联合表示![]() 计算如下
计算如下
其中![]() 是三元组中通道之间的学习张量。
是三元组中通道之间的学习张量。
遵循统一注意力[Zichao Yang等人]的想法,通过使用(2)中描述的所有三元组的联合表示来近似联合表示 ![]() ,而不是像(1)那样在三个输入上使用完全参数化的交互。 因此,我们计算
,而不是像(1)那样在三个输入上使用完全参数化的交互。 因此,我们计算
请注意,在(3)中,我们计算所有可能的三元组的加权和。 第![]() 个三元组与标量权重
个三元组与标量权重![]() 相关联。
相关联。![]() 的集合称为注意力图
的集合称为注意力图![]() ,其中
,其中![]() 。
。
通过减少三个输入![]() 和
和![]() 上的参数化三线性相互作用产生的注意力图
上的参数化三线性相互作用产生的注意力图![]() 的计算如下
的计算如下
其中,![]() 是注意力图
是注意力图![]() 的学习张量。注意,与(1)中的学习张量
的学习张量。注意,与(1)中的学习张量![]() 相比,(4)中的学习张量
相比,(4)中的学习张量![]() 的大小减小。
的大小减小。
通过将(2)集成到(3)中,可以将(3)中的联合表示 ![]() 重写为
重写为
其中(5)中的![]() 实际上是(4)中注意图
实际上是(4)中注意图![]() 的标量注意权重
的标量注意权重![]() 。
。
从(5)还值得注意的是,计算 ![]() 不是学习(1)中的大张量
不是学习(1)中的大张量![]() ,而我们现在只需要学习(2)中的
,而我们现在只需要学习(2)中的![]() 和(4)中
和(4)中![]() 的两个较小的张量。
的两个较小的张量。
2.2. Parameter factorization
尽管三线性相互作用模型的大张量![]() 被两个较小的张量
被两个较小的张量![]() 和
和![]() 代替,但这两个张量的维数仍然很大,这使学习变得困难。为了进一步降低计算复杂度,将PARALIND分解应用于
代替,但这两个张量的维数仍然很大,这使学习变得困难。为了进一步降低计算复杂度,将PARALIND分解应用于![]() 和
和![]() 。 学习张量
。 学习张量![]() 的PARALIND分解可计算为
的PARALIND分解可计算为
其中![]() 是切片参数,在分解速率(与使用内存和计算成本直接相关)与性能之间进行权衡。每个
是切片参数,在分解速率(与使用内存和计算成本直接相关)与性能之间进行权衡。每个![]() 是一个较小的可学习张量,称为Tucker张量。 这些Tucker张量的数量等于
是一个较小的可学习张量,称为Tucker张量。 这些Tucker张量的数量等于![]() 。
。![]() 的最大值通常设置为
的最大值通常设置为![]() 和
和![]() 的最大公约数。 在我们的实验中,我们发现R = 32给出了分解速率和性能之间的良好折衷。
的最大公约数。 在我们的实验中,我们发现R = 32给出了分解速率和性能之间的良好折衷。
在这里,我们的维度为![]() ,
,![]() 和
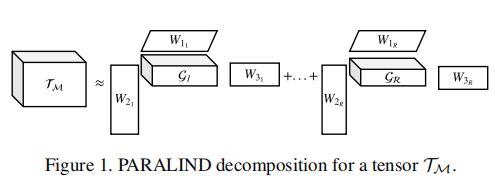
和![]() 是可学习的因子矩阵。图1显示了张量
是可学习的因子矩阵。图1显示了张量![]() 的PARALIND分解图。
的PARALIND分解图。
(6)中![]() 的缩写形式可以重写为
的缩写形式可以重写为
将学习张量![]() 从(7)集成到(4)中,注意力图
从(7)集成到(4)中,注意力图![]() 可以重写为
可以重写为
与![]() 相似,也将PARALIND分解应用于(5)中的张量
相似,也将PARALIND分解应用于(5)中的张量![]() 以降低复杂度。值得注意的是,
以降低复杂度。值得注意的是,![]() 的大小直接影响联合表示
的大小直接影响联合表示![]() 的大小。因此,为了使信息损失最小化,我们将切片参数R = 1设置为因子矩阵的投影维数为
的大小。因此,为了使信息损失最小化,我们将切片参数R = 1设置为因子矩阵的投影维数为 ![]() ,即联合表示
,即联合表示 ![]() 的维数相同。
的维数相同。
因此,(5)中的![]() 可计算为
可计算为
其中![]() 是可学习因子矩阵,而
是可学习因子矩阵,而![]() 是较小的张量(与
是较小的张量(与![]() 相比)。
相比)。
到目前为止,我们已经有![]() (8)和
(8)和![]() (9),因此,我们可以使用(5)计算
(9),因此,我们可以使用(5)计算 ![]() 。 可以将(5)中的
。 可以将(5)中的 ![]() 重写为
重写为
在此,有趣的是,(10)中的![]() 具有秩为1。因此,从(10)中的i-mode张量积得到的结果可以用Hadamard积近似,而没有秩为1的张量
具有秩为1。因此,从(10)中的i-mode张量积得到的结果可以用Hadamard积近似,而没有秩为1的张量![]() 。特别是,可以不使用
。特别是,可以不使用![]() 来计算(10)中的
来计算(10)中的 ![]() 。
。
请注意,作为联合嵌入维度的 ![]() 是用户定义的参数,它在表示能力和计算成本之间进行了权衡。在作者的实验中,我们发现
是用户定义的参数,它在表示能力和计算成本之间进行了权衡。在作者的实验中,我们发现 ![]() = 1,024可以取得很好的折衷。
= 1,024可以取得很好的折衷。
2.3. Compact Trilinear Interaction for VQA
训练![]() 的输入是
的输入是![]() 的集合,其中
的集合,其中![]() 是图像表示;
是图像表示; ![]() ,其中
,其中 ![]() 是图像中感兴趣区域(或边界框)的数量,而
是图像中感兴趣区域(或边界框)的数量,而 ![]() 是区域表示的维度;
是区域表示的维度;![]() 是问题的表示;
是问题的表示; ![]() ,其中,
,其中,![]() 是隐藏状态的数量,
是隐藏状态的数量, ![]() 是每个隐藏状态的维度。
是每个隐藏状态的维度。![]() 是答案表示;
是答案表示; ![]() ,其中
,其中 ![]() 是隐藏状态的数量,
是隐藏状态的数量,![]() 是每个隐藏状态的维度。
是每个隐藏状态的维度。
通过将紧凑三线性相互作用(CTI)应用于每个![]() ,我们获得联合表示
,我们获得联合表示![]() 。 具体来说,我们首先通过(8)式计算注意力图
。 具体来说,我们首先通过(8)式计算注意力图![]()
![]()
然后,由(11)计算联合表示 ![]()
其中,(12)中的![]() 和(13)中的
和(13)中的![]() 是可学习的因子矩阵; (12)中的每个
是可学习的因子矩阵; (12)中的每个![]() 是可学习的Tucker张量。
是可学习的Tucker张量。
2.3.1Multiple Choice Visual Question Answering
为了与MC VQA 中的最新技术进行公平比较,我们遵循这些作品中使用的表示法。具体来说,每个输入问题和每个答案的最大长度为12个单词,如果少于12个单词,则将其补零。然后,每个单词用一个300-D的GloVe单词嵌入来表示。每个图像都由一个14×14×2048网格特征(即196个单元;每个单元具有2,048-D特征)表示,该图像是从ImageNet上经过预训练的ResNet-152的第二倒数第二层中提取的。
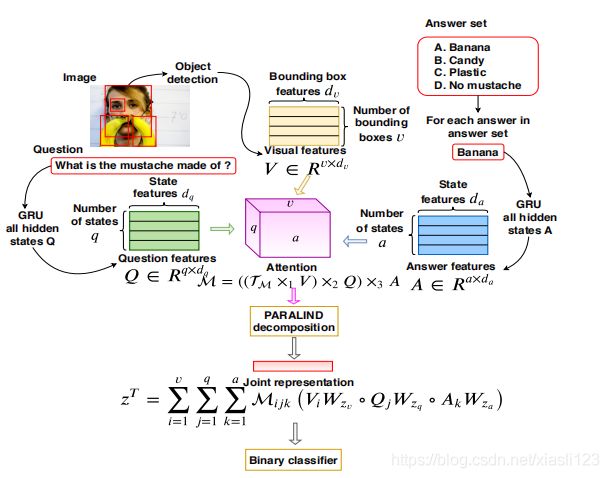
按照[41],输入样本分为正样本和负样本。一个正样本在二进制分类中被标记为1,其中包含图像,问题和正确答案。 负样本(在二进制分类中标记为0)包含图像,问题和错误答案。然后将这些样本传递给我们提出的CTI,以获得联合表示 ![]() 。联合表示通过二进制分类器来获得预测。二进制交叉熵损失用于训练所提出的模型。 图2可视化了将CTI应用于MC VQA时,所提出的模型。
。联合表示通过二进制分类器来获得预测。二进制交叉熵损失用于训练所提出的模型。 图2可视化了将CTI应用于MC VQA时,所提出的模型。
![]()
2.3.2. Free-Form Opened-Ended Visual Question Answering
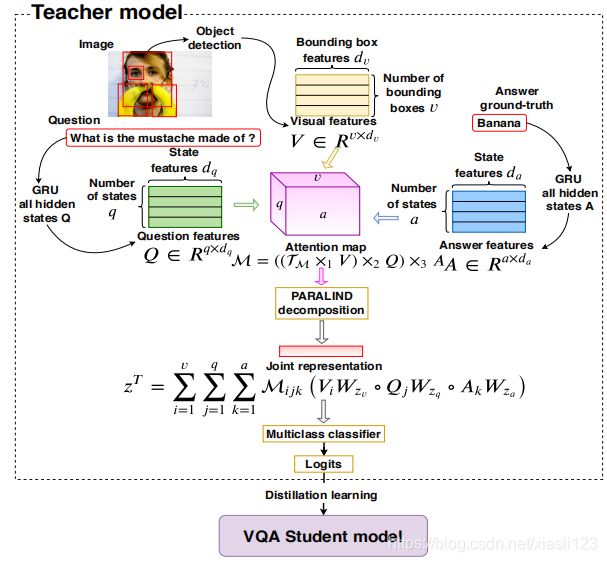
与MC VQA不同,FFOE VQA将答案视为预定义答案集上的分类问题。因此,每个问题-图像对的集合设置可能的答案比MC VQA的情况要多得多。因此,在2.3.1节中提出的模型设计,即对于每个问题-图像输入,该模型从其答案列表中获取所有可能的答案以计算联合表示,从而导致较高的计算成本。此外,提出的的CTI模型需要所有三个V,Q,A输入来计算联合表示。然而,在测试期间,FFOE VQA中没有可用的答案信息。为了克服这些挑战,作者提出使用知识蒸馏将学习到的知识从教师模型转移到学生模型。 图3可视化了FFOE VQA的模型设计。
![]()
我们的教师模型将三元组的图像-问题-正确答案作为输入。每个三元组都通过提出的CTI模型来获得联合表示 ![]() 。然后将联合表示
。然后将联合表示 ![]() 传递给多类分类器(在预定义答案的集合上)以获得预测,交叉熵损失用于训练教师模型。关于学生模型,任何最先进的VQA都可以使用,在作者的实验中,我们使用BAN2或SAN作为学生模型。学生模型将成对的图像-问题作为输入,并将预测视为多类分类问题。 学生模型的损失函数定义为
传递给多类分类器(在预定义答案的集合上)以获得预测,交叉熵损失用于训练教师模型。关于学生模型,任何最先进的VQA都可以使用,在作者的实验中,我们使用BAN2或SAN作为学生模型。学生模型将成对的图像-问题作为输入,并将预测视为多类分类问题。 学生模型的损失函数定义为
其中![]() 代表交叉熵损失;
代表交叉熵损失; ![]() 是学生的标准
是学生的标准 ![]() 输出;
输出;![]() 是真实答案标签;α是用于控制每个损失成分的重要性的超参数;
是真实答案标签;α是用于控制每个损失成分的重要性的超参数;![]() 是软化的输出,其计算如下
是软化的输出,其计算如下
其中对于老师和学生模型, ![]() 是相应分类器输出的预测。
是相应分类器输出的预测。
遵循FFOE VQA的最新技术,对于图像表示,我们使用FPN检测器(ResNet152主干)使用基于对象检测的功能,其中最大检测到的边界框的数量设置为50 。对于问题和答案表示,我们将问题和答案最多裁剪为12个单词,如果少于12个单词,则将其补零。 然后,每个词都由600-D向量表示,该向量是300-D GloVe词嵌入和来自训练数据的扩充嵌入的串联。换句话说,问题的表示维度为12×600,答案与之相似。
三、实验分析
实验是在具有12GB RAM的NVIDIA Titan V GPU上进行的。在所有实验中,学习率均设置为![]() 。批量大小设置为128(用于训练MC VQA)和256大小用于FFOE VQA。 当训练MC VQA模型和FFOE VQA模型时,除了图像表示提取之外,其他组件也用端到端训练。 (15)中的参数T设置为3。MC VQA和FFOE VQA的联合表示
。批量大小设置为128(用于训练MC VQA)和256大小用于FFOE VQA。 当训练MC VQA模型和FFOE VQA模型时,除了图像表示提取之外,其他组件也用端到端训练。 (15)中的参数T设置为3。MC VQA和FFOE VQA的联合表示 ![]() 的维度都设置为1,024。
的维度都设置为1,024。
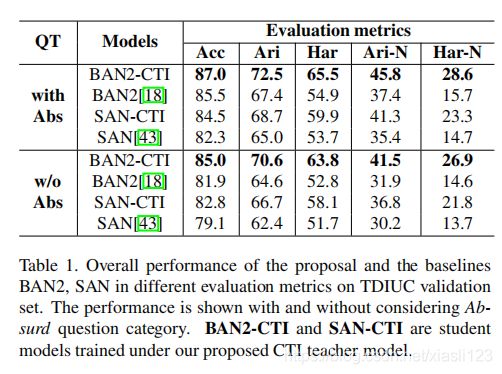
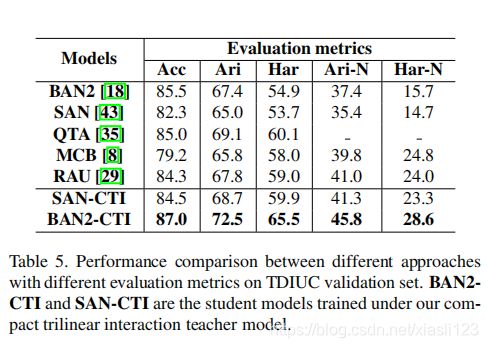
表1给出了对TDIUC五个不同指标的综合评估。
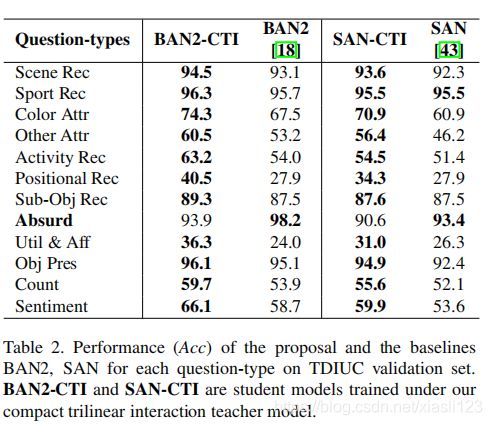
表2列出了当所有类别(包括“Absurd”)都用于培训时,在TDIUC的每个问题类别上使用Acc度量的详细表现。
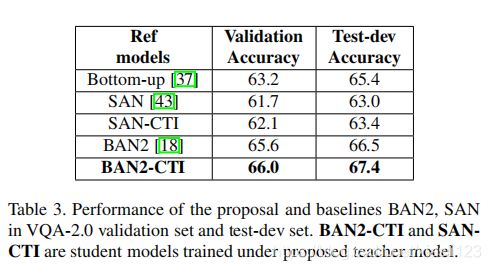
表3列出了我们的蒸馏学生模型与两个基准BAN2,SAN在VQA-2.0上的Acc度量标准之间的比较结果。
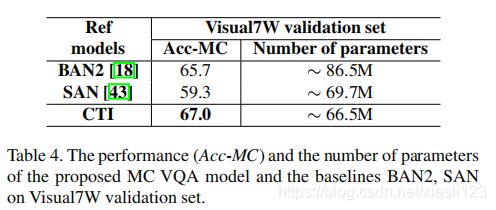
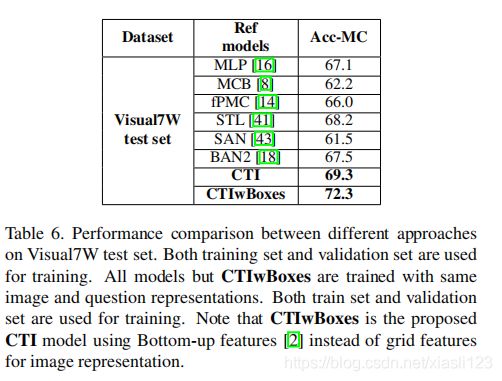
表4给出了Visual7W与Acc-MC度量的比较结果。
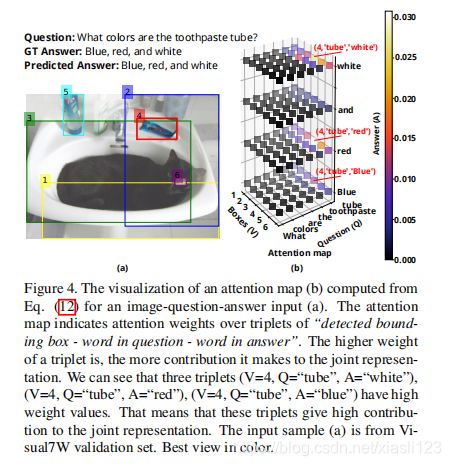
图4将CTI产生的注意力图可视化为一个图像问题答案示例。
表5显示,我们蒸馏的学生BAN2-CTI在所有度量指标上的优于所有比较方法。
关于MCVQA,表6显示,所提出的模型(表6中表示为CTI)的性能明显优于比较方法。
四、结论
We propose a novel compact trilinear interaction which simultaneously learns high level associations between image, question, and answer in both MC VQA and FFOE VQA. In addition, knowledge distillation is the first time applied to FFOE VQA to overcome the computational complexity and memory issue of the interaction. The extensive experimental results show that the proposed models achieve the state-of-the-art results on three benchmarking datasets.
为了使用(1)在三个输入之间进行完全交互,需要学习21990.2亿个参数,这在实践中是不可行的。 通过使用PARALIND分解以及提供的设置,即切片数R = 32和联合表示的维数![]() = 1024,需要学习的参数数仅为3369万。 换句话说,这样达到了约65,280的分解率。
= 1024,需要学习的参数数仅为3369万。 换句话说,这样达到了约65,280的分解率。
本论文也是利用张量来学习多模态的交互性,与前两篇论文不同的是加入了答案作为交互,使用了PARALIND分解,另外还引入了前所未有的知识蒸馏进行学习。尽管效果还不是太好,但是这样的思想方法还是值得借鉴的。