第六周【任务2】卷积神经网络:前向后向传播(笔记)
CNN 前向后向算法
单通道二维图像示例
CNN的一个难点就是在具体计算过程中实现前向后向传播算法。因为CNN的卷积核是方阵,不方便在具体矩阵运算中运行。因此对于具体的运行,我们要做一点变化。假设我们有 5 × 4 × 1 5\times 4\times 1 5×4×1输入图像 x \boldsymbol{x} x和卷积核 W W W, b b b. 同时stride=1, padding=0. 我们有
x 11 x 12 x 13 x 14 x 21 x 22 x 23 x 24 x 31 x 32 x 33 x 34 x 41 x 42 x 43 x 44 x 51 x 52 x 53 x 54 x 61 x 62 x 63 x 64 ∗ w 11 w 12 w 21 w 22 = y 11 y 12 y 13 y 21 y 22 y 23 y 31 y 32 y 33 y 41 y 42 y 43 y 51 y 52 y 53 \begin{array}{|c|c|c|c|} \hline x_{11} & x_{12} & x_{13} & x_{14} \\ \hline x_{21} & x_{22} & x_{23} & x_{24} \\ \hline x_{31} & x_{32} & x_{33} & x_{34} \\ \hline x_{41} & x_{42} & x_{43} & x_{44} \\ \hline x_{51} & x_{52} & x_{53} & x_{54} \\ \hline x_{61} & x_{62} & x_{63} & x_{64} \\ \hline \end{array} * \begin{array}{|l|l|} \hline w_{11} & w_{12} \\ \hline w_{21} & w_{22} \\ \hline \end{array} = \begin{array}{|l|l|l|} \hline y_{11} & y_{12} & y_{13} \\ \hline y_{21} & y_{22} & y_{23} \\ \hline y_{31} & y_{32} & y_{33} \\ \hline y_{41} & y_{42} & y_{43} \\ \hline y_{51} & y_{52} & y_{53} \\ \hline \end{array} x11x21x31x41x51x61x12x22x32x42x52x62x13x23x33x43x53x63x14x24x34x44x54x64∗w11w21w12w22=y11y21y31y41y51y12y22y32y42y52y13y23y33y43y53
我们可以做变形
x 11 x 12 x 21 x 22 x 12 x 13 x 22 x 23 x 13 x 14 x 23 x 24 x 21 x 22 x 31 x 32 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ x 53 x 54 x 63 x 64 ∗ w 11 w 12 w 21 w 22 = y 11 y 12 y 13 y 21 ⋮ y 53 \begin{array}{|l|l|l|l|} \hline x_{11} & x_{12} & x_{21} & x_{22} \\ \hline x_{12} & x_{13} & x_{22} & x_{23} \\ \hline x_{13} & x_{14} & x_{23} & x_{24} \\ \hline x_{21} & x_{22} & x_{31} & x_{32} \\ \hline & & & \\ \hline \vdots & \vdots & \vdots & \vdots \\ \vdots & \vdots & \vdots & \vdots \\ \hline x_{53} & x_{54} & x_{63} & x_{64} \\ \hline \end{array} * \begin{array}{|l|} \hline w_{11} \\ \hline w_{12} \\ \hline w_{21} \\ \hline w_{22} \\ \hline \end{array} = \begin{array}{|l|} \hline y_{11} \\ \hline y_{12} \\ \hline y_{13} \\ \hline y_{21} \\ \hline \\ \vdots \\ \hline y_{53} \\ \hline \end{array} x11x12x13x21⋮⋮x53x12x13x14x22⋮⋮x54x21x22x23x31⋮⋮x63x22x23x24x32⋮⋮x64∗w11w12w21w22=y11y12y13y21⋮y53
具体来说,我们首先把卷积核转变为一个一维向量。这样就使得我们必须重新排序输入图像的元素。因为在卷积核遍历图像角落的过程中,不同元素可能与输入图像中的同一个元素相乘。 比如元素 x 12 x_{12} x12。 这样的结果也就使得输出的矩阵 y \boldsymbol{y} y也必须要重新转变为一个一维向量。
我们重新标记重新排序后的输入图像和输出为 x ~ , W ~ , y ~ \tilde{\boldsymbol{x}}, \tilde{W}, \tilde{\boldsymbol{y}} x~,W~,y~. 因此有
y ~ = x ~ ⋅ w ~ ∂ J ∂ w ~ = x ~ T ∂ J ∂ y ~ ∂ J ∂ b ~ = sumRow ∂ J ∂ y ~ ∂ J ∂ x ~ = ∂ J ∂ y ~ w ~ T ∂ J ∂ x i j = ∑ ∂ J ∂ x i ′ j ′ ~ \tilde{y}=\tilde{x} \cdot \widetilde{w}\\ \frac{\partial J}{\partial \widetilde{w}}=\tilde{x}^{T} \frac{\partial J}{\partial \tilde{y}}\\ \frac{\partial J}{\partial \tilde{b}}=\operatorname{sumRow} \frac{\partial J}{\partial \tilde{y}}\\ \frac{\partial J}{\partial \tilde{x}}=\frac{\partial J}{\partial \tilde{y}} \widetilde{w}^{T}\\ \frac{\partial J}{\partial x_{i j}}=\sum \frac{\partial J}{\partial \widetilde{x_{i^{\prime} j^{\prime}}}} y~=x~⋅w ∂w ∂J=x~T∂y~∂J∂b~∂J=sumRow∂y~∂J∂x~∂J=∂y~∂Jw T∂xij∂J=∑∂xi′j′ ∂J
【矩阵求导顺序?】
这里要注意,因为我们原来做的卷积核运算中,在卷积核遍历图像角落的过程中,不同元素可能与输入图像中的同一个元素相乘。在 x → x ~ x\rightarrow \tilde{x} x→x~时,我们要保存原来的索引,这样我们才可以在对 x ~ i j \tilde{x}_{ij} x~ij求导后,再通过原来的索引进行相加 ∂ J ∂ x i j = ∑ ∂ J ∂ x i j ~ \frac{\partial J}{\partial x_{i j}}=\sum \frac{\partial J}{\partial \widetilde{x_{i j}}} ∂xij∂J=∑∂xij ∂J.这里为什么要做加和呢?因为stride=1, 卷积核在遍历的时候,对某些元素,比如 x 12 x_{12} x12,进行了多次操作,
y 11 = x 11 w 11 + x 12 w 12 + x 21 w 21 + x 22 w 22 y 12 = x 12 w 11 + x 13 w 12 + x 22 w 21 + x 23 w 22 y_{11}=x_{11}w_{11} + x_{12}w_{12} + x_{21}w_{21} + x_{22}w_{22}\\ y_{12}=x_{12}w_{11} + x_{13}w_{12} + x_{22}w_{21} + x_{23}w_{22} y11=x11w11+x12w12+x21w21+x22w22y12=x12w11+x13w12+x22w21+x23w22
所以对于 ∂ J ∂ x 12 \dfrac{\partial J}{\partial x_{12}} ∂x12∂J, 应该有 ∂ J ∂ x 12 = ∂ J ∂ y 11 ⋅ ∂ y 11 ∂ x 12 + ∂ J ∂ y 12 ⋅ ∂ y 12 ∂ x 12 = ∂ J ∂ y 11 w 12 + ∂ J ∂ y 12 w 11 \dfrac{\partial J}{\partial x_{12}}=\dfrac{\partial J}{\partial y_{11}}\cdot \dfrac{\partial y_{11}}{\partial x_{12}} + \dfrac{\partial J}{\partial y_{12}}\cdot \dfrac{\partial y_{12}}{\partial x_{12}}=\dfrac{\partial J}{\partial y_{11}}w_{12} + \dfrac{\partial J}{\partial y_{12}}w_{11} ∂x12∂J=∂y11∂J⋅∂x12∂y11+∂y12∂J⋅∂x12∂y12=∂y11∂Jw12+∂y12∂Jw11. 因此我们应该在 x ~ \widetilde{x} x 找到所有的等于 x 12 x_{12} x12的元素所在索引位置,分别进行 ∂ J ∂ y ~ w \dfrac{\partial J}{\partial \tilde{y}}w ∂y~∂Jw求导操作,然后把所有这些操作得到的值加起来。
【 ∂ J ∂ x i j = ∑ ∂ J ∂ x i ′ , j ′ ~ \frac{\partial J}{\partial x_{i j}}=\sum \frac{\partial J}{\partial \widetilde{x_{i^{\prime}, j^{\prime}}}} ∂xij∂J=∑∂xi′,j′ ∂J中的求和,不是针对i, j求和,而是找到所有等于 x i , j x_{i, j} xi,j的 x i ′ , j ′ ~ \widetilde{x_{i^{\prime}, j^{\prime}}} xi′,j′ 的位置,然后各个位置上求导出结果,然后再求和】
如果有N个样本做一个batch训练,我们就把不同的样本转化后的 x ~ \widetilde{x} x 拼接起来,再做如上操作。
多通道二维图像示例
假设现在一个样本是3通道的二维图像,卷积核有两个。那么我们针对一个通道有
Y 11 Y 12 Y 13 Y 14 Y 21 Y 22 Y 23 Y 24 ∗ w 11 1 w 12 1 w 21 1 w 22 1 + g 11 g 12 g 13 g 14 g 21 g 22 g 23 g 24 ∗ w 11 2 w 12 2 w 21 2 w 22 2 + b 11 b 12 b 13 b 14 b 21 b 22 b 23 b 24 ∗ w 11 3 w 12 3 w 21 3 w 22 3 = y 11 1 y 12 1 y 13 1 \begin{array}{|l|l|l|l|} \hline Y_{11} & Y_{12} &Y_{13} &Y_{14} \\ \hline Y_{21} & Y_{22} &Y_{23} &Y_{24} \\ \hline & & & \\ \hline & & & \\ \hline & & & \\ \hline & & & \\ \hline \end{array} * \begin{array}{|c|c|} \hline w_{11}^{1} & w_{12}^{1} \\ \hline w_{21}^{1} & w_{22}^{1} \\ \hline \end{array} + \\ \begin{array}{|l|l|l|l|} \hline g_{11} & g_{12} &g_{13} &g_{14} \\ \hline g_{21} & g_{22} &g_{23} &g_{24} \\ \hline & & & \\ \hline & & & \\ \hline & & & \\ \hline & & & \\ \hline \end{array}*\begin{array}{|c|c|} \hline w_{11}^{2} & w_{12}^{2} \\ \hline w_{21}^{2} & w_{22}^{2} \\ \hline \end{array} +\\ \begin{array}{|l|l|l|l|} \hline b_{11} & b_{12} &b_{13} &b_{14} \\ \hline b_{21} & b_{22} &b_{23} &b_{24} \\ \hline & & & \\ \hline & & & \\ \hline & & & \\ \hline & & & \\ \hline \end{array}*\begin{array}{|c|c|} \hline w_{11}^{3} & w_{12}^{3} \\ \hline w_{21}^{3} & w_{22}^{3} \\ \hline \end{array} =\begin{array}{|c|c|c|} \hline y_{11}^{1} & y_{12}^{1} & y_{13}^{1} \\ \hline & & \\ \hline & & \\ \hline & & \\ \hline & & \\ \hline \end{array}\\ Y11Y21Y12Y22Y13Y23Y14Y24∗w111w211w121w221+g11g21g12g22g13g23g14g24∗w112w212w122w222+b11b21b12b22b13b23b14b24∗w113w213w123w223=y111y121y131
对于整体我们有
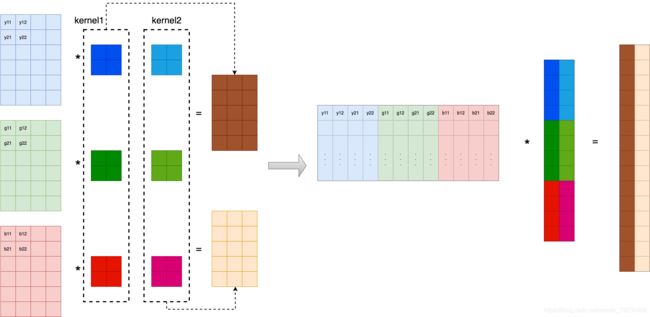
同样可以写成式子
y ~ = x ~ ⋅ w ~ ∂ J ∂ w ~ = x ~ T ∂ J ∂ y ~ ∂ J ∂ b ~ = SumRow ( ∂ J ∂ y ~ ) ∂ J ∂ x ~ = ∂ J ∂ y ~ w ~ T \begin{array}{l} \tilde{y}=\tilde{x} \cdot \widetilde{w} \\ \dfrac{\partial J}{\partial \widetilde{w}}=\tilde{x}^{T} \dfrac{\partial J}{\partial \tilde{y}} \\ \dfrac{\partial J}{\partial \tilde{b}}=\operatorname{SumRow}\left(\dfrac{\partial J}{\partial \tilde{y}}\right)\\ \dfrac{\partial J}{\partial \tilde{x}}=\dfrac{\partial J}{\partial \tilde{y}} \widetilde{w}^{T} \end{array} y~=x~⋅w ∂w ∂J=x~T∂y~∂J∂b~∂J=SumRow(∂y~∂J)∂x~∂J=∂y~∂Jw T
池化层的前向后向
平均池化
平均池化的情况可以等价于卷积层参数都是 1 / k 1/k 1/k, 比如
y 11 = 1 4 ( x 11 + x 12 + x 21 + x 22 ) ⇒ ∂ J ∂ x 11 = ∂ J ∂ y 11 ⋅ 1 4 , ∂ J ∂ x 12 = ∂ J ∂ y 11 ⋅ 1 4 , ⋯ y_{11}=\frac{1}{4}\left(x_{11}+x_{12}+x_{21}+x_{22}\right) \\ \Rightarrow \frac{\partial J}{\partial x_{11}}=\frac{\partial J}{\partial y_{11}} \cdot \frac{1}{4}, \frac{\partial J}{\partial x_{12}}=\frac{\partial J}{\partial y_{11}} \cdot \frac{1}{4}, \cdots y11=41(x11+x12+x21+x22)⇒∂x11∂J=∂y11∂J⋅41,∂x12∂J=∂y11∂J⋅41,⋯
因此可以转化为 w i j = 1 4 w_{ij}=\frac{1}{4} wij=41的卷积
x 11 x 12 x 21 x 22 x 12 x 13 x 22 x 23 ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ∗ 1 4 1 4 1 4 = y 11 y 12 y 13 ⋅ ⋅ \begin{array}{|c|c|c|c|} \hline x_{11} & x_{12} & x_{21} & x_{22} \\ \hline x_{12} & x_{13} & x_{22} & x_{23} \\ \hline \cdot & \cdot & & \\ \cdot & \cdot & & \\ \cdot & \cdot & & \\ \hline \end{array} * \begin{array}{|c|} \hline \frac{1}{4} \\ \hline \frac{1}{4} \\ \hline \frac{1}{4} \\ \hline \end{array}= \begin{array}{|l|} \hline y_{11} \\ \hline y_{12} \\ \hline y_{13} \\ \hline \cdot\\ \hline \cdot\\ \hline \end{array} x11x12⋅⋅⋅x12x13⋅⋅⋅x21x22x22x23∗414141=y11y12y13⋅⋅
求导同样可以采用
∂ J ∂ x ~ = ∂ J ∂ y ~ w ~ T \frac{\partial J}{\partial \tilde{x}}=\frac{\partial J}{\partial \tilde{y}} \widetilde{w}^{T} ∂x~∂J=∂y~∂Jw T
最大池化
对于max pooling, 我们有
y 11 = max ( x 11 , x 12 , x 21 , x 22 ) y 12 = max ( x 12 , x 13 , x 22 , x 23 ) \begin{array}{l} y_{11}=\max \left(x_{11}, x_{12}, x_{21}, x_{22}\right) \\ y_{12}=\max \left(x_{12}, x_{13}, x_{22}, x_{23}\right) \end{array} y11=max(x11,x12,x21,x22)y12=max(x12,x13,x22,x23)
如果求导,就有
∂ J ∂ x 11 = ∂ J ∂ y 11 d y 11 d x 11 = ∂ J ∂ y 11 = { 1 , i f x 11 i s t h e m a x 0 , e l s e \frac{\partial J}{\partial x_{11}}=\frac{\partial J}{\partial y_{11}} \frac{\mathrm{d} y_{11}}{\mathrm{~d} x_{11}}=\frac{\partial J}{\partial y_{11}}= \left\{\begin{array}{l} 1, if\ x_{11}\ is\ the\ max\\ 0, else \end{array}\right. ∂x11∂J=∂y11∂J dx11dy11=∂y11∂J={ 1,if x11 is the max0,else
这里的情况就比较tricky,因为我们即使把权重w看做1,这里的1在每一行的分布也是不一样的。对于求 ∂ J ∂ x ~ = ∂ J ∂ y ~ d y ~ d x ~ \dfrac{\partial J}{\partial \tilde{x}}=\dfrac{\partial J}{\partial \tilde{y}} \dfrac{\mathrm{d} \tilde{y}}{\mathrm{~d} \tilde{x}} ∂x~∂J=∂y~∂J dx~dy~, 我们首先要遍历 ∂ J ∂ x ~ \dfrac{\partial J}{\partial \tilde{x}} ∂x~∂J的每一行,找出此行在原来 x ~ \tilde{x} x~对应行的最大值的列索引。比如 ∂ J ∂ x ~ \dfrac{\partial J}{\partial \tilde{x}} ∂x~∂J第一行有四个元素,假设对应的 x ~ \tilde{x} x~的四个元素中的最大值是 x 21 x_{21} x21, 列索引就是3, 那么 ∂ J ∂ x ~ \dfrac{\partial J}{\partial \tilde{x}} ∂x~∂J第一行就变为 [ 0 , 0 , ∂ J ∂ y 11 , 0 ] [0, 0, \dfrac{\partial J}{\partial y_{11}}, 0] [0,0,∂y11∂J,0]. 也就是说第一行除了第三列,其余列的值均设为0。