LeetCode 96不同的二叉搜索树&95不同的二叉搜索树Ⅱ
微信搜一搜:
bigsai
算法文章题解全部收录在github仓库bigsai-algorithm
关注回复进群即可加入力扣打卡群,欢迎划水。近期打卡:
LeetCode 92反转链表Ⅱ&93复制ip地址&94二叉树的中序遍历
LeetCode 90子集Ⅱ&91解码方法
LeetCode 88合并两个有序数组&89格雷编码
96 不同的二叉搜索树Ⅱ
给定一个整数 n,求以 1 … n 为节点组成的二叉搜索树有多少种?
示例:
输入: 3
输出: 5
解释:
给定 n = 3, 一共有 5 种不同结构的二叉搜索树:
1 3 3 2 1
\ / / / \ \
3 2 1 1 3 2
/ / \ \
2 1 2 3
分析
首先弄清这棵树是一颗二叉搜索树。大的节点只能在右侧,小的在左侧。所以n个节点如果以第i为节点,那么[1-i-1]的都在左侧,[i+1,n]都在右侧。
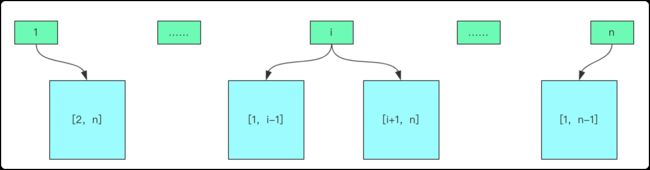
如果单单从结构上考虑那么就是:
左侧0个数量 x 右侧n-1个数量
左侧1个数量 x 右侧n-2个数量
左侧2个数量 x 右侧n-3个数量
……
左侧n-1个数量 x 右侧0个数量
所以这个题父子关系很大,从上就能得到这样的递推,当然这题我们使用动态规划来解决,dp[i]表示i个节点所有可以排列的数量。就得到状态转移方程:
dp[i]=sum(dp[j]*dp[i-j-1]) j∈[0,i)(左右子节点之和为i-1)
实现代码为:
class Solution {
public int numTrees(int n) {
if(n<2)return n;
int dp[]=new int [n+1];
dp[0]=1;
dp[1]=1;
for(int i=2;i<n+1;i++)
{
for(int j=0;j<i;j++)
{
dp[i]+=dp[j]*dp[i-j-1];
}
}
return dp[n];
}
}
95不同的二叉搜索树Ⅱ
给定一个整数 n,生成所有由 1 … n 为节点所组成的 二叉搜索树 。
示例:
输入:3
输出:
[
[1,null,3,2],
[3,2,null,1],
[3,1,null,null,2],
[2,1,3],
[1,null,2,null,3]
]
解释:
以上的输出对应以下 5 种不同结构的二叉搜索树:
1 3 3 2 1
\ / / / \ \
3 2 1 1 3 2
/ / \ \
2 1 2 3
提示:
0 <= n <= 8
分析
这题和上一题不一样,要求我们返回所有可能的这么一个树,这题的话我还是使用递归的方式,当然不可以无脑递归然后去构造这棵树因为可能会有重复比如 2 3 1 和 2 1 3这个序列构成树的结果是一致的。
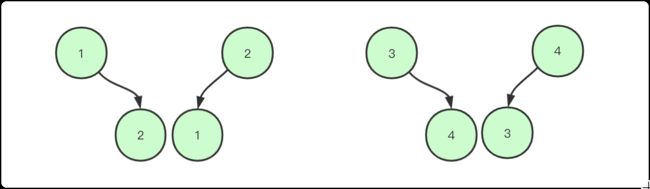
所以要考虑一个没有重复但能全部覆盖的策略。这题和上一题有一些不一样的地方就是上一题通过dp可能很多连续数不同但是结构相同我们可以不计算,但这里面每一种情况都需要构建。
所以这题怎么考虑呢?和上题一样,对于n个节点,我们需要考虑的其实就是n个节点每个为根节点的构造可能性。单独考虑第i个节点,第i个节点的left和right分别对应一个节点。所以要找到这种节点组合的排列可能。
在具体实现上我们借助一个递归函数generateTrees(int start, int end)表示从start到end的所有满足条件的节点。而在这个递归调用的过程中,我们循环递归分别获取根为第1,2,3……n个节点的组成情况(递归调用获取左右部分节点然后新建节点左右部分)。
具体代码为:
public List<TreeNode> generateTrees(int n) {
if(n==0)
return new ArrayList<TreeNode>();
return generateTrees(1,n);
}
private List<TreeNode> generateTrees(int start, int end) {
// TODO Auto-generated method stub
List<TreeNode> allList=new ArrayList<TreeNode>();//返回start-end的所有可能的节点
if(start>end)//要有null
{
allList.add(null);
return allList;
}
for(int i=start;i<=end;i++)
{
List<TreeNode>leftNodes=generateTrees(start,i-1);//左侧
List<TreeNode>rightNodes=generateTrees(i+1,end);//右侧
for(TreeNode lnode:leftNodes)
{
for(TreeNode rNode:rightNodes)//进行组合
{
TreeNode node=new TreeNode(i);
node.left=lnode;
node.right=rNode;
allList.add(node);//创建新节点添加到集合中
}
}
}
return allList;
}
原创不易,bigsai请你帮两件事帮忙一下:
-
star支持一下, 您的肯定是我在平台创作的源源动力。
-
微信搜索「bigsai」,关注我的公众号,不仅免费送你电子书,我还会第一时间在公众号分享知识技术。加我还可拉你进力扣打卡群一起打卡LeetCode。
记得关注、咱们下次再见!
