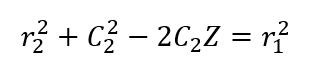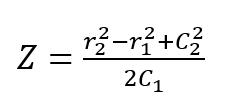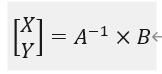优化三维空间定位法及C语言快捷实现
一、三维空间定位原理
假设我们知道自身到定位基站的距离di (i=1 2 3 4…)并且知道定位基站的坐标,那么我们就可以在空间上建立n个以基站坐标为圆心,距离为半径的空间球体,球体方程如下。其中a,b,c为基站坐标,r为被定位者距离基站的绝对距离。
假定,我们拥有三个定位基站,那么我们就可以得到一个方程组。该方程组最终可以解得两组实数数据。此时高度无法准确的确定,如果要确定准确的高度,我们就要在引入一个基站,构成一个拥有四个方程的方程组。解这个方程组就可以得到我们想要的坐标了。
但是这里就会产生一个问题:使用单片机解一个含有三个参数的二元二次方程组显然这样做不太方面,而且如果被定位者过多或基站过多就会导致坐标更新延迟等问题。所以笔者基于这一问题对计算进行优化处理。
二、定高
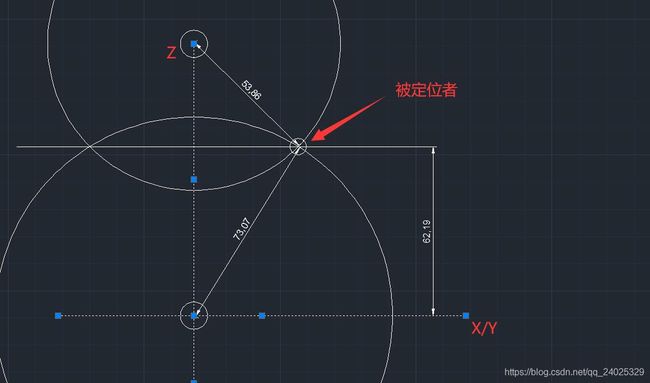
首先我们先检测被定位者的相对高度。这里设置两个基站A和B,它们的坐标只有Z轴不同,即一上一下两个基站如图所示,此时空间两个球体相交与空间一个一个空间平面,并且该平面平行于绝对平面(地面)。故我们只需要考虑该平面的高度即可
此时我们得到简化后的方程组为
化简后联立得
此时高度为
三、空间定位到平面定位
在第二节我们已经使用了两个基站,并得到了被定位者的高度。这里我们在设置两个基站C和D,并保证C和D与A或B在同一平面。然后我们将被定位者的坐标,利用第二节得到的高度投影到ACD所在的平面,这样我们就可以将空间坐标转换到平面来进行计算,即不在考虑Z轴的问题。此时我们列出两个方程
化简联立方程组,消去XY的平方项得到方程a
该方程的物理意义及为两圆在平面中相交所得到的平面直线。同理化简并联立1 3 得到方程 b
综上方程a和方程b我们可以写成矩阵的形式如下
四、验证
这里笔者先使用了CAD绘制了一个坐标,再使用MATLAB进行计算和验证。
clear
clc
A = [0 0];
B = [100 0];
C = [0 100];%定义坐标
La = 70;
Lb = 74.17;
Lc = 67.86;%定义基站距定位点距离
D = [2*A(1)-2*B(1) 2*A(2)-2*B(2);
2*A(1)-2*C(1) 2*A(2)-2*C(2)]; %定义参数矩阵
XY = [0;
0];
Z = [(Lb^2 - La^2)+(A(1)^2 - B(1)^2)+(A(2)^2 - B(2)^2);
(Lc^2 - La^2)+(A(1)^2 - C(1)^2)+(A(2)^2 - C(2)^2)];
XY = D^-1 * Z
%%===========运行结果==============%%
XY =
46.9941
51.4751
五、使用C语言实现
采用C语言实现主要是需要用C语言做矩阵的逆和矩阵乘法,具体代码如下
//================计算矩阵的逆================//
#include
#define N 10
double Det(double arcs[N][N],int n)//按第一行展开计算|A|
{
double ans = 0;
double temp[N][N];
int i,j,k;
double t;
if(n==1)
{
return arcs[0][0];
}
for(i=0;i=i)?k+1:k];
}
}
t = Det(temp,n-1);
if(i%2==0)
{
ans += arcs[0][i]*t;
}
else
{
ans -= arcs[0][i]*t;
}
}
return ans;
}
void Minor(double arcs[N][N],double ans[N][N],int n)//计算每一行每一列的每个元素所对应的余子式,组成A*
{
int i,j,k,t;
double temp[N][N];
if(n==1)
{
ans[0][0] = 1;
return;
}
for(i=0;i=i?k+1:k][t>=j?t+1:t];
}
}
ans[j][i] = Det(temp,n-1);
if((i+j)%2 == 1)
{
ans[j][i] = - ans[j][i];
}
}
}
}
int main()
{
double A[N][N] = {
{-200,0},{0,-200}};
double iA[N][N];
int i,j;
double dA;
dA = Det(A,2);
Minor(A,iA,2);
for(i=0;i<2;++i)
{
for(j=0;j<2;++j)
{
printf("%f ", A[i][j]);
}
printf("\n");
}
printf("\n");
for(i=0;i<2;++i)
{
for(j=0;j<2;++j)
{
printf("%f ",(iA[i][j]/dA));
}
printf("\n");
}
return 0;
} //=======================矩阵乘法===================//
#include "stdio.h"
void main()
{
double Max1[2][2]={
{7,8},{1,5}};
double Max2[2][1]={
{0.5},{0.3}};
double Max3[2][1];
unsigned char i,j;
double ans=0;
for(i=0;i<2;i++)
{
for(j=0;j<2;j++)
{
ans += Max1[i][j]*Max2[j][0];
}
Max3[i][0] = ans;
ans = 0;
}
for(i=0;i<2;i++)
{
for(j=0;j<1;j++)
{
printf("%f ",Max3[i][j]);
}
printf("\n");
}
}