【人工智能】遗传算法解决N皇后问题之Java实现

1.原理     

 遗传算法（Genetic Algorithm）类似于爬山法（Hill-climbing Search)，是一种局部束搜索算法（Local Beam Search）。GA模拟自然界的生成法则，实行优胜劣汰，偶然变异。爬山法可以看成是无性繁殖，而遗传算法可以看成是有性繁殖（两个体繁殖2新的2个体）。

遗传算法包括以下几个步骤：

（1）种群（Population）：随机生成种群。

（2）计算每个个体（Individual，有时也称为染色体Chromosome）的适应度（Fitness）。

（3）根据适应度，计算每个个体占整个种群的适应度百分比（即：个体适应度*100/种群所有个体适应度之和），我的理解是这个百分比可以根据种群大小适当放大。

（4）繁殖或交叉（Crossover）：根据上面的百分比，使用一种随机选择算法如轮盘赌法选择一对个体进行等量繁殖（Reproduction），这里面很重要的一条是要进行优胜劣汰，对于适应度最好的个体可以直接进入下一代种群，而对最差的个体直接使用最好的个体进行替代，以保证种群大小不变（个人理解）。

（5）变异（mulation）：繁殖后的个体以极小的概率进行变异

总之，遗传算法应经历以下阶段：编码（对问题进行分析，使用二进制、浮点数、十进制等方法进行编码，每一个码就是一个基因）、生成种群、计算适应度、繁殖、变异，直到找到目标状态，最后进行解码。

2.N皇后问题之遗传算法

可以将N皇后问题编码为二进制或十进制，这里以十进制为例，如8皇后的一种状态可表示为一个数组：24748552，其适应度可以用不冲突的皇后对数来度量，该个体的适应度为24，显然对于8皇后问题，如果其适应度为$(8-1)*8/2=28$就表示找到一个解。在交叉的时候可以随机选择一个位置来交叉前后部分，假设有两个个体24748552、32752411，若以第4位来交叉，则新生成的个体为：32758552、24742411，当然也可以选择某个范围或某几个范围的交叉（一般应设置变异率，值为0.7-0.99）。在变异时，随机生成一个概率，若小于预设的变异概率（一般为0.001-0.01），则进行变异，如个体24742411的第7位变异为3，则突变为24742431。

3.N皇后问题的表示

数据结构包括：种群数组（d[DSIZE][SIZE]）、列线数组（col[DSIZE][SIZE]）、主对角线数组（pdiag[DSIZE][SIZE]）、副对角线数组(cdiag[DSIZE][SIZE])、适应度数组（f[DSIZE]）、适应度百分比数组（fp[DSIZE]），其中DSIZE表示种群大小，而SIZE表示皇后个数。

import java.util.Random;
import java.util.Date;
import java.util.Queue;
//import java.util.LinkedList;
//import java.io.FileWriter;
//import java.io.BufferedWriter;
//import java.io.IOException;

public class nQueen {
    final static int SIZE=1000;//皇后数
	final static int DSIZE=100;//种群大小
	final static int MP=512;//变异率
         //种群
	static int[][] d=new int[DSIZE][SIZE];
	//col[i]表示第i列有几个皇后 
	static int[][] col=new int[DSIZE][SIZE];
	//pdiag[i]表示第i根主对角线（principal diagonal）皇后个数（从左上到右下的线） 
	static int[][] pdiag=new int[DSIZE][SIZE*2];
	//cdiag[i]表示第i根副对角线（counter diagonal）皇后个数（从右上到左下的线） 
	static int[][] cdiag=new int[DSIZE][SIZE*2];
	//适应度
	static int[] f=new int[DSIZE];;
	//适应度百分比
	static int[] fp=new int[DSIZE];

4.初始化种群

为了提高种群的质量，每行每列生成唯一的皇后，使用了isHas函数判断是否在某列上已生成皇后（当然也可以采取通用的对角线赋值加随机交换办法）。生成种群后应计算三条线（主副对角线、列线，此时列线当然都为0）上的皇后个数。

public static boolean isHas(int[] t,int k)
{
	for(int i=0;imax) max=f[i];
 	}
	//采用一种办法计算适应度百分比：fi=s-max+fi-min
	//可以稍微放大每个范围，不至于拥堵在一处
	int sum=0;
	//System.out.println("max="+max+",min=,"+min);
	//System.out.print("min="+min+"fp1:[");
	for(int i=0;i

5.交叉或变异时的调整个体

交叉或变异时，需要调整个体，这时不宜重新去生成三条线，适当调整即可。

//调整第d1个体（个体，即一种N皇后摆法）
//将其第row行皇后调整到第newcol列
public static void adjust(int d1,int row,int newCol)
{	//原第row行皇后所在列位置
	int oldCol=d[d1][row];
	if(oldCol==newCol) return;
	//列上增加值，下面三条语句可以进行相应推导而得
	f[d1]+=(col[d1][oldCol]-col[d1][newCol]-1);
	//主对角线上增加值 
    f[d1]+=(pdiag[d1][row-oldCol+SIZE-1]-pdiag[d1][row-newCol+SIZE-1]-1);
	//副对角线上增加值  
	f[d1]+=(cdiag[d1][row+oldCol]-cdiag[d1][row+newCol]-1); 
	//原列线，主副对角线都减1
	col[d1][oldCol]--;
	pdiag[d1][row-oldCol+SIZE-1]--;
	cdiag[d1][row+oldCol]--;
	//现列线，主副对角线都加1
	col[d1][newCol]++;
	pdiag[d1][row-newCol+SIZE-1]++;
	cdiag[d1][row+newCol]++;
}

6.轮盘赌算法

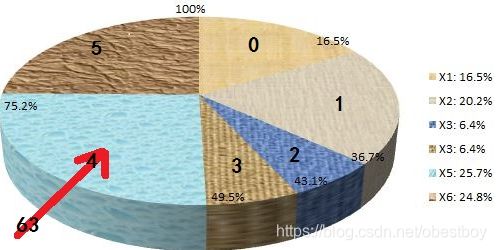
如下图所示，假设根据适应度随机选择生成了一个数为63，这时所处的范围为49.5-75.2（这个百分比是累加的），根据预设的规则应选择4。对于皇后个数很多的情况，如超过10000，建议使用二分法查找以加快查找速度。

图1 轮盘赌选择法

//轮盘赌选择一个个体（个体，即一种N皇后摆法）
public static int roulette()
{
    Date dd=new Date();
	Random r1=new Random();
	//增强随机数生成，以免一个时间点生成的都是一个数
	Random r=new Random(dd.getTime()+r1.nextLong());
	//随机生成一个概率，放大的...
	int p=r.nextInt(10000);
	if(p==0 || p=fp[i-1]) return i;
	}
	return 0;
}

7.繁殖或杂交

//杂交,第d1个与第d2个杂交
public static void crossover(int d1,int d2)
{
    Date dd=new Date();
    Random r1=new Random(dd.getTime());
    Random r=new Random(r1.nextLong()+dd.getTime());
    //随机生成一个杂交起始点与终止点
    //这对皇后个数很多比较好
    int cp1=r.nextInt(SIZE);
    int cp2=cp1+r.nextInt(SIZE-cp1);
    for(int k=cp1;k

8.变异

//变异，第d1个可能的变异
public static void mulation(int d1)
{
    Random r=new Random();
    //随机生成一个数与变异率MP（变异率）比较
    int p=r.nextInt(10000);
    if(p<=MP)
    {
    	//随机生成1个变异点
    	int mp=r.nextInt(SIZE);
    	//随机生成1个变异值
    	int mv=r.nextInt(SIZE);
        //调整三条线
    	adjust(d1,mp,mv);
    	d[d1][mp]=mv;
    }
}

9.重新计算适应度百分比

//为轮盘赌选择法计算适应度百分比
public static void perFitness()
{
    int min=f[0],max=f[0];
    int sum=0;
    int s=SIZE*(SIZE-1)/2;
    //找到最大、最小
    for(int i=0;imax) max=f[i];
    }
    //放大范围
    for(int i=0;i

10.优胜劣汰

//最好的个体直接进入下一代,最差的淘汰
public static void bestBadOperation(int c)
{
    int best=0,bad=0;
    //int maxFitness=SIZE*(SIZE-1)/2;
    int sum=0;
    for(int i=0;if[best]) best=i;
    	if(f[i]

11.遗传算法的实现

//N皇后遗传算法
//不考虑迭代次数限制！
public static int geneticAlgorithms()
{
    int c=0;//迭代次数
    //N皇后最大适应度
    int maxFitness=SIZE*(SIZE-1)/2;
    while(true)
    {
    	c++;
    	int k=0;//个体计数器
    	while(k

12.测试、结果

	public static void main(String[] args) {
		int c=0;
		int avg=0;
		int k=0;
        //测试10次取平均
		while(c<10)
		{
			c++;
			d=new int[DSIZE][SIZE];
			col=new int[DSIZE][SIZE];
			pdiag=new int[DSIZE][2*SIZE];
			cdiag=new int[DSIZE][2*SIZE];
			f=new int[DSIZE];
			fp=new int[DSIZE];
			initPopulation();
			long t1=new Date().getTime();
		    int x=geneticAlgorithms();
		    long t2=new Date().getTime();
		    avg+=(t2-t1);
		    k+=x;
		    System.out.println(c+". 耗时："+(t2-t1)+"，迭代次数："+x);
		}
		System.out.println("平均耗时："+avg/10+"，平均迭代次数："+k/10);
          //下面代码主要是将数据写到文件里，以便可以使用excel作图
		//long t1=new Date().getTime();
	    //int k=geneticAlgorithms();
	    //long t2=new Date().getTime();
	    //System.out.println(k+":");
	    
	    /*Iterator it=itQueue.iterator();
	    Iterator itBest=bestQueue.iterator();
	    Iterator itBad=badQueue.iterator();
	    Iterator itAvg=avgQueue.iterator();*/
	    /*try {
	       FileWriter fw=new FileWriter("100.txt",false); 
	       BufferedWriter bw=new BufferedWriter(fw);
	    
	       while(!itQueue.isEmpty())
	       {
	    	   bw.newLine();
	    	   bw.write(itQueue.poll()+","+bestQueue.poll()+","+badQueue.peek()+","+avgQueue.poll());
	       }
	       bw.close();
	       fw.close();
	    }
	    catch(IOException e)
	    {
	    	System.out.println(e.getMessage());
	    }*/
	   // for(int j=0;j

遗传算法是随机算法，每次执行的性能都不一样，以10次计算其平均得到以下数据。可以看出，随着种群规模的增加，所花费的时间代价变大，但同时迭代次数降低。

表1 不同皇后数不同种群数遗传算法代价

皇后个数	种群大小	迭代次数	平均耗时	变异率
100	8	281759	1185	512
100	32	135129	1992	512
100	64	103985	3155	512
100	100	57096	6015	512
100	200	83171	8937	512
皇后个数	种群大小	迭代次数	平均耗时	变异率
200	8	1089878	5597	512
200	32	682308	12140	512
200	64	364283	11967	512
200	100	328676	19302	512
200	200	253067	29309	512
皇后个数	种群大小	迭代次数	平均耗时	变异率
500	8	4328368	36747	512
500	32	2337116	63851	512
500	64	1593558	69508	512
500	100	1574437	112037	512
500	200	2016290	312787	512
皇后个数	种群大小	迭代次数	平均耗时	变异率
1000	100	4248935	447166	512
2000	100	17572171	2762050	512

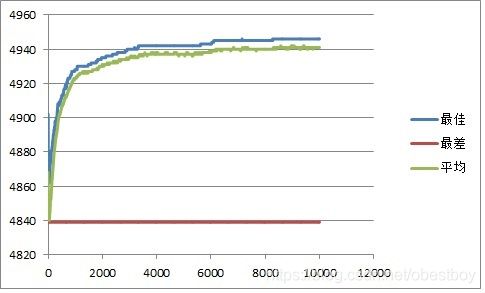
下图是100皇后迭代10000次的结果，其中横轴表示迭代次数，纵轴表示适应度值。可以看到，刚开始时，遗传算法迅速变好，最后缓慢变化并趋于稳定（或收敛）。最差个体几乎没什么变化，而最佳个体与平均适应度变化趋势趋同。

图2 100皇后、种群100个，迭代10000次

13.结论及问题

传算法应该比爬山法慢，尤其是在种群数量比较大的情况下，但是遗传算法可以使用模式（Schemata）来加速目标个体的形成。模式就是一种匹配方式，对于一些明显的不符合要求的可以过滤掉，如对N皇后问题可以使用构造法生成一些匹配模式。由于遗传算法加入了变异功能，一般来说，对于一个问题总能找到其解。但是在本程序里，由于优胜劣汰算法可能不够好，最后除了那些变异的外，其余全部都是一样的。之所以都能找到解，是因为在收敛成一样后进行了变异，这相当于在进行随机全局搜索，因此迭代的次数很多。像100皇后的100种群，基本在4000次迭代后就只是变异在起作用。另外一个问题是，遗传算法必须要有优胜劣汰机制，否则无法快速收敛到一个较好的水平。正如前面所述，优胜劣汰机制也导致最终全部个体都一样。这显然不符合自然法则，个体的多样性没有得到保证。期待有时间更深入去探索遗传算法。