12.21-12.27
[103. 二叉树的锯齿形层序遍历]
题目描述
给定一个二叉树,返回其节点值的锯齿形层序遍历。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
例如:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回锯齿形层序遍历如下:
[
[3],
[20,9],
[15,7]
]
DFS
使用dfs,对应层判断一下奇偶,决定在表头还是表尾添加元素就可以了
Code
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
traversal(root, res, 0);
return res;
}
private void traversal(TreeNode root,List<List<Integer>> res,int level){
if(root == null){
return;
}
if(res.size() == level){
res.add(new ArrayList<Integer>());
}
if((level & 1) == 1){
res.get(level).add(0,root.val);//是奇数层则在表头加入
}else{
res.get(level).add(root.val);//偶数层在表尾加入
}
traversal(root.left,res,level+1);
traversal(root.right,res,level+1);
}
}
队列BFS
用队列来暂时存储节点,在bfs时先统计这一层的节点数量,然后再根据节点数量选择表头加入还是表尾加入
Code
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
if (root == null) {
return Collections.emptyList();
}
LinkedList<TreeNode> queue = new LinkedList<>();
queue.add(root);
List<List<Integer>> res = new ArrayList<>();
boolean reverse = true;
while (queue.size() > 0) {
List<Integer> tmp = new ArrayList<>(queue.size());
for (int i = queue.size() - 1; i >= 0; i--) {
TreeNode tmpNode = reverse ? queue.removeFirst() : queue.removeLast();
tmp.add(tmpNode.val);
if (reverse) {
if (tmpNode.left != null) {
queue.addLast(tmpNode.left);
}
if (tmpNode.right != null) {
queue.addLast(tmpNode.right);
}
} else {
if (tmpNode.right != null) {
queue.addFirst(tmpNode.right);
}
if (tmpNode.left != null) {
queue.addFirst(tmpNode.left);
}
}
}
res.add(tmp);
reverse = !reverse;
}
return res;
}
}
[746. 使用最小花费爬楼梯]
题目描述
数组的每个索引作为一个阶梯,第 i个阶梯对应着一个非负数的体力花费值 cost[i](索引从0开始)。
每当你爬上一个阶梯你都要花费对应的体力花费值,然后你可以选择继续爬一个阶梯或者爬两个阶梯。
您需要找到达到楼层顶部的最低花费。在开始时,你可以选择从索引为 0 或 1 的元素作为初始阶梯。
示例 1:
输入: cost = [10, 15, 20]
输出: 15
解释: 最低花费是从cost[1]开始,然后走两步即可到阶梯顶,一共花费15。
示例 2:
输入: cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1]
输出: 6
解释: 最低花费方式是从cost[0]开始,逐个经过那些1,跳过cost[3],一共花费6。
(动态规划)
这个爬楼梯的问题和斐波那契数列问题很像。
读完题大家应该知道指定需要动态规划的,贪心是不可能了。
然后我们按照动规四步曲:
1.确定dp数组以及下标的含义
1.1:使用动态规划,就要有一个数组来记录状态,本题只需要一个一维数组dp[i]就可以了。
1.2:dp[i]的定义:第i个台阶所花费的最少体力为dp[i]。
2.确定递推公式
2.1可以有两个途径得到dp[i],一个是dp[i-1] 一个是dp[i-2]。
那么究竟是选dp[i-1]还是dp[i-2]呢?
2.2:一定是选最小的,所以dp[i] = min(dp[i - 1], dp[i - 2]) + cos:t[i];
注意这里为什么是加cost[i],而不是cost[i-1],cost[i-2]之类的,因为题目中说了:第i个阶梯对应着一个非负数的体力花费值 cost[i]
3.dp数组如何初始化
3.1:根据dp数组的定义,dp数组初始化其实是比较难的,因为不可能初始化为第i台阶所花费的最少体力。
3.2:那么看一下递归公式,dp[i]由dp[i-1],dp[i-2]推出,既然初始化所有的dp[i]是不可能的,那么只初始化dp[0]和dp[1]就够了,其他的最终都是dp[0],dp[1]推出。
4.确定遍历顺序
4.1:因为是模拟台阶,而且dp[i]又dp[i-1]dp[i-2]推出,所以是从前到后遍历cost数组就可以了。
Code
class Solution {
public int minCostClimbingStairs(int[] cost) {
int[] dp = new int[cost.length];
dp[0] = cost[0];
dp[1] = cost[1];
for(int i = 2; i<cost.length; i++){
dp[i] = Math.min(dp[i-1],dp[i-2])+cost[i];
}
return Math.min(dp[cost.length - 1],dp [cost.length - 2]);
}
}
[387. 字符串中的第一个唯一字符]
题目描述
给定一个字符串,找到它的第一个不重复的字符,并返回它的索引。如果不存在,则返回 -1。
示例:
s = "leetcode"
返回 0
s = "loveleetcode"
返回 2
建立map数组
创建一个长度为26的数组,每一个下标对应一个字母,当读取到该字母时,则这个下标++,最后从头开始遍历数组,当找到第一个下标值为1的字母时,return其下标
Code
class Solution {
public int firstUniqChar(String s) {
int[] map = new int[26];
char[] chars = s.toCharArray();
for (char c : chars) {
map[c - 'a']++;
}
for (int i = 0; i < chars.length; i++) {
if (map[chars[i] - 'a'] == 1)
return i;
}
return -1;
}
}
HashMap
相当于上一种办法的详细版,建立每个char ch与 它所出现次数count的map映射关系,然后遍历map,找到第一个count为1的char,将其return掉
Code
class Solution {
public int firstUniqChar(String s) {
Map<Character, Integer> map = new HashMap<>(26);
char[] chars = s.toCharArray();
for (char ch : chars) {
map.put(ch, map.getOrDefault(ch, 0) + 1);
}
for (int i = 0; i < chars.length; i++) {
if (map.get(chars[i]) == 1) {
return i;
}
}
return -1;
}
}
indexOf和lastIndexOf
调用系统库函数indexOf和lastIndexOf(),如果两者相等,则说明这个字符只出现了一次,将其return掉
Code
class Solution {
public int firstUniqChar(String s){
char[] chars = s.toCharArray();
int len = chars.length;
if(len == 1){
return 0;
}
for (int i = 0; i < len; i++) {
if(s.indexOf(chars[i]) == s.lastIndexOf(chars[i])){
return i;
}
}
return -1;
}
}
[135. 分发糖果]
题目描述
老师想给孩子们分发糖果,有 N 个孩子站成了一条直线,老师会根据每个孩子的表现,预先给他们评分。
你需要按照以下要求,帮助老师给这些孩子分发糖果:
每个孩子至少分配到 1 个糖果。
相邻的孩子中,评分高的孩子必须获得更多的糖果。
那么这样下来,老师至少需要准备多少颗糖果呢?
示例I/O
输入: [1,0,2]
输出: 5
解释: 你可以分别给这三个孩子分发 2、1、2 颗糖果。
输入: [1,2,2]
输出: 4
解释: 你可以分别给这三个孩子分发 1、2、1 颗糖果。
第三个孩子只得到 1 颗糖果,这已满足上述两个条件。
贪心(两次遍历)
这种题目是很典型的贪心算法,一定是要确定一边之后,再确定另一边,例如比较每一个孩子的左边,然后再比较右边,如果两边一起考虑就会顾此失彼。先初始化一个糖果数组candyArray用来记录每位孩子应该得到的糖果数并全部赋值为1。
先从前往后遍历,如果后一个孩子的得分比前一个高,则比前一个孩子多得到一颗糖果
再从后往前遍历,如果前一个孩子的得分比后一个孩子得分高,那么就看前一个孩子所得糖果数量和后一个孩子的糖果数+1哪个更大,选择更大的作为前一个孩子所得糖果数
Code
class Solution {
public int candy(int[] ratings) {
int len = ratings.length;
if(len == 0 || ratings == null){
return 0;
}
if(len == 1){
return 1;
}
//初始化糖果数组
int[] candyArray = new int[len];
Arrays.fill(candyArray,1);
//从前往后
for (int i = 1; i < len; i++) {
if(ratings[i] > ratings[i - 1]){
candyArray[i] = candyArray[i - 1] + 1;
}
}
//从后往前
for (int i = len - 2; i >= 0; i--) {
if(ratings[i] > ratings[i + 1]){
candyArray[i] = Math.max(candyArray[i],candyArray[i + 1] + 1);
}
}
//求和
int result = 0;
for (int i : candyArray) {
result += i;
}
return result;
}
}
[85. 最大矩形]
题目描述:
给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
示例 1:
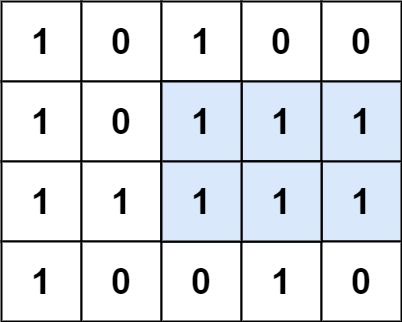
输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出:6
解释:最大矩形如上图所示。
示例 2:
输入:matrix = []
输出:0
示例 3:
输入:matrix = [["0"]]
输出:0
示例 4:
输入:matrix = [["1"]]
输出:1
示例 5:
输入:matrix = [["0","0"]]
输出:0
(动态规划)
有点类似暴搜,先处理边界,然后依次遍历每个点,找到最小宽度然后乘以高度即可
Code
class Solution {
public int maximalRectangle(char[][] matrix) {
int m = matrix.length;
if (m == 0) {
return 0;
}
int n = matrix[0].length;
// 记录每个点的最大宽(向左的连续1长度)和最大高(向上的连续1长度)
int[][][] dp = new int[m][n][2];
int res = 0;
// 左上角
if (matrix[0][0] == '0') {
dp[0][0][0] = 0;
dp[0][0][1] = 0;
}
else {
dp[0][0][0] = 1;
dp[0][0][1] = 1;
res = 1;
}
// 最左1列
for(int i = 1; i < m; i ++) {
if (matrix[i][0] == '0') {
dp[i][0][0] = 0;
dp[i][0][1] = 0;
}
else {
dp[i][0][0] = 1;
dp[i][0][1] = 1 + dp[i - 1][0][1];
res = Math.max(res, dp[i][0][1]);
}
}
// 最上1行
for (int j = 1; j < n; j ++) {
if (matrix[0][j] == '0') {
dp[0][j][0] = 0;
dp[0][j][1] = 0;
}
else {
dp[0][j][0] = 1 + dp[0][j - 1][0];
dp[0][j][1] = 1;
res = Math.max(res, dp[0][j][0] * 1);
}
}
for (int i = 1; i < m; i ++) {
for (int j = 1; j < n; j ++) {
if (matrix[i][j] == '1') {
dp[i][j][0] = dp[i][j - 1][0] + 1;
dp[i][j][1] = dp[i - 1][j][1] + 1;
// 需要保证围成的矩形只包含1
// 向左遍历判断最大矩形的高能否是height
int height = dp[i][j][1];
while (height > 0) {
for (int y = j - 1; y >= 0; y --) {
if (dp[i][y][1] < height) {
break;
}
else {
res = Math.max(res, (j - y + 1) * height);
}
}
height --;
}
// 向上遍历判断最大矩形的宽能否是width
int width = dp[i][j][0];
while (width > 0) {
for (int x = i - 1; x >= 0; x --) {
if (dp[x][j][0] < width) {
break;
}
else {
res = Math.max(res, (i - x + 1) * width);
}
}
width --;
}
}
}
}
return res;
}
}
[剑指 Offer 10- I. 斐波那契数列]
题目描述:
写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项。斐波那契数列的定义如下:
F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
斐波那契数列由 0 和 1 开始,之后的斐波那契数就是由之前的两数相加而得出。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
示例I/O
输入:n = 2
输出:1
输入:n = 5
输出:5
(动态规划)
这题我先用了递归,后来爆表了...
后来试了动态规划,才可以AC,感觉这种题目都只能用动态规划来做才不会爆表...
题目已经给了动态规划方程F(N) = F(N-1)+F(N-2)
边界条件为dp[0] = 0,dp[1] = 1,执行dp之前判断一下即可
所以用上这个规划条件即可
Code
class Solution {
public int fib(int n) {
if(n < 2){
return n;
}
int[] dp = new int[n + 1];
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] =(dp[i-1] + dp[i-2]) % 1000000007;
}
return dp[n];
}
}
[1025. 除数博弈]
题目描述:
爱丽丝和鲍勃一起玩游戏,他们轮流行动。爱丽丝先手开局。
最初,黑板上有一个数字 N 。在每个玩家的回合,玩家需要执行以下操作:
选出任一 x,满足 0 < x < N 且 N % x == 0 。
用 N - x 替换黑板上的数字 N 。
如果玩家无法执行这些操作,就会输掉游戏。
只有在爱丽丝在游戏中取得胜利时才返回 True,否则返回 False。假设两个玩家都以最佳状态参与游戏。
示例I/O
示例 1:
输入:2
输出:true
解释:爱丽丝选择 1,鲍勃无法进行操作。
示例 2:
输入:3
输出:false
解释:爱丽丝选择 1,鲍勃也选择 1,然后爱丽丝无法进行操作。
数学方法
有一个原则就是先手偶数必胜。先手为偶数的话,先手只需要让自己每步都保持偶数,那么他可以通过让对手得到的数为奇数,比如偶数-1就是奇数了,对手拿到奇数,那么能整除的只有奇数,奇数-奇数又回到了偶数,最后先手一定会得到最小的偶数2,然后-1让对手得到1,对手无解,必胜。
Code
class Solution {
public boolean divisorGame(int N) {
return N%2==0;
}
}
(动态规划)
基本思路:
将所有的小于等于 N 的解都找出来,基于前面的,递推后面的。
状态转移: 如果 i 的约数里面有存在为 flase 的(即输掉的情况),则当前 i 应为 true;如果没有,则为 false。
Code
class Solution {
public boolean divisorGame(int N){
if(N == 1){
return false;
}
if(N == 2){
return true;
}
boolean[] dp = new boolean[N+1];
dp[1] = false;
dp[2] = true;
for (int i = 3; i < N+1; i++) {
for (int j = 1; j < i; j++) {
if(i % j ==0 && dp[i - j] == false){
dp[i] = true;
break;
}
dp[i] = false;
}
}
return dp[N];
}
}
[同构字符串]
题目描述:
给定两个字符串 s 和 t,判断它们是否是同构的。
如果 s 中的字符可以被替换得到 t ,那么这两个字符串是同构的。
所有出现的字符都必须用另一个字符替换,同时保留字符的顺序。两个字符不能映射到同一个字符上,但字符可以映射自己本身。
示例I/O
示例 1:
输入: s = "egg", t = "add"
输出: true
示例 2:
输入: s = "foo", t = "bar"
输出: false
示例 3:
输入: s = "paper", t = "title"
输出: true
HashMap
这种题一般使用hashmap建立起映射关系即可,如果不存在这一组键值,那么则添加,添加前考虑value值是否唯一即可,如果已存在,则考虑新的value值是否与原value值相同
Code
class Solution {
public boolean isIsomorphic(String s, String t) {
char[] chars = s.toCharArray();
char[] chars1 = t.toCharArray();
Map<Character, Character> map = new HashMap<>(chars.length);
for (int i = 0; i < chars.length; i++) {
if(!map.containsKey(chars[i])){
if(map.containsValue(chars1[i])){
return false;
}
map.put(chars[i],chars1[i]);
}else{
if(map.get(chars[i])!=chars1[i]){
return false;
}
}
}
return true;
}
}
(数组模拟map)
创建两个数组,分别对应s->t和t->s的映射关系,然后在添加时,先看是否有,没有则插入,有则双向比较
Code1
class Solution {
public boolean isIsomorphic(String s, String t) {
int []map1=new int[256];
int []map2=new int[256];
for(int i=0;i<t.length();i++){
if(map1[(int)s.charAt(i)]==0&&map2[(int)t.charAt(i)]==0){
map1[(int)s.charAt(i)]=(int)t.charAt(i);
map2[(int)t.charAt(i)]=(int)s.charAt(i);
}else{
if(map1[(int)s.charAt(i)]!=(int)t.charAt(i)){
return false;
}
}
}
return true;
}
}
Code2
class Solution {
public boolean isIsomorphic(String s, String t) {
return canMap(s, t) && canMap(t, s);
}
private boolean canMap(String s, String t) {
if (s.length() != t.length()) {
return false;
}
int[] ms = new int[128];
char[] cs = s.toCharArray();
char[] ct = t.toCharArray();
int len = s.length();
for (int i = 0; i < len; i++) {
if (ms[cs[i]] == 0) {
ms[cs[i]] = ct[i];
} else if (ms[cs[i]] != ct[i]) {
return false;
}
}
return true;
}
}